In this video I go over equations of lines and planes in 3D coordinates. This section is part of my calculus book chapter titled Vectors and the Geometry of Space. In 2D coordinates, a line can be described by a point on the line and its slope or direction. Similarly, a line in 3D coordinates can be described by a point on the line and a vector parallel to it which thus serves as the direction. A plane in 3D coordinates is described by a point on the plane and a vector perpendicular to the plane. The plane equation utilizes the fact that the dot product of two perpendicular vectors is equal to zero. Furthermore, the cross product is also used in determining the perpendicular vector, termed a normal vector. I go through several related concepts, such as scalar and vector equations of lines, segments of lines, and linear equations of planes, as well as many examples to give a thorough examination of 3D lines and planes.
The topics covered as well as their timestamps are listed below.
- Introduction: 0:00
- Calculus Book Reference: 1:13
- Sections in Calculus Book Chapter: 1:27
- Topics to Cover: 2:28
- Lines: 3:42
- Vector Equation of a Line: 5:00
- Parametric Equations of a Line: 12:50
- Example 1: 17:22
- Solution to 1(a): 17:49
- Solution to 1(b): 25:55
- Direction Numbers: 28:08
- Symmetric Equations of a Line: 31:49
- Example 2: 37:29
- Solution to 2(a): 37:54
- Solution to 2(b): 43:43
- Note on Example 2: 48:38
- Equation of a Line Segment: 50:24
- Example 3: 1:04:16
- Planes: 1:15:15
- Vector Equation of a Plane: 1:15:32
- Scalar Equation of a Plane: 1:21:13
- Example 4: 1:23:14
- Linear Equation of a Plane: 1:29:40
- Example 5: 1:32:58
- Example 6: 1:42:27
- Parallel Planes: 1:48:18
- Example 7: 1:52:34
- Solution to 7(a): 1:52:58
- Solution to 7(b): 1:58:13
- Note 1: Two Linear Equations Can Represent a Line: 2:08:20
- Note 2: Line of Intersection from Two Parametric Planes: 2:16:18
- Example 8: Distance from a Point to a Plane: 2:19:55
- Example 9: 2:30:45
- Example 10: 2:38:04
- Exercise 1: 2:55:19
- PDF video notes: https://1drv.ms/b/s!As32ynv0LoaIiecyXiOIVbA_nizjLQ
- Video sections playlist: https://www.youtube.com/playlist?list=PLai3U8-WIK0FO3u0IupqllNNkZTsffpIV
- Vectors and the Geometry of Space video series: https://www.youtube.com/playlist?list=PLai3U8-WIK0FjJpwnxwdrOR7L8Ul8VZoZ
Watch video on:
- 3Speak:
- Odysee: https://odysee.com/@mes:8/equations-of-lines-and-planes:0
- BitChute:
- Rumble: https://rumble.com/v2ywjz0-vectors-and-the-geometry-of-space-equations-of-lines-and-planes.html
- DTube:
- YouTube:
View Video Notes Below!
Download these notes: Link is in video description.
View these notes as an article: @mes
Subscribe via email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donate
Buy MES merchandise! https://mes.fm/store
More links: https://linktr.ee/matheasy
Follow my research in real-time on my MES Links Telegram: https://t.me/meslinks
Subscribe to MES Truth: https://mes.fm/truthReuse of my videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight back against censorship:
- Bookmark sites/channels/accounts and check periodically
- Remember to always archive website pages in case they get deleted/changed.
Recommended Books:
- "Where Did the Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
Join my forums!
- Hive community: created/hive-128780
- Reddit: https://reddit.com/r/AMAZINGMathStuff
- Discord: https://mes.fm/chatroom
Follow along my epic video series:
- #MESScience: https://mes.fm/science-playlist
- #MESExperiments: @mes/list
- #AntiGravity: @mes/series
-- See Part 6 for my Self Appointed PhD and #MESDuality breakthrough concept!- #FreeEnergy: https://mes.fm/freeenergy-playlist
- #PG (YouTube-deleted series): @mes/videos
NOTE #1: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (if available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed!
-- MES tutorial: @mes/play-videos-at-faster-or-slower-speeds-on-any-website- Download and read video notes.
- Read notes on the Hive blockchain $HIVE
- Watch the video in parts.
-- Timestamps of all parts are in the description.Browser extension recommendations:
- Increase video speed: https://mes.fm/videospeed-extension
- Increase video audio: https://mes.fm/volume-extension
- Text to speech: https://mes.fm/speech-extension
--Android app: https://mes.fm/speech-android
Vectors and the Geometry of Space: Equations of Lines and Planes
Calculus Book Reference
Note that I mainly follow along the following calculus book:
- Calculus: Early Transcendentals 7th Edition by James Stewart
- Note: In the earlier videos I used the 6th edition.
Sections in Calculus Book Chapter
I have made a list of the sections in this particular chapter with links to the Hive post of the videos I have already finished.
Note that I have started splitting each long video into sections and made a playlist for each.
Vectors and the Geometry of Space
- 3-D Coordinate Systems
- Vectors
- The Dot Product
- The Cross Product
- Equations of Lines and Planes (Current Video)
- Playlist
- Laboratory Project: Putting 3D in Perspective
- Cylinders and Quadric Surfaces
- Review
- True-False Quiz
- Problems Plus
Topics to Cover
Note that the timestamps will be included in the video description for each topic listed below.
- Lines
- Vector Equation of a Line
- Parametric Equations of a Line
- Example 1
- Solution to 1(a)
- Solution to 1(b)
- Direction Numbers
- Symmetric Equations of a Line
- Example 2
- Solution to 2(a)
- Solution to 2(b)
- Note on Example 2
- Equation of a Line Segment
- Example 3
- Planes
- Vector Equation of a Plane
- Scalar Equation of a Plane
- Example 4
- Linear Equation of a Plane
- Example 5
- Example 6
- Parallel Planes
- Example 7
- Solution to 7(a)
- Solution to 7(b)
- Note 1: Two Linear Equations Can Represent a Line
- Note 2: Line of Intersection from Two Parametric Planes
- Example 8: Distance from a Point to a Plane
- Example 9
- Example 10
- Exercise 1
Lines
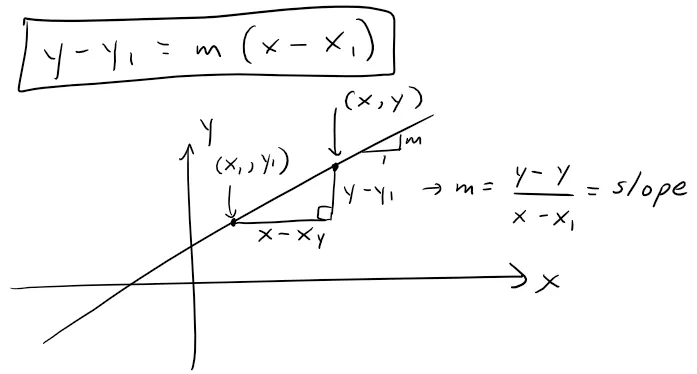
A line in the xy-plane is determined when a point on the line and the direction of the line (its slope or angle of inclination) are given.
The equation of the line can be written using the point-slope form.
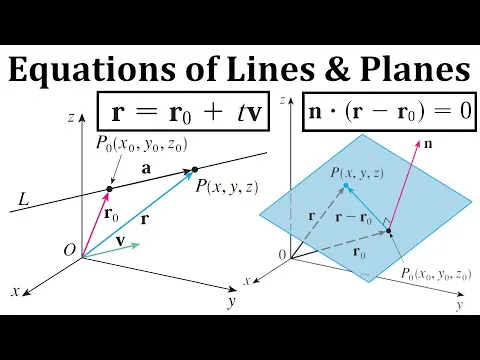
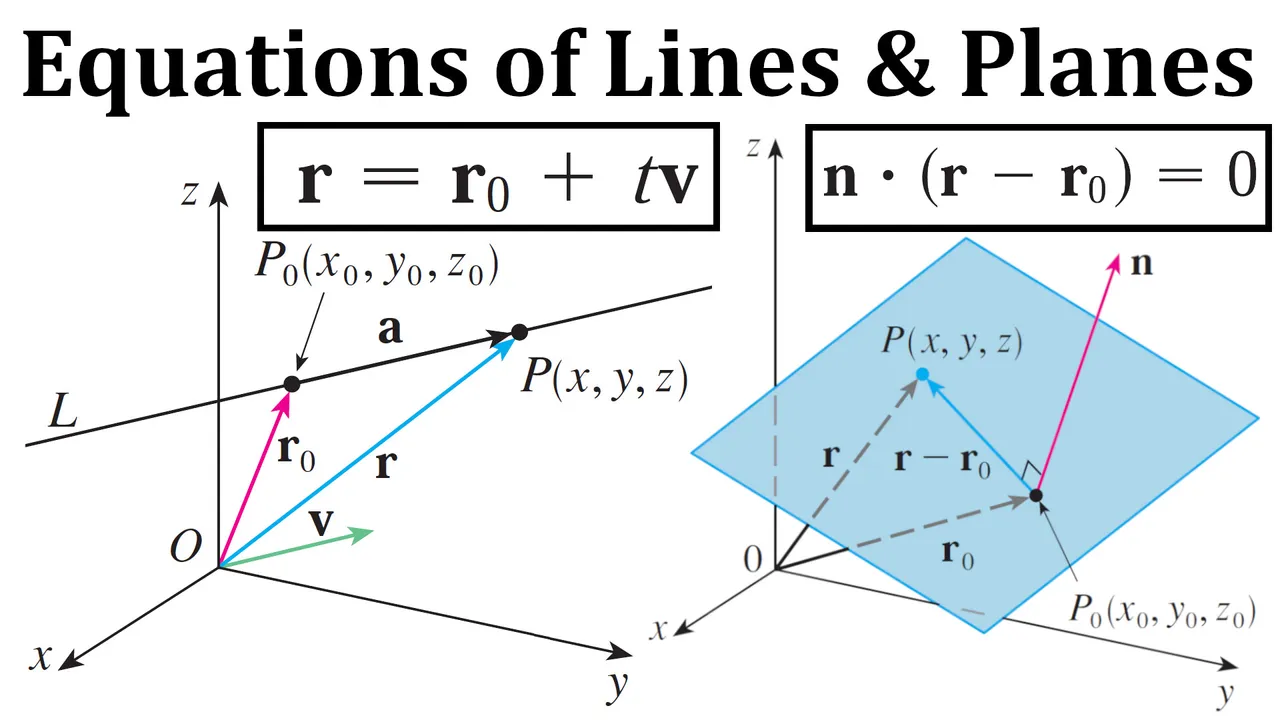
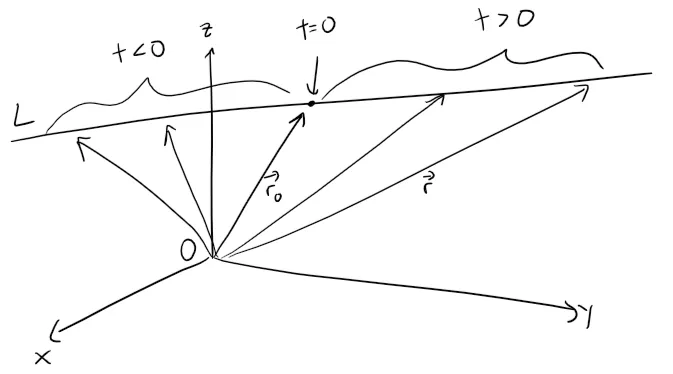
Likewise, a line L in three-dimensional space is determined when we know a point P0(x0, y0, z0) on L and the direction of L.
Vector Equation of a Line
In three dimensions the direction of a line is conveniently described by a vector, so we let v be a vector parallel to L.
Let P(x, y, z) be an arbitrary point on L and let r0 and r be the position vectors of P0 and P (that is, they have representations OP0 and OP).
If a is the vector with representation P0P, as in the figure below, then the Triangle Law for vector addition gives r = r0 + a.
But, since a and v are parallel vectors, there is a scalar t such that a = tv.
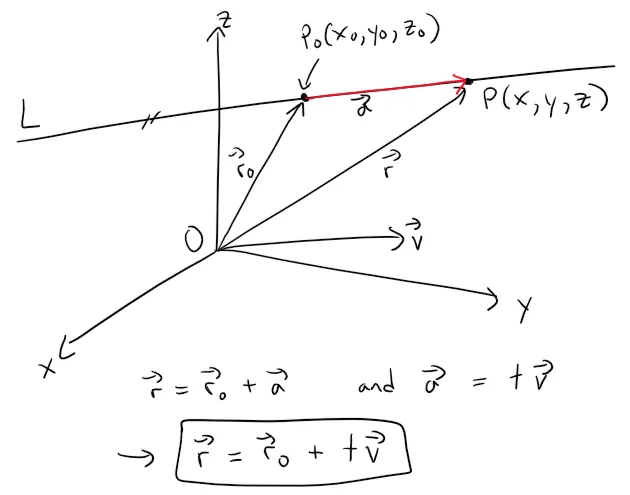
The above equation is called a vector equation of L.
Each value of the parameter t gives the position vector r of a point on L.
In other words, as t varies, the line is traced out by the tip of the vector r.
As the figure below indicates, positive values of t correspond to points on L that lie on one side of P0, whereas negative values of t correspond to points that lie on the other side of P0.
Parametric Equations of a Line
If the vector v that gives the direction of the line L is written in component form as v = <a, b, c>, then we have tv = <ta, tb, tc>.
We can also write r = <x, y, z> and r0 = <x0, y0, z0>, so the earlier vector equation becomes:
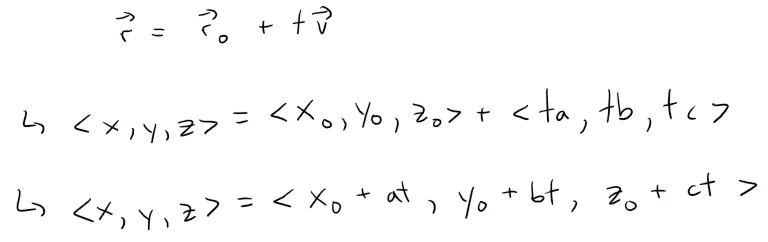
Two vectors are equal if and only if their corresponding components are equal.
Therefore we have the three scalar equations.
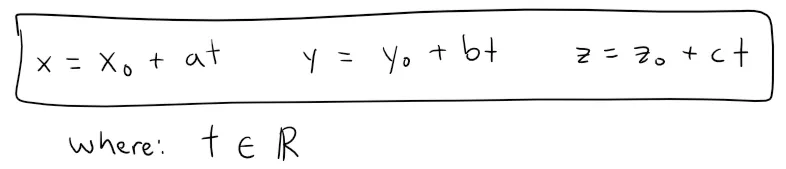
These equations are called parametric equations of the line L through the point P0(x0, y0, z0) and parallel to the vector v = <a, b, c>.
Each value of the parameter t gives a point (x, y, z) on L.
Example 1
(a) Find a vector equation and parametric equations for the line that passes through the point (5, 1, 3) and is parallel to the vector i + 4j - 2k.
(b) Find two other points on the line.
Solution to 1(a)
Let's graph out what we are given.
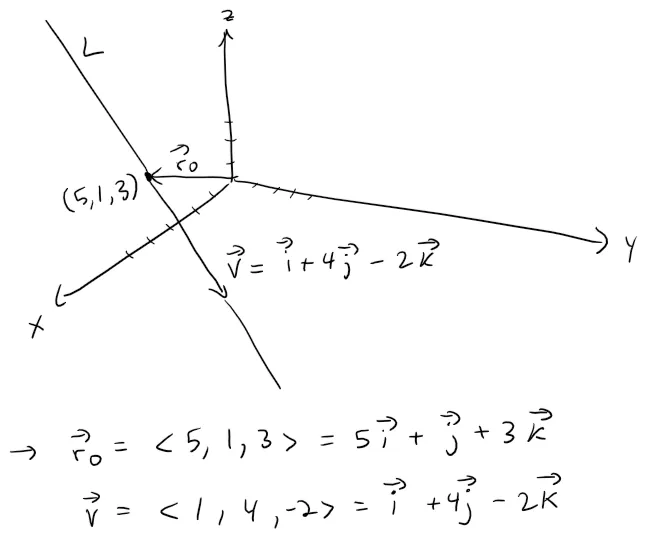
So the vector equation becomes:
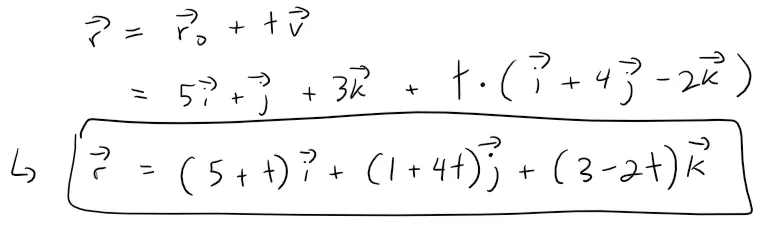
The parametric equations are:
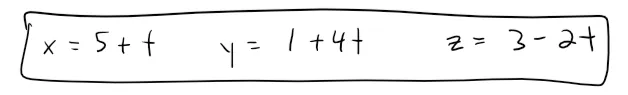
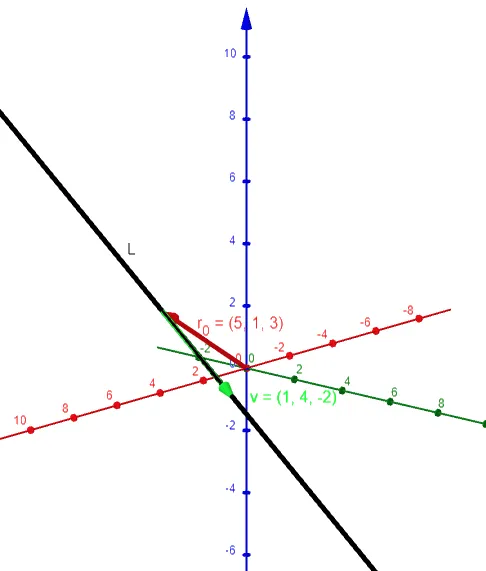
Let's double check the graph using the GeoGebra 3D graphing calculator:

Solution to 1(b)
Choosing the parameter value t = 1 gives:
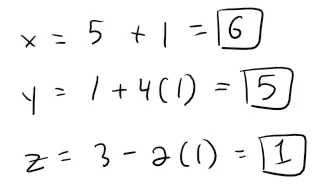
Thus (6, 5, 1) is a point on the line.
Similarly, choosing t = -1 gives the point (4, -3, 5).
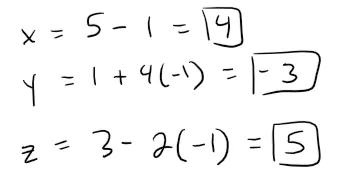
Direction Numbers
The vector equation and parametric equations of a line are not unique.
If we change a point or the parameter or choose a different parallel vector, then the equations change.
For instance, if, instead of (5, 1, 3), we choose the point (6, 5, 1) in Example 1, then the parametric equation of the line become:
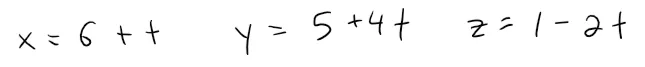
Or, if we stay with the point (5, 1, 3) but choose the parallel vector 2i + 8j - 4k, we arrive at the equations:
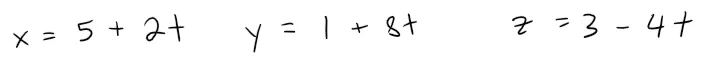
In general, if a vector v = <a, b, c> is used to describe the direction of a line L, then the numbers a, b, and c are called direction numbers of L.
Since any vector parallel to v could also be used, we see that any three numbers proportional to a, b, and c could also be used as a set of direction numbers for L.
Symmetric Equations of a Line
Another way of describing a line L is to eliminate the parameter t from the parametric equations.
If none of a, b, or c is 0, we can solve each of these equations for t, equate the results, and obtain:
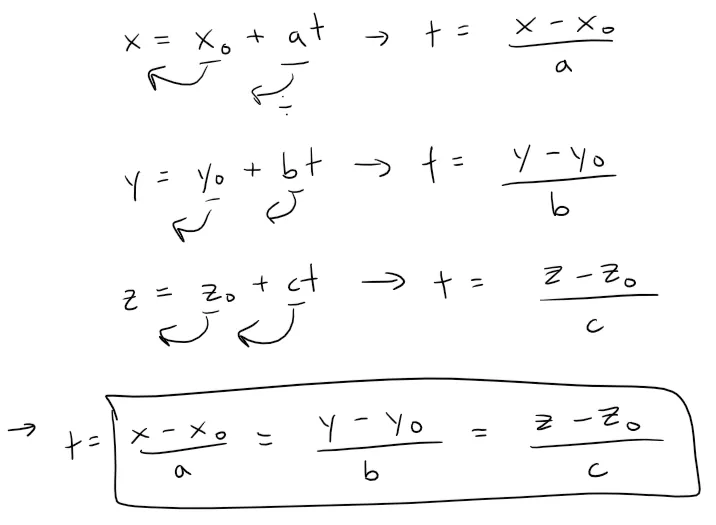
These equations are called symmetric equations of L.
Notice that the numbers a, b, and c that appear in the denominators of the equation above are direction numbers of L, that is, components of a vector parallel to L.
If one of a, b, or c is 0, we can still eliminate t.
For instance, if a = 0, we could write the equations of L as:
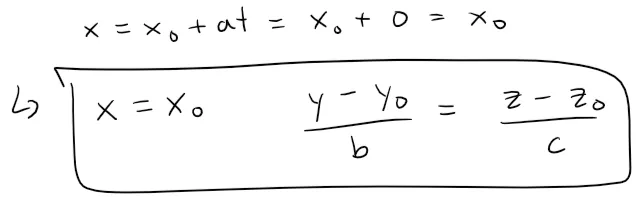
This means that L lies in the vertical plane x = x0.
Example 2
(a) Find parametric equations and symmetric equations of the line that passes through the points A(2, 4, -3) and B(3, -1, 1).
(b) At what points does this line intersect the xy-plane?
Solution 2(a)
Let's first graph out the line:
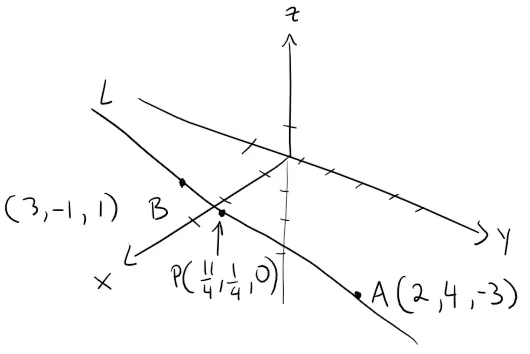
We are not explicitly given a vector parallel to the line, but observe that the vector v with representation AB is parallel to the line and:
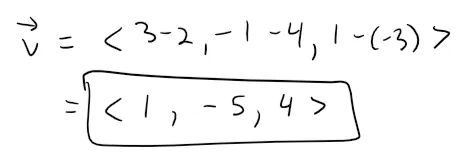
Thus the direction numbers are a = 1, b = -5, and c = 4.
Taking the point A = (2, 4, -3) as P0, we see that the parametric equations are:
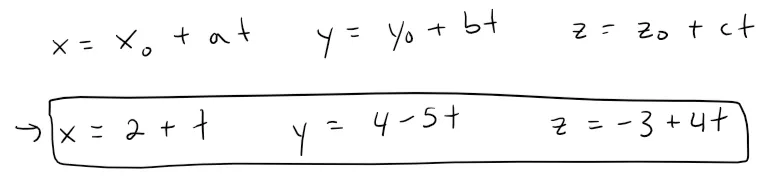
And the symmetric equations are:
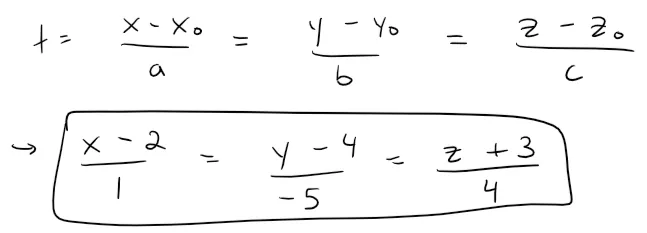
Solution to (b)
The line intersects the xy-plane when z = 0, so we put z = 0 in the symmetric equations and obtain:
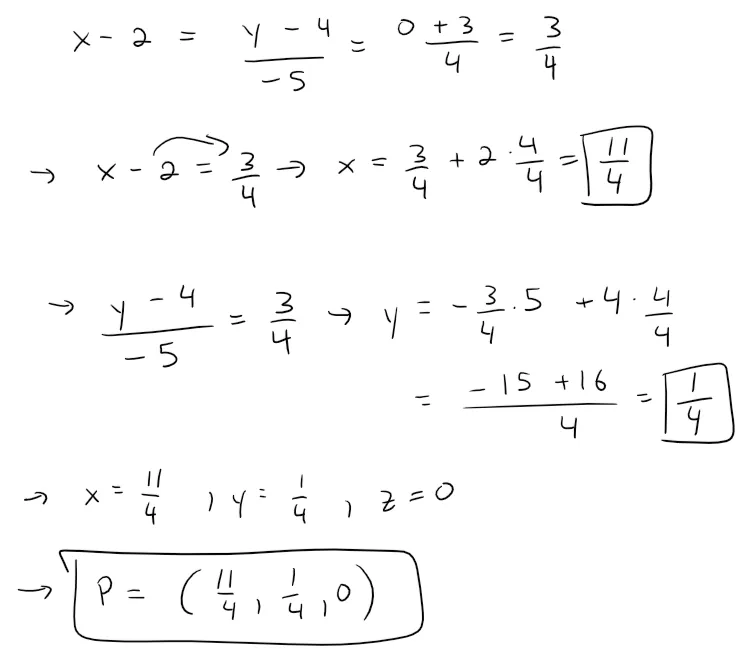
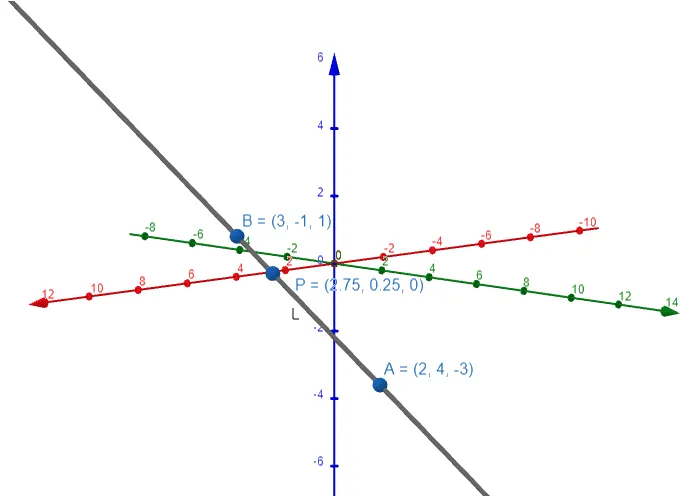
Thus the line intersects the xy-plane at the point P = (11/4, 1/4, 0).
Let's double check the graph using the GeoGebra 3D graphing calculator:

Note on Example 2
In general, the procedure of Example 2 shows that direction numbers of the line L through the points P0(x0, y0, z0) and P1(x1, y1, z1) are x1 - x0, y1 - y0, and z1 - z0 and so symmetric equations of L are:
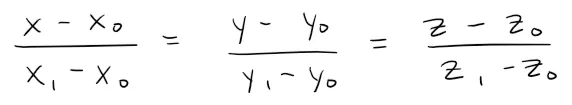
Equation of a Line Segment
Often, we need a description, not of an entire line, but of just a line segment.
How, for instance, could we describe the line segment AB in Example 2?
If we put t = 0 in the parametric equations in Example 2(a), we get the point A = (2, 4, -3).
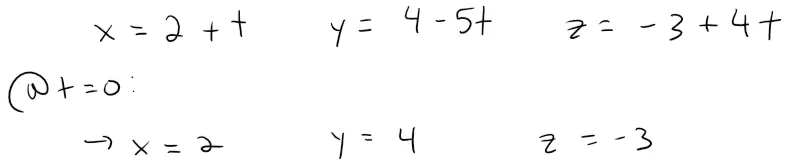
And if we put t = 1, we get the point B = (3, -1, 1).
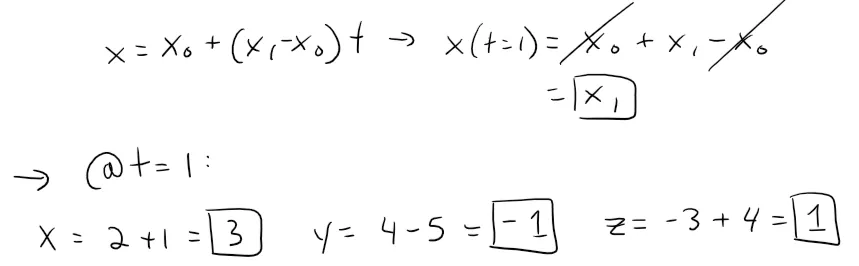
So the line segment AB is described by the vector equation:
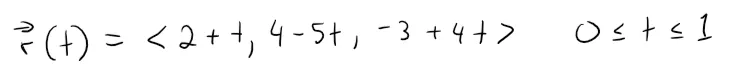
In general, we know from the earlier vector equation through the (tip of the) vector r0 in the direction of a vector v is r = r0 + tv.
If the line also passes through (the tip of) r1, then we can take v = r1 - r0 and so its vector equation is:
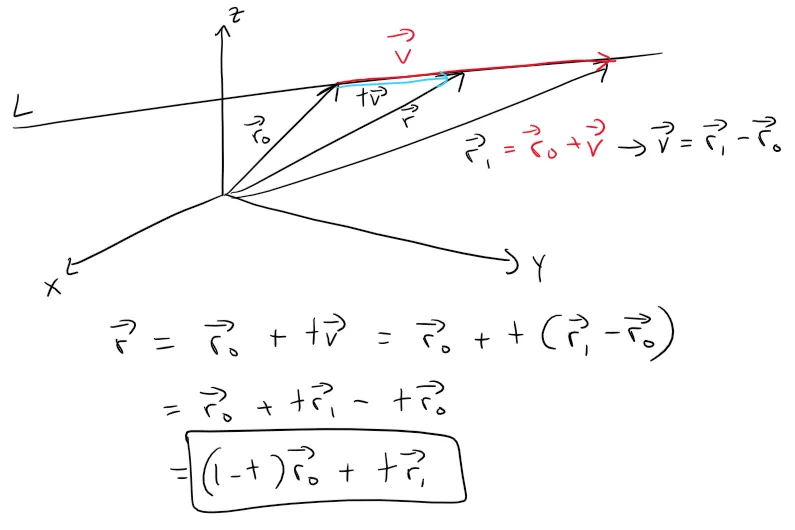
The line segment from r0 to r1 is given by the parameter 0 ≤ t ≤ 1.
Thus we can summarize as follows:
The line segment from r0 to r1 is given by the vector equation:
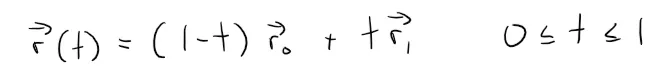
Notice that if we plug in t = 0 or t = 1, we get:
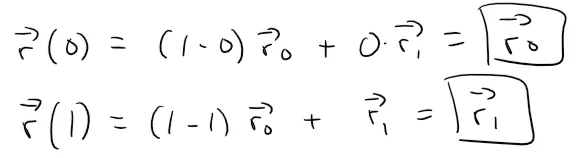
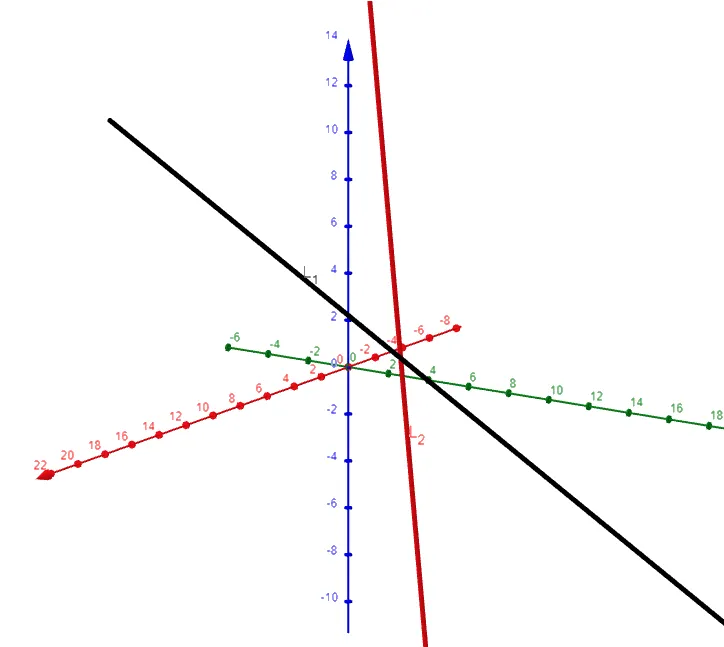
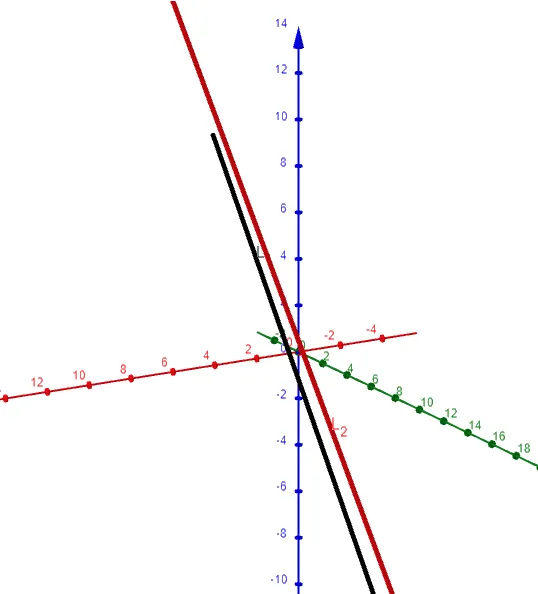
Example 3
Show that the lines L1 and L2 with parametric equations, shown below, are skew lines; that is, they do not intersect and are not parallel (and therefore do not lie in the same plane).
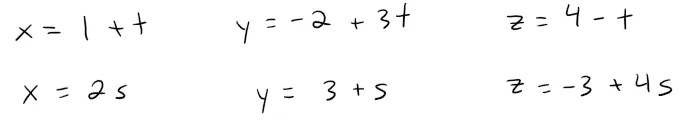
Solution:
The lines are not parallel because the corresponding direction vectors <1, 3, -1> and <2, 1, 4> are not parallel. (Their components are not proportional or scalar multiples of each other).
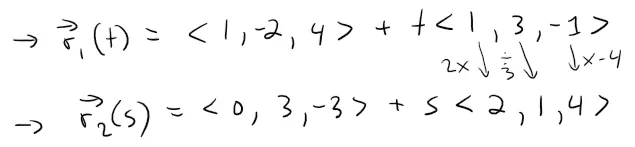
If L1 and L2 had a point of intersection, there would be values of t and s such that:
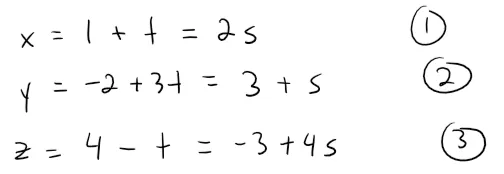
If we solve the first two equations, we get:
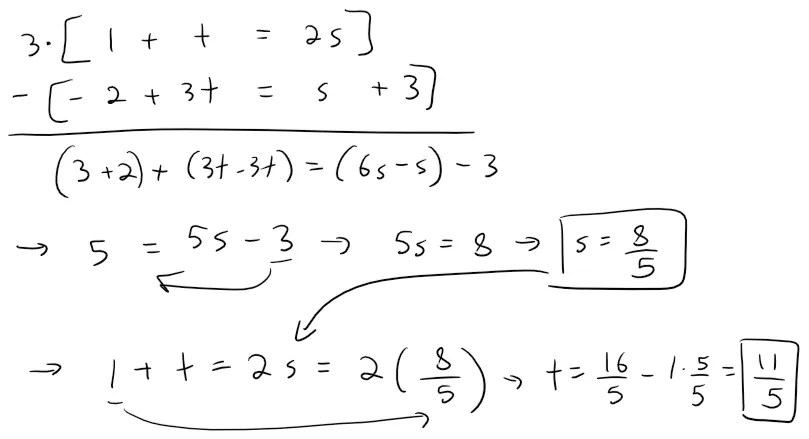
But if we plug these values into the third equation, we get:
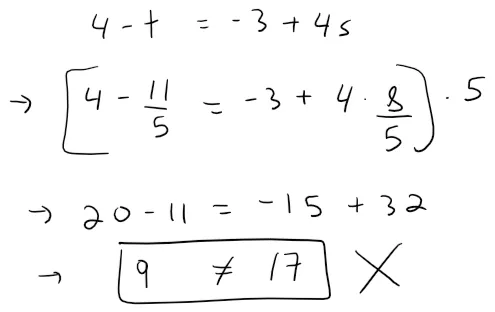
Therefore there are no values of t and s that satisfy the three equations, so L1 and L2 do not intersect.
Thus L1 and L1 are skew lines.
Here is a graph of the lines using the GeoGebra 3D graphing calculator:

Planes
Although a line in space is determined by a point and a direction, a plane in space is more difficult to describe.
Vector Equation of a Plane
A single vector parallel to a plane is not enough to convey the "direction" of the plane, but a vector perpendicular to the plane does completely specify its direction.
Thus a plane in space is determined by a point P0(x0, y0, z0) in the plane and a vector n that is orthogonal to the plane.
This orthogonal vector n is called a normal vector.
Let P(x, y, z) be an arbitrary point in the plane, and let r0 and r be the position vectors of P0 and P.
Then the vector r - r0 is represented by P0P as shown in the figure below.
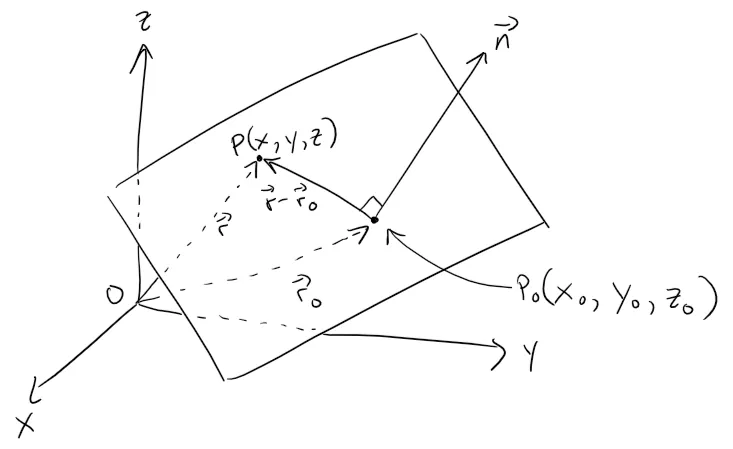
The normal vector n is orthogonal to every vector in the given plane.
In particular, n is orthogonal to r - r0, and using the fact that the dot product is zero for perpendicular vectors, so we have:
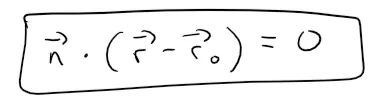
The above equation can be rewritten as:
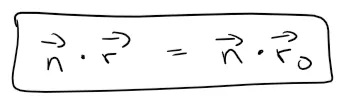
Either equation above is called a vector equation of the plane.
Scalar Equation of a Plane
To obtain a scalar equation for the plane, we write n = <a, b, c>, r = <x, y, z>, and r0 = <x0, y0, z0>.
Then the vector equation becomes:
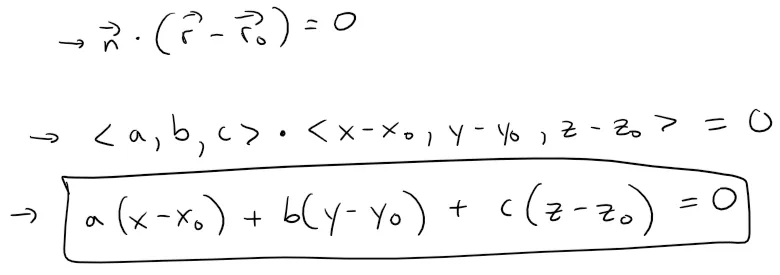
The above equation is called the scalar equation of the plane through P0(x0, y0, z0) with normal vector n = <a, b, c>.
Example 4
Find an equation of the plane through the point (2, 4, -1) with normal vector n = <2, 3, 4>.
Find the intercepts and sketch the plane.
Solution:
Putting in n = <a, b, c> = <2, 3, 4> and P0 = (x0, y0, z0) = (2, 4, -1) into the scalar equation of the plane, we obtain:
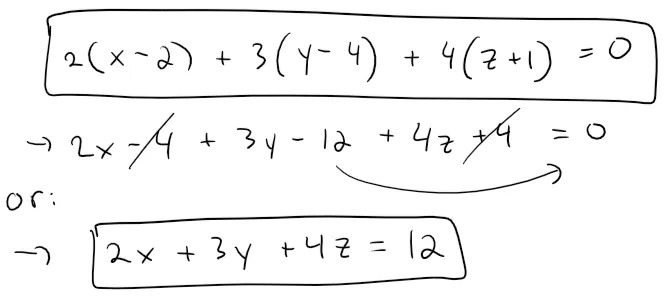
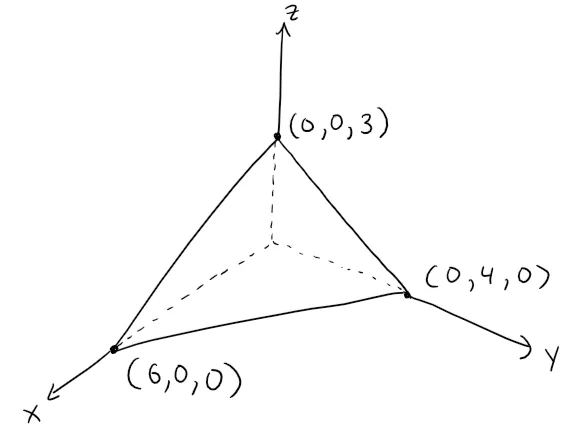
To find the x-intercept we set y = z = 0 in this equation and obtain x = 6.
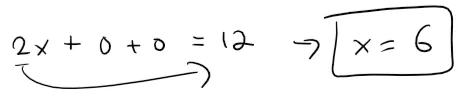
Similarly, the y-intercept is 4 and the z-intercept is 3.
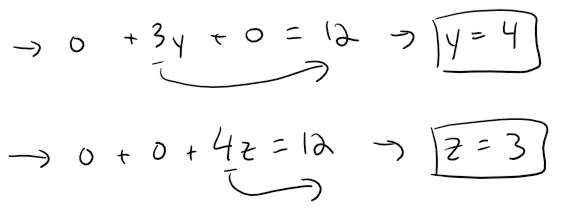
This enables us to sketch the portion of the plane that lies in the first octant.
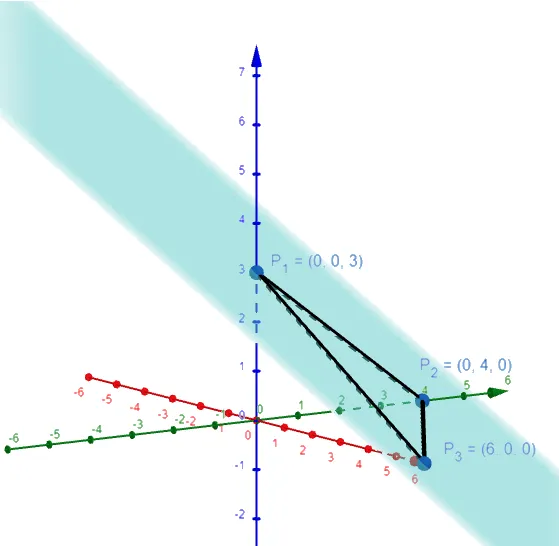
Let's graph this using the GeoGebra 3D graphing calculator:

Linear Equation of a Plane
By collecting terms in the scalar equation of the plane we can rewrite the equation of a plane as:
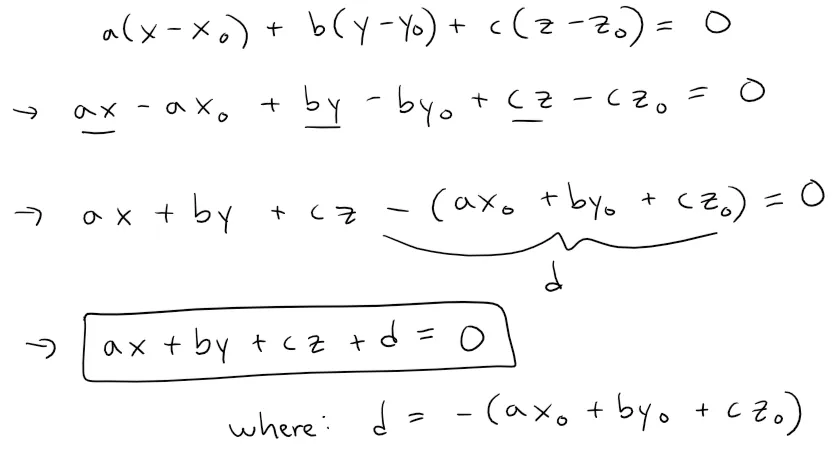
The above equation is called a linear equation in x, y, and z.
Conversely, it can be shown that if a, b, and c are not all 0, then the linear equation represents a plane with normal vector <a, b, c> (see Exercise 1 at the end of the video).
Example 5
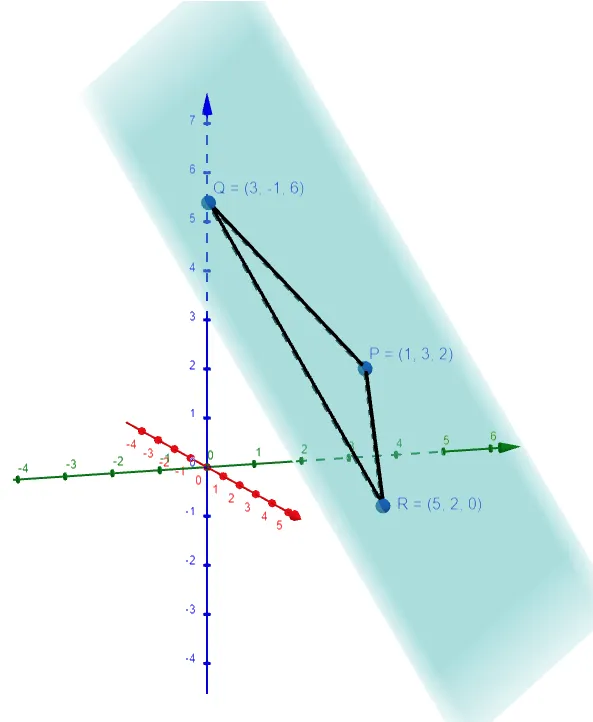
Find an equation of the plane that passes through the points P(1, 3, 2), Q(3, -1, 6), and R(5, 2, 0).
Solution:
The vectors a and b corresponding to PQ and PR are:
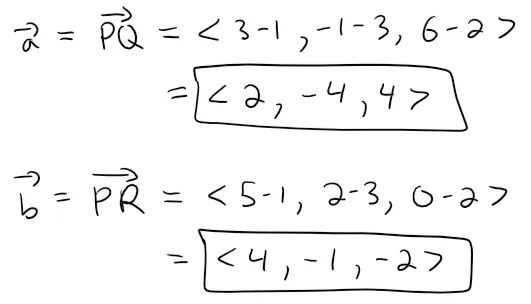
Since both a and b lie in the plane, their cross product a x b is orthogonal to the plane and can be taken as the normal vector, thus:
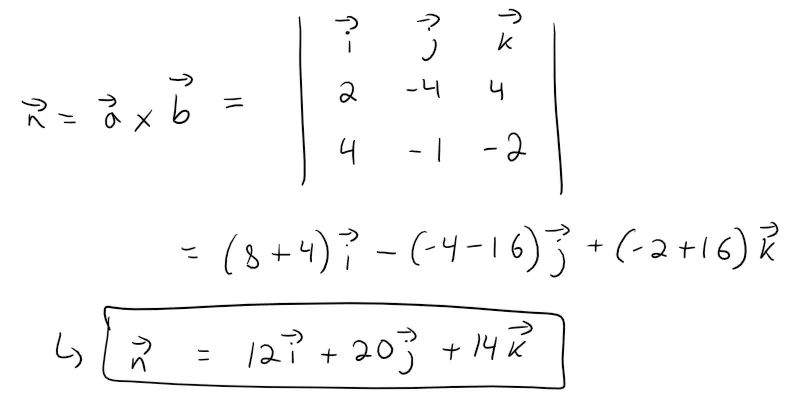
With the point P(1, 3, 2) and the normal vector n, an equation of the plane is:
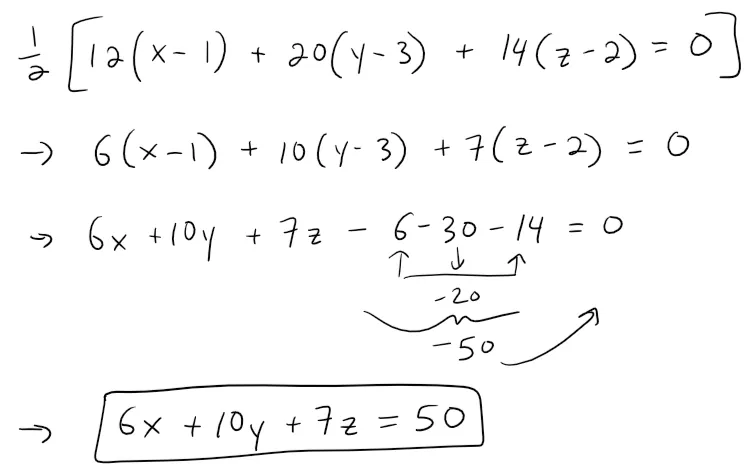
Let's graph this plane using the GeoGebra 3D graphing calculator:

Example 6
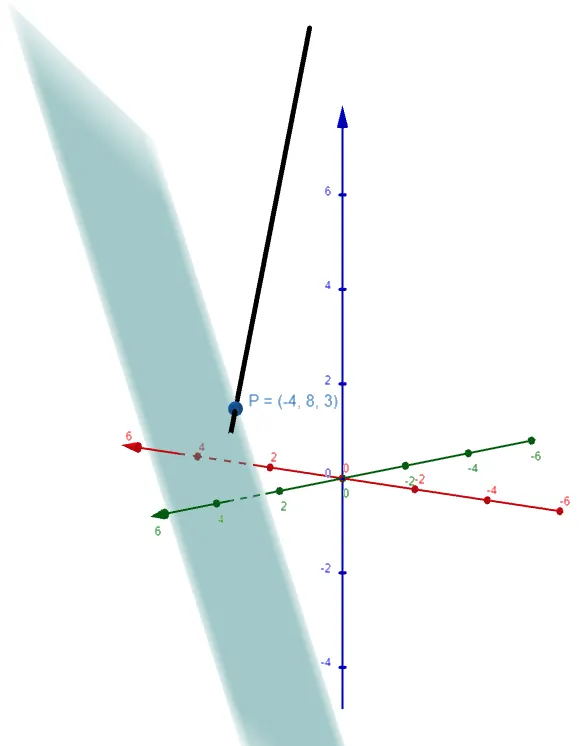
Find the point at which the line with parametric equations x = 2 + 3t, y = -4t, z = 5 + t intersects the plane 4x + 5y - 2z = 18.
Solution:
We substitute the expression for x, y, and z from the parametric equations into the equation of the plane:
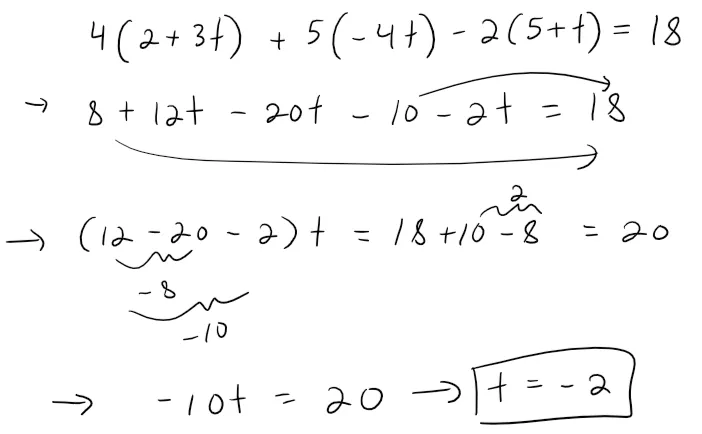
Therefor the point of intersection occurs when the parameter value is t = -2.
Plugging this value into the parametric equations of a line we get the point of intersection to be (-4, 8, 3).
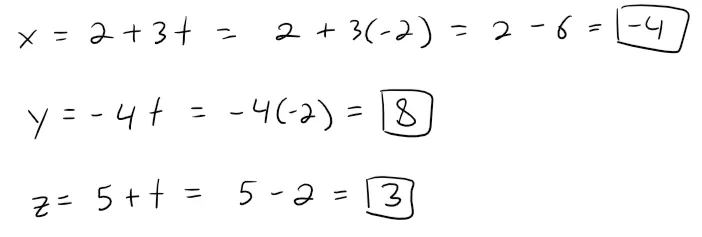
Let's graph this using the GeoGebra 3D graphing calculator:

Parallel Planes
Two planes are parallel if their normal vectors are parallel.
For instance, the planes x + 2y - 3z = 4 and 2x + 4y - 6z = 3 are parallel because their normal vectors n1 = <1, 2, -3> and n2 = <2, 4, -6> and n2 = 2n1.
If two planes are not parallel, then they intersect in a straight line and the angle between the two planes is defined as the acute angle between their normal vectors, as shown in the figure below.
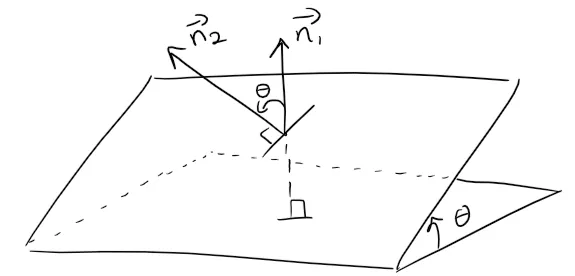
Example 7
(a) Find the angle between the planes: x + y + z = 1 and x - 2y + 3z = 1.
(b) Find symmetric equations for the line of intersection L of these two planes.
Solution to 7(a)
The normal vectors of these planes are:
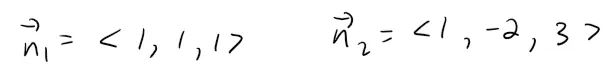
And so, if θ is the angle between the planes, we can apply the equation for the geometric interpretation of the dot product and get:
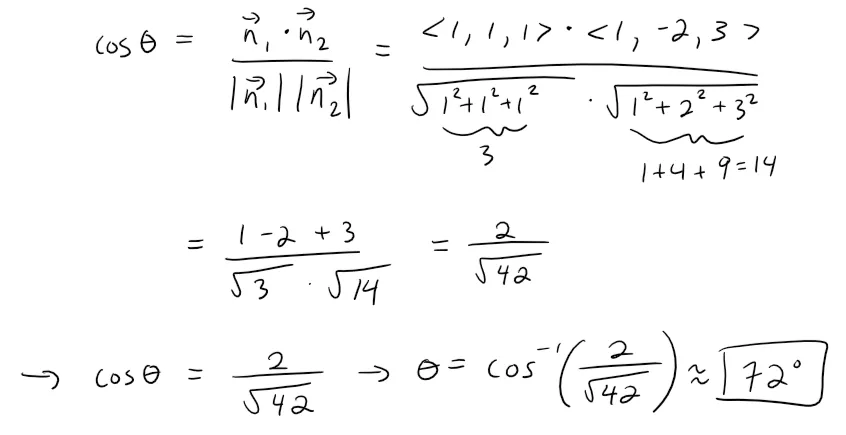
Calculation Check:
acos(2/sqrt(42)) = 72.02471619019111
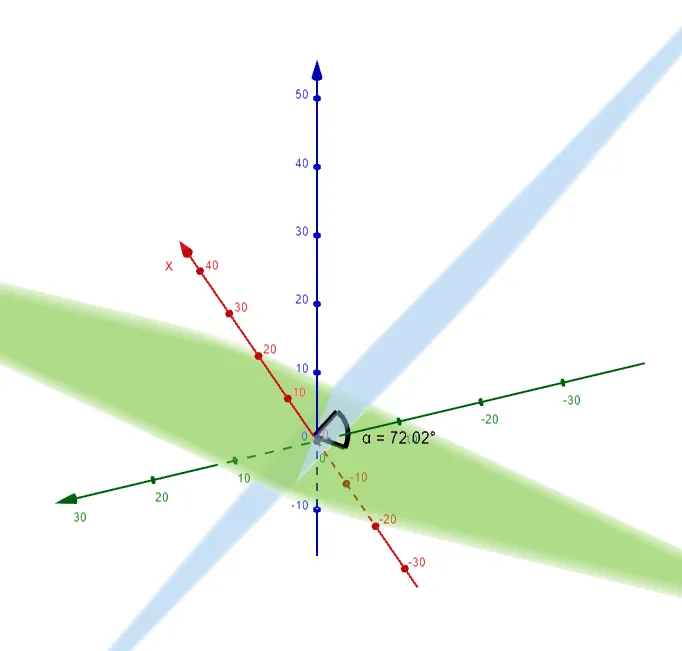
Let's graph out the planes and double check our work using the GeoGebra 3D graphing calculator:

Solution to 7(b)
We first need to find a point on L.
For instance, we can find the point where the line intersects the xy-plane by setting z = 0 in the equations of both planes.
This gives the equations x + y = 1 and x - 2y = 1, whose solution is x = 1, y = 0.
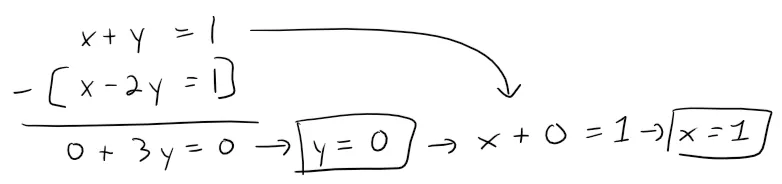
So the point (1, 0, 0) lies on L, since this point satisfies the equations of both planes.
Now we observe that, since L lies in both planes, it is perpendicular to both of the normal vectors.
Thus a vector v parallel to L is given by the cross product, since the cross product gives a perpendicular vector:
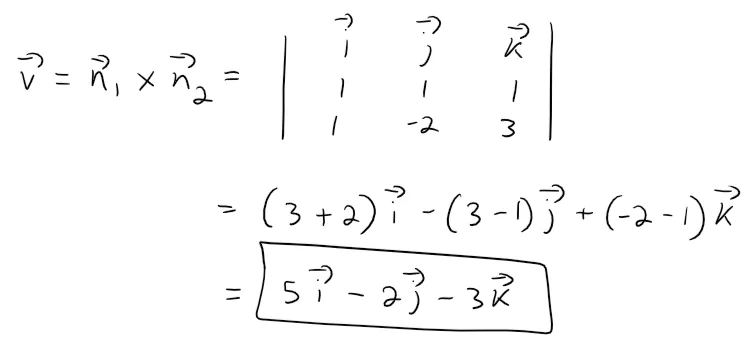
And so the symmetric equations of L can be written as:
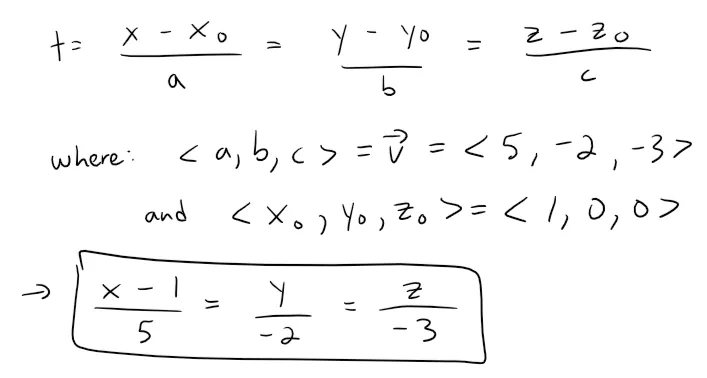
Let's graph out the line of intersection using the GeoGebra 3D graphing calculator:

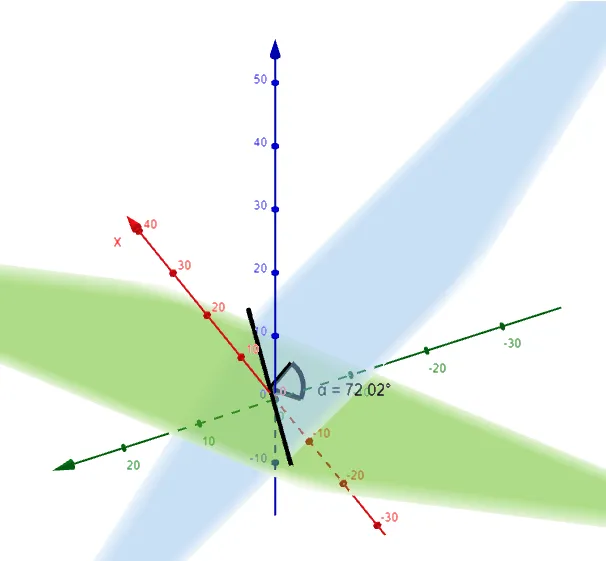
Note 1: Two Linear Equations Can Represent a Line
Since a linear equation in x, y, and z represents a plane and two nonparallel planes intersect in a line, it follows that two linear equations can represent a line.
The points (x, y, z) that satisfy both a1x + b1y + c1z + d1 = 0 and a2x + b2y + c2z + d2 = 0 lie on both of these planes, and so the pair of linear equations represents the line of intersection of the planes (if they are not parallel).
For instance, in Example 7 the line L was given as the line of intersection of the planes x + y + z = 1 and x - 2y + 3z = 1.
The symmetric equations that we found for L could be written as:
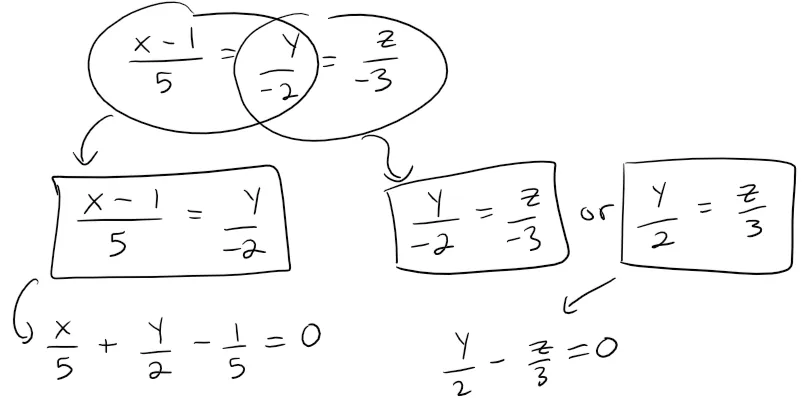
These equations again are a pair of linear equations.
They exhibit L as the line of the intersection of the planes (x - 1)/5 = y/(-2) and y/2 = z/3 as in the figure below.
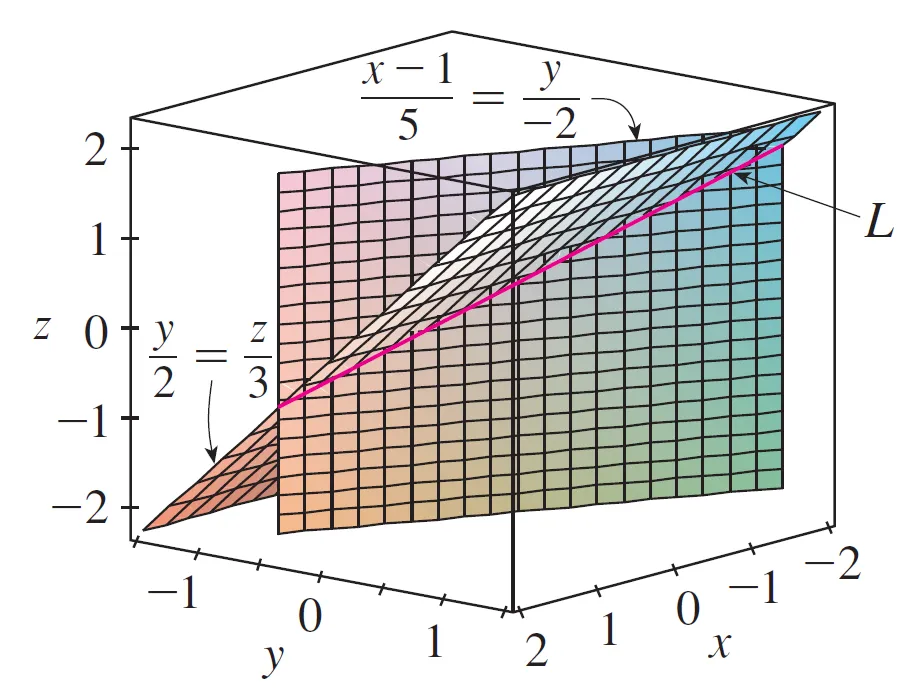
The above figure shows that the line L in Example 7 can also be regarded as the line of intersection of planes from its symmetric equations.
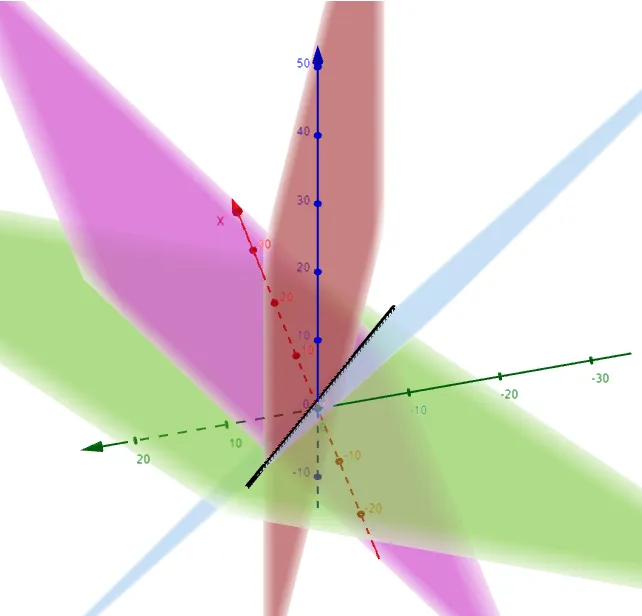
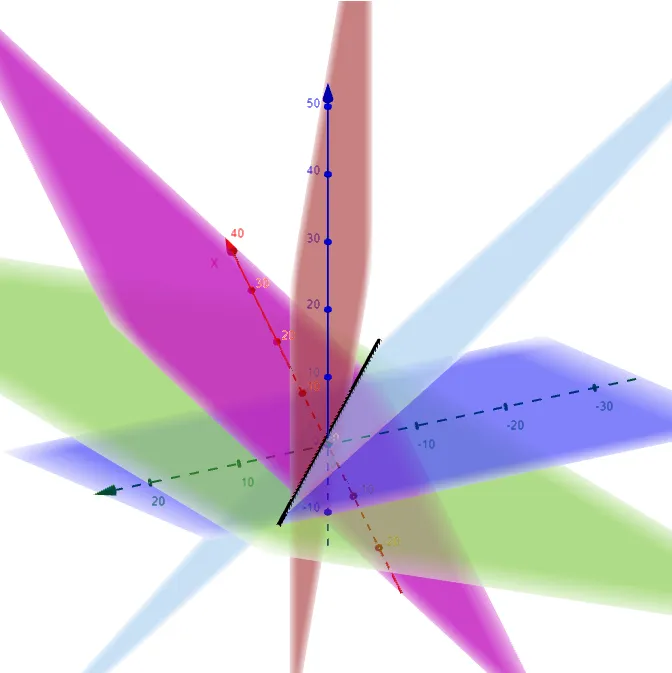
We can graph out the 4 equations of the planes (two from Example 7 and two from the symmetric equations) and show that they all intersect at the same common line! #Amazing

In general, when we write the equations of a line in symmetric form:
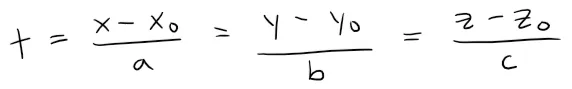
Then we can regard the line as the line of intersection of the two planes:
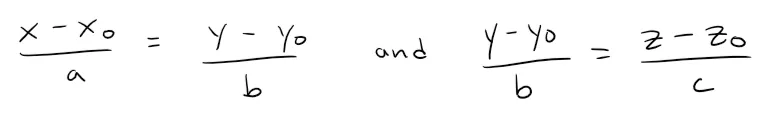
Note 2: Line of Intersection from Two Parametric Planes
Note that another way to find the line of intersection is to solve the equation of the planes for two of the variables in terms of the third, which can be taken as the parameter.
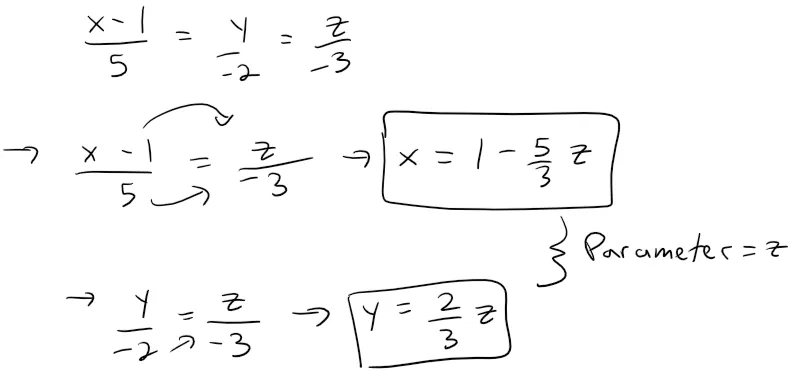

Example 8: Distance from a Point to a Plane
Find a formula for the distance D from a point P1(x1, y1, z1) to the plane ax + by + cz + d = 0.
Solution:
Let P0(x0, y0, z0) be any point in the given plane and let b be the vector corresponding to P0P1, then:
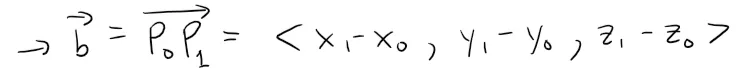
From the figure below you can see that the distance D from P1 to the plane is equal to the absolute value of the scalar projection of b onto the normal vector n = <a, b, c>.
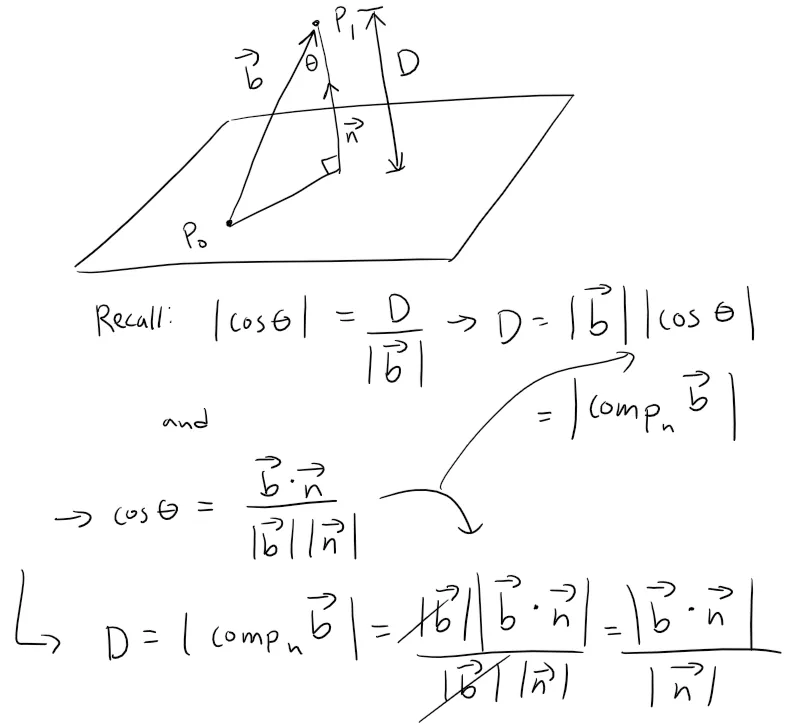
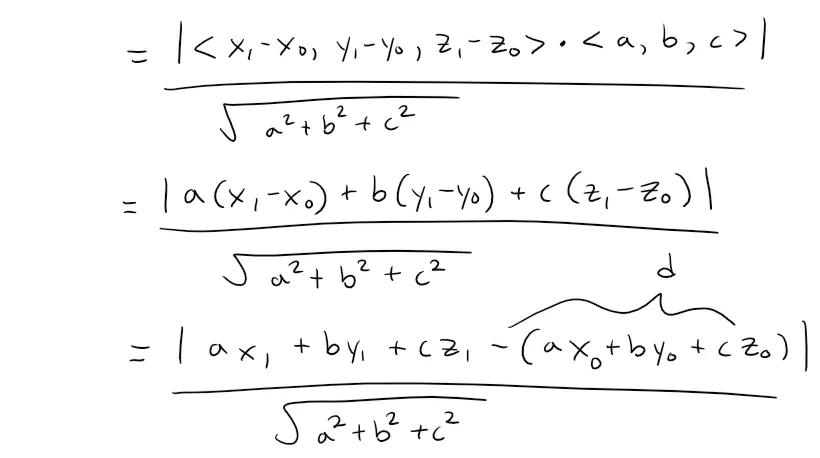
Since P0 lies in the plane, its coordinates satisfy the equation of the plane and so we have ax0 + by0 + cz0 + d = 0.
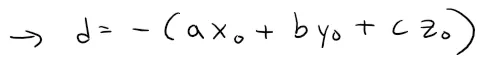
Thus the formula for D can be written as:
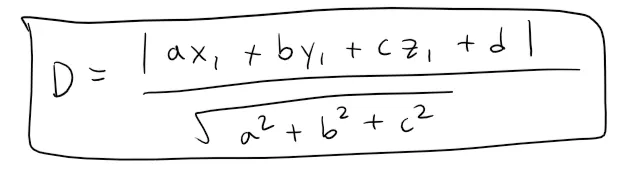
Example 9
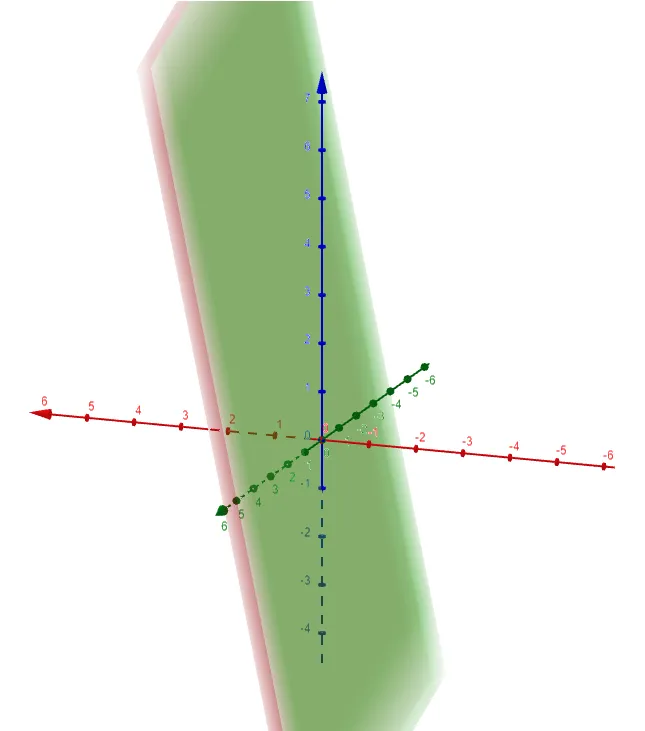
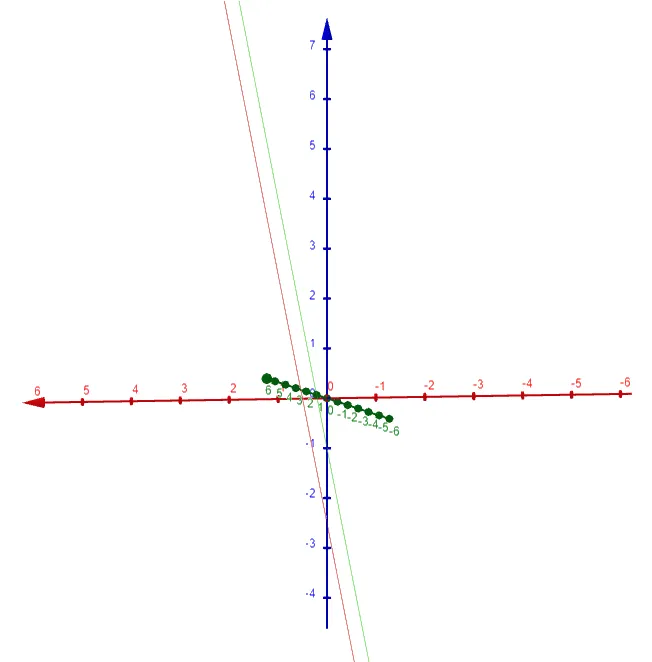
Find the distance between the parallel planes 10x + 2y - 2z = 5 and 5x + y - z = 1.
Solution:
First we note that the planes are parallel because their normal vectors <10, 2, -2> and <5, 1, -1> are parallel, that is they are multiples of each other.
To find the distance D between the planes, we choose any point on one plane and calculate its distance to the other plane.
In particular, if we put y = z = 0 in the equation of the first plane, we get 10x = 5 and so (1/2, 0, 0) is a point in this plane.
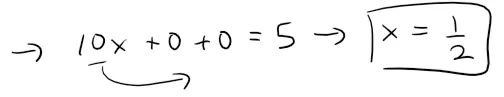
Thus by the distance formula the distance between (1/2, 0, 0) and the plane 5x + y - z - 1 = 0 is:
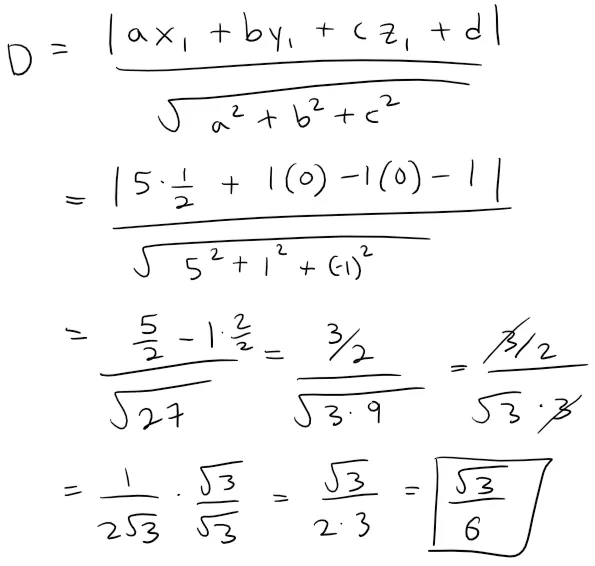
So the distance between the planes is √(3/6) = sqrt(3)/6 = 0.288675134594813.
Let's graph the two planes and calculate its distance using the amazing GeoGebra 3D graphing calculator:
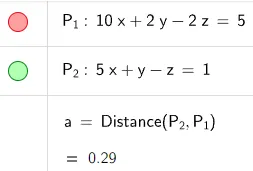
Example 10
In Example 3 we showed that the following lines are skew:
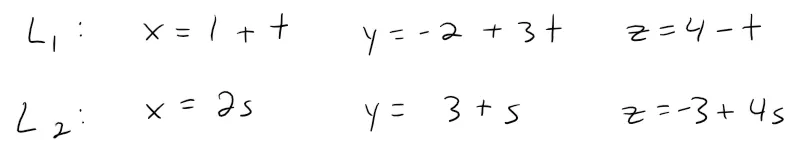
Find the distance between them.
Solution:
Since the two lines L1 and L2 are skew, they can be viewed as lying on two parallel planes P1 and P2.
The distance between L1 and L2 is the same as the distance between P1 and P2, which can be computed as in Example 9.
The common normal vector to both planes must be orthogonal to both v1 = <1, 3, -1> (the direction of L1) and v2 = <2, 1, 4> (the direction of L2).
So a normal vector is:
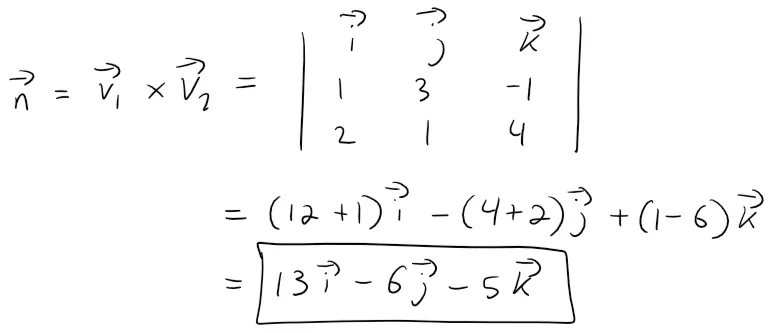
If we put s = 0 in the equations of L2, we get the point (0, 3, -3) on L2 and so an equation for P2 is:
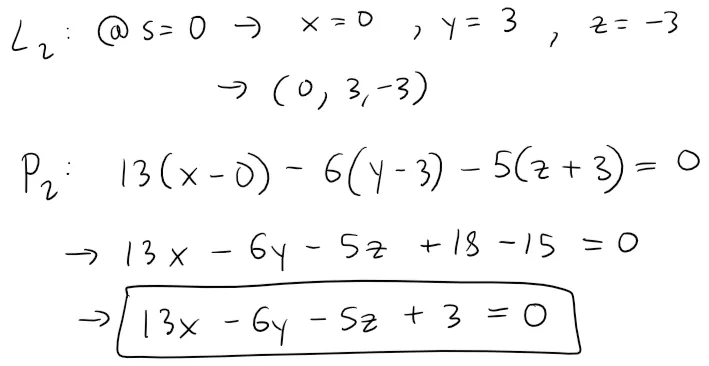
If we now set t = 0 in the equations for L1, we get the point (1, -2, 4) on P1.
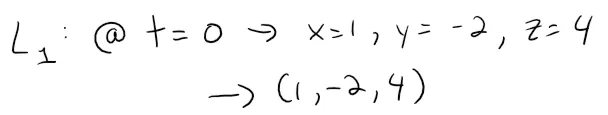
So the distance between L1 and L2 is the same as the distance from (1, -2, 4) to 13x -6y - 5z + 3 = 0.
Thus by the distance formula, the distance is:
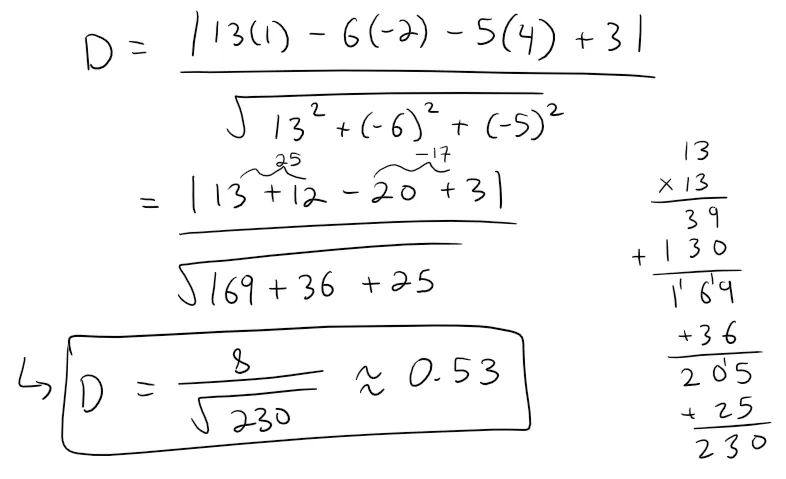
Calculation Check:
13 - 6·(-2) - 5·(4) + 3 = 8
13^2 + 6^2 + 5^2 = 230
8/sqrt(230) = 0.52750437871663
Let's graph and double check our calculations using the GeoGebra 3D graphing calculator:

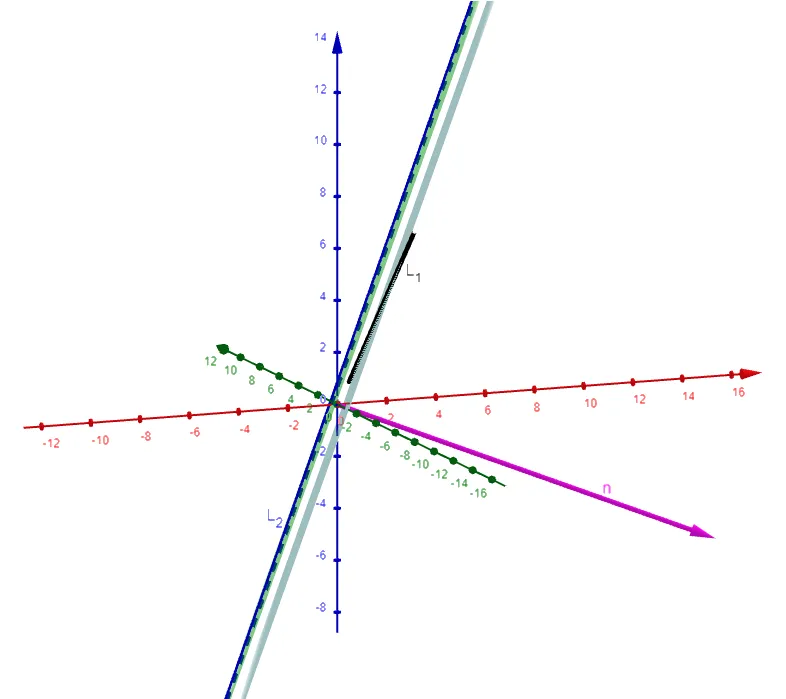
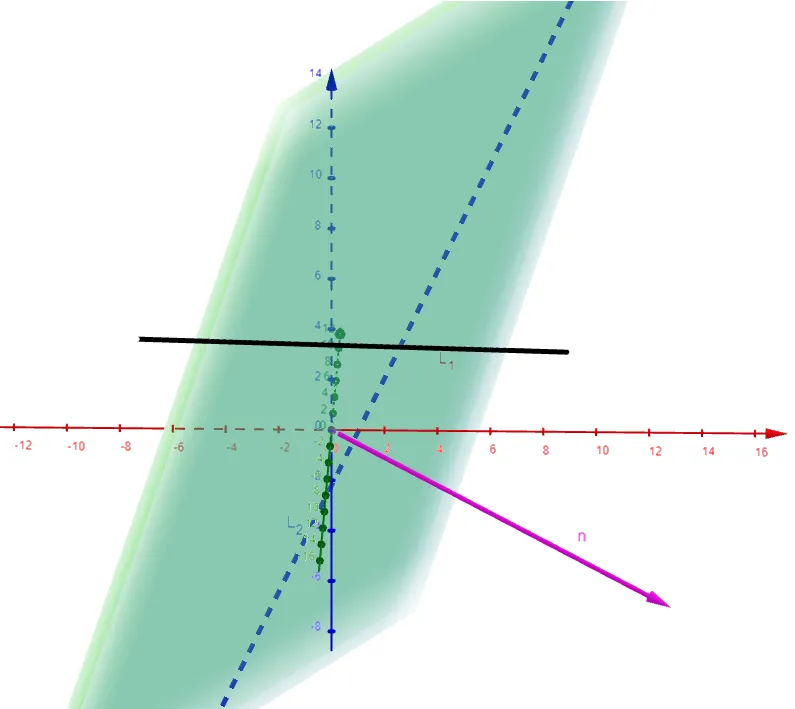

Note that in GeoGebra the distance formula required that I know the equation of both planes, and in which I solved the first plane as follows:
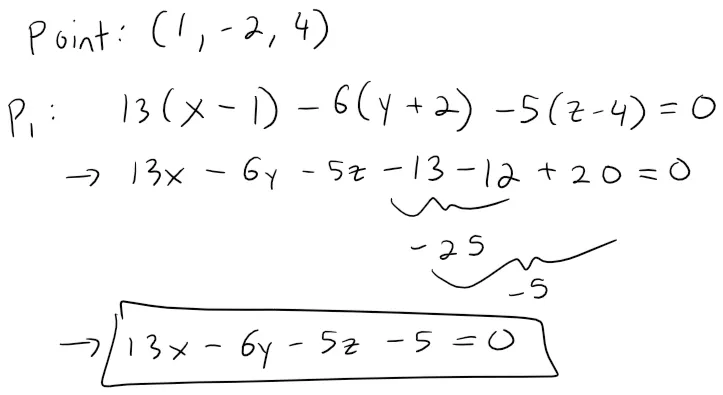
Exercise 1
If a, b, and c are not all 0, show that the equation ax + by + cz + d = 0 represents a plane and <a, b, c> is a normal vector to the plane.
Hint: Suppose a ≠ 0 and rewrite the equation in the form:
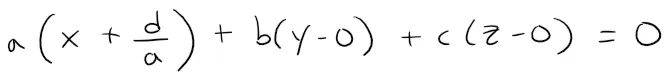
Solution:
Since a, b, and c are not all 0, then we can assume that one of them is not 0.
If a ≠ 0, then we can write the equation as:
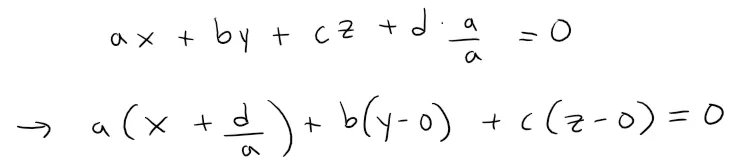
We can rewrite this as a dot product.
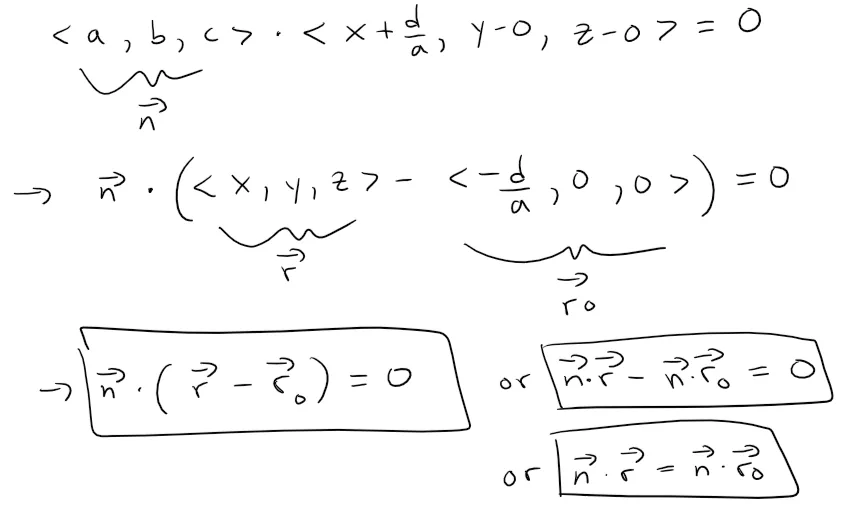
Thus we have shown that the given equation can be written as a vector equation of a plane with normal vector n = <a, b, c> and r - r0 representing a vector on the plane.