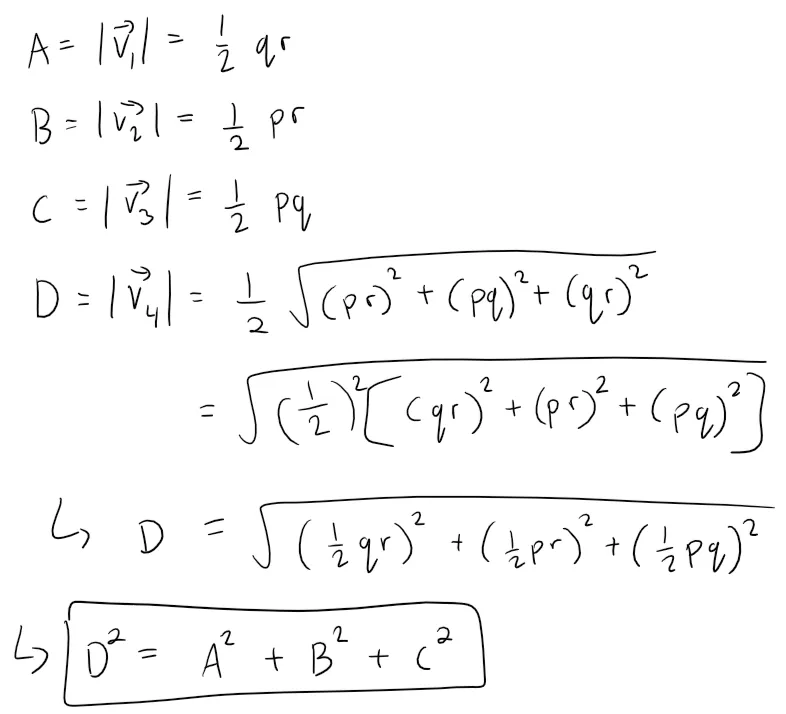In this video I go over the Discovery Project titled The Geometry of a Tetrahedron. Discovery Projects are advanced math problems in each chapter of my calculus book, and this one is part of the Vectors and Geometry of Space chapter. This project involves 3 Questions regarding the tetrahedron, which is a triangular pyramid. The first question involves finding the areas of each triangular face using the Cross Product. The second question involves finding the volume of a tetrahedron when written in coordinate vector form. And the third question involves deriving the 3D version of the Pythagorean Theorem, which is: the 3 triangular areas squared at a vertex sum up to equal the square of the opposite triangular area!

The topics covered as well as their timestamps are listed below.

• Introduction: 0:00
• Calculus Book Reference: 0:56
• Sections in Calculus Book Chapter: 1:12
• Topics to Cover: 2:03

1. Discovery Project: The Geometry of a Tetrahedron: 2:25
2. 3 Questions: 3:05
   • Question 1: 5:00
   • Question 2: 34:59
     • Solution to Part (a): 36:10
       • The Equation of a Plane: 41:20
       • The Distance from a Point to a Plane: 45:31
     • Solution to Part (b): 52:43
   • Question 3: 1:05:35

Download video notes: https://1drv.ms/b/s!As32ynv0LoaIicNsAiLSiBI1ivS39w?e=V33CkF

View video sections playlist: https://www.youtube.com/playlist?list=PLai3U8-WIK0GoEi9wxl8nTFcfw1ay-_1T

View the full Vectors and the Geometry of Space series: https://www.youtube.com/playlist?list=PLai3U8-WIK0FjJpwnxwdrOR7L8Ul8VZoZ

---

Watch video on:

• 3Speak:
• Odysee: https://odysee.com/@mes:8/Discovery-Project-Geometry-of-a-Tetrahedron:2
• BitChute:
• Rumble: https://rumble.com/v2cja8i-discovery-project-the-geometry-of-a-tetrahedron.html
• DTube:
• YouTube:

---

View Video Notes Below!

---

Download these notes: Link is in video description.
View these notes as an article: @mes
Subscribe via email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donate
Buy MES merchandise! https://mes.fm/store
More links: https://linktr.ee/matheasy
Follow my research in real-time on my MES Links Telegram: https://t.me/meslinks
Subscribe to MES Truth: https://mes.fm/truth

Reuse of my videos:

• Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.

Fight back against censorship:

• Bookmark sites/channels/accounts and check periodically
• Remember to always archive website pages in case they get deleted/changed.

Recommended Books:

• "Where Did the Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook

Join my forums!

• Hive community: created/hive-128780
• Reddit: https://reddit.com/r/AMAZINGMathStuff
• Discord: https://mes.fm/chatroom

Follow along my epic video series:

• #MESScience: https://mes.fm/science-playlist
• #MESExperiments: @mes/list
• #AntiGravity: @mes/series
  -- See Part 6 for my Self Appointed PhD and #MESDuality breakthrough concept!
• #FreeEnergy: https://mes.fm/freeenergy-playlist
• #PG (YouTube-deleted series): @mes/videos

---

NOTE #1: If you don't have time to watch this whole video:

• Skip to the end for Summary and Conclusions (if available)
• Play this video at a faster speed.
  -- TOP SECRET LIFE HACK: Your brain gets used to faster speed!
  -- MES tutorial: @mes/play-videos-at-faster-or-slower-speeds-on-any-website
• Download and read video notes.
• Read notes on the Hive blockchain #Hive
• Watch the video in parts.
  -- Timestamps of all parts are in the description.

Browser extension recommendations:

• Increase video speed: https://mes.fm/videospeed-extension
• Increase video audio: https://mes.fm/volume-extension
• Text to speech: https://mes.fm/speech-extension
  --Android app: https://mes.fm/speech-android

---

Vectors and the Geometry of Space: The Cross Product

Calculus Book Reference

Note that I mainly follow along the following calculus book:

• Calculus: Early Transcendentals 7th Edition by James Stewart
• Note: In the earlier videos I used the 6th edition.

---

Sections in Calculus Book Chapter

I have made a list of the sections in this particular chapter with links to the Hive post of the videos I have already finished.

Vectors and the Geometry of Space

1. 3-D Coordinate Systems
2. Vectors
   • Complex Numbers as Rotation Matrices
     • Playlist
3. The Dot Product
   • Playlist
4. The Cross Product
   • Playlist
   • Discovery Project: The Geometry of a Tetrahedron (Current Video)
5. Equations of Lines and Planes
   • Laboratory Project: Putting 3D in Perspective
6. Cylinders and Quadric Surfaces
7. Review
   • True-False Quiz
8. Problems Plus

---

Topics to Cover

Note that the timestamps will be included in the video description for each topic listed below.

1. Discovery Project: The Geometry of a Tetrahedron
2. 3 Questions
   • Question 1
   • Question 2
     • Solution to Part (a)
       • The Equation of a Plane
       • The Distance from a Point to a Plane
     • Solution to Part (b)
   • Question 3

---

Discovery Project: The Geometry of a Tetrahedron

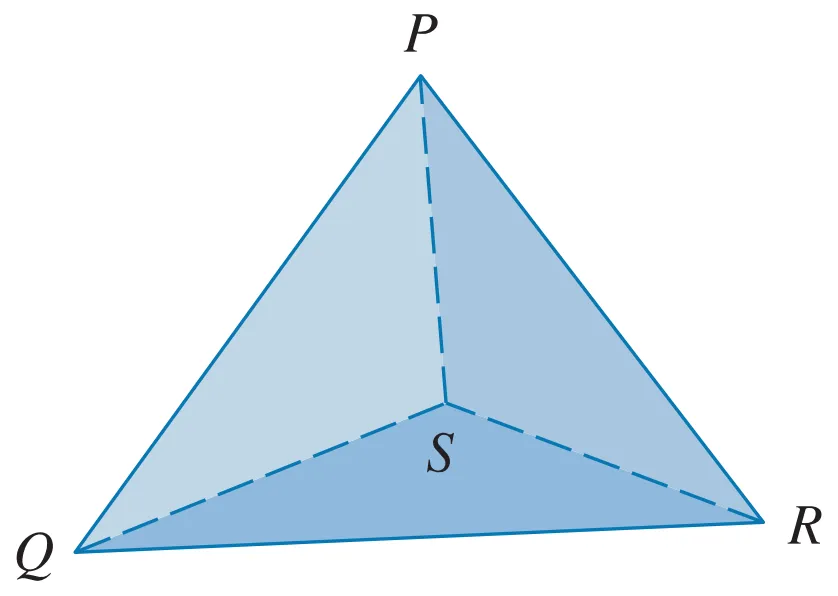
A tetrahedron is a solid with four vertices, P, Q, R, and S, and four triangular faces, as shown in the figure.

Question 1

Let v₁, v₂, v₃, and v₄ be vectors with lengths equal to the areas of the faces opposite the vertices P, Q, R, and S, respectively, and directions perpendicular to the respective faces and pointing outward.

Show that:

v₁ + v₂ + v₃ + v₄ = 0

Question 2

The volume V of a tetrahedron is one-third the distance from a vertex to the opposite face [MES Correction: This is actually the height of the tetrahedron] times the area of that face.

(a) Find a formula for the volume of a tetrahedron in terms of the coordinates of its vertices P, Q, R, and S.

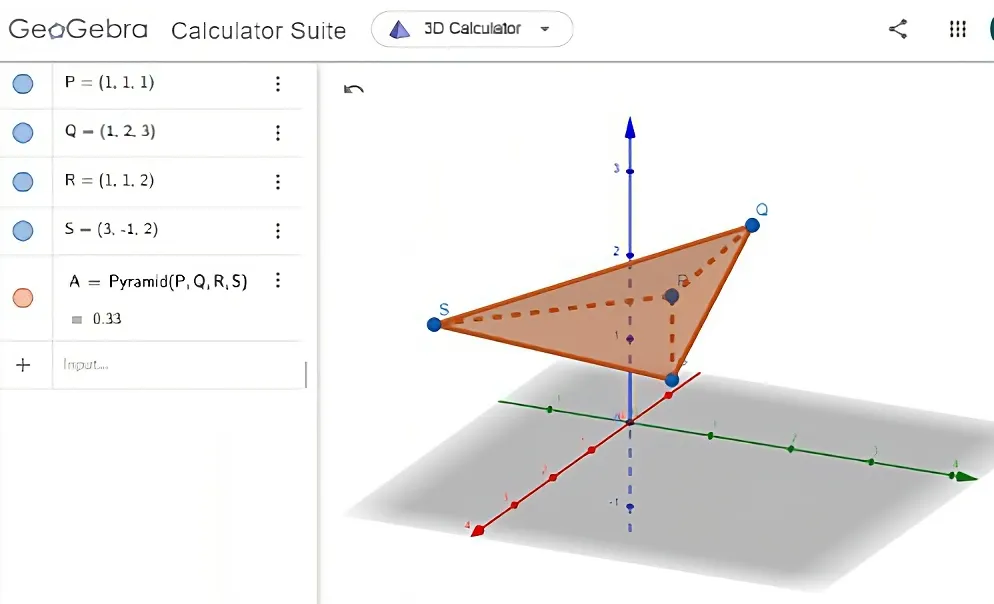
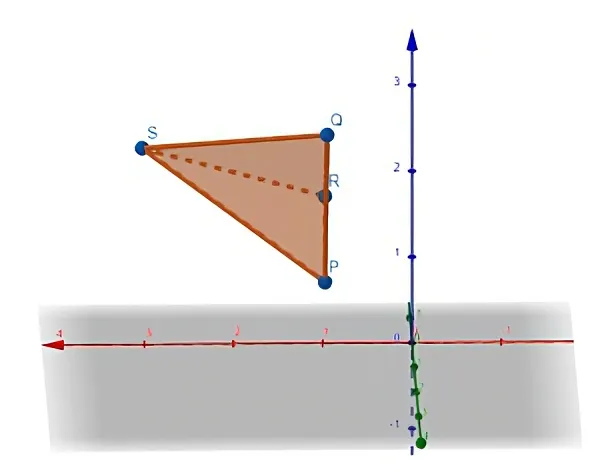
(b) Find the volume of a tetrahedron whose vertices are P(1, 1, 1), Q(1, 2, 3), R(1, 1, 2), and S(3, -1, 2).

Question 3

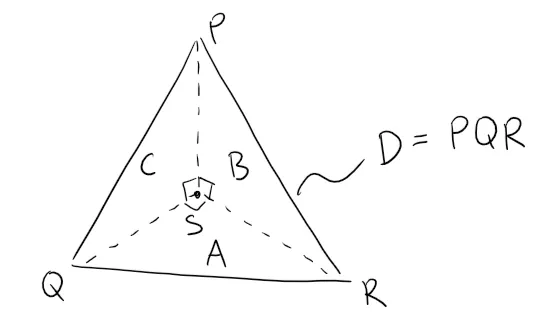
Suppose the tetrahedron in the figure has a trirectangular vertex S. (This means that the three angles at S are all right angles.)

Let A, B, and C be the areas of the three faces that meet at S, and let D be the area of the opposite face PQR.

Using the result of Question 1, or otherwise, show that:

D² = A² + B² + C²

(This is a three-dimensional version of the Pythagorean Theorem.)

---

Question 1

Let v₁, v₂, v₃, and v₄ be vectors with lengths equal to the areas of the faces opposite the vertices P, Q, R, and S, respectively, and directions perpendicular to the respective faces and pointing outward.

Show that:

v₁ + v₂ + v₃ + v₄ = 0

Solution:

Recall that the length of the cross product is equal to the area of a parallelogram formed by the two vectors, therefore half that is the area of a triangle.

Thus the lengths of the vectors v₁, v₂, v₃, and v₄ can be written as half the cross product of 2 sides of each triangle face.

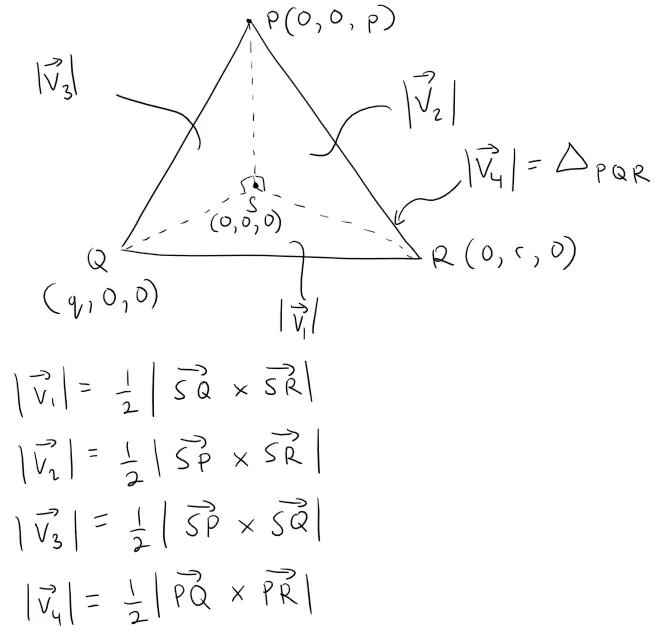
We can calculate each area by first writing the cross product in determinate form.

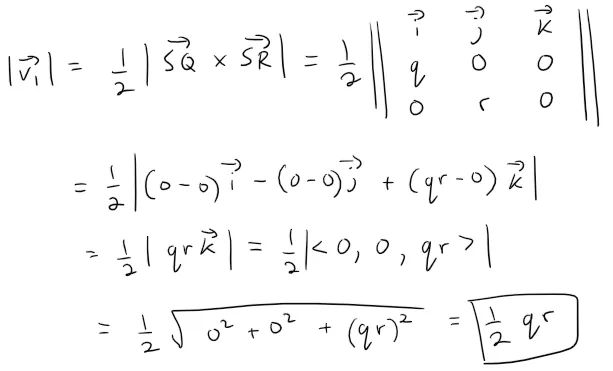
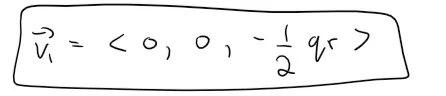
Since we are told that the direction of the vectors point outwards perpendicular from the faces, v₁ must be pointing downwards away from the tetrahedron.

Similarly for the remaining 3 vectors we have:

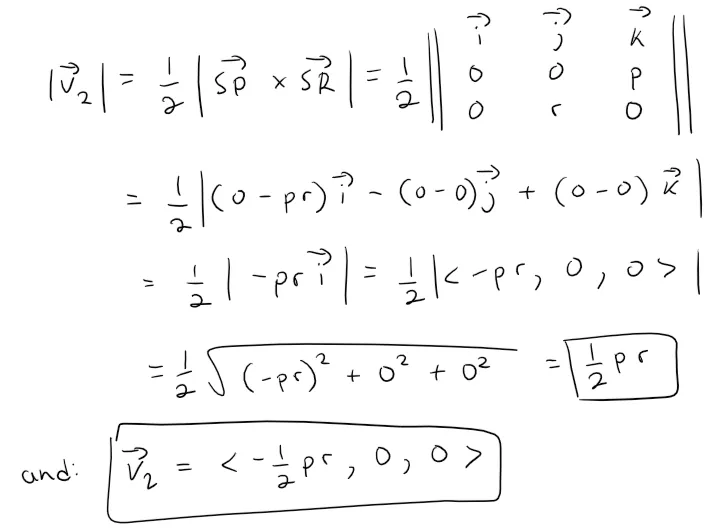
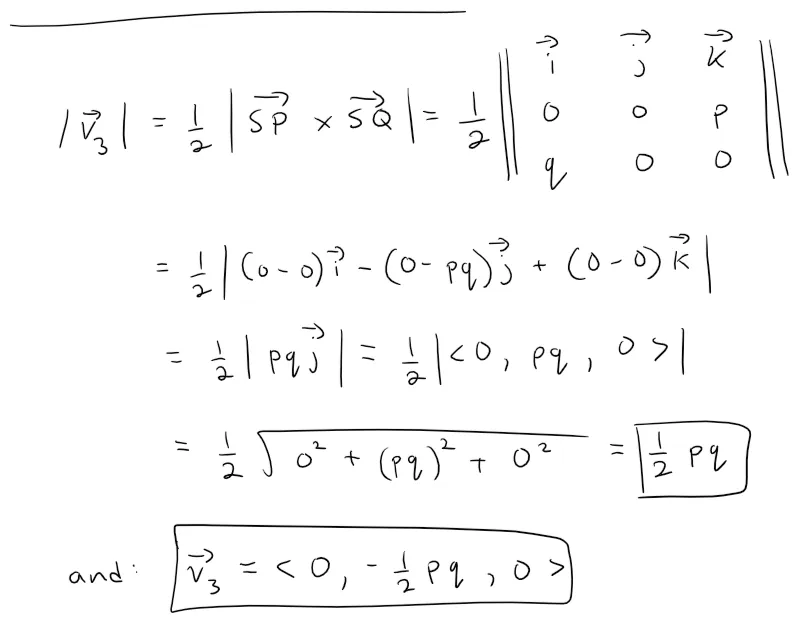
Note that for |v₄|, since it involves vectors not relative to the origin, we need to calculate the position vector, which is the equivalent vector but starting from the origin and is the difference in each coordinate component.

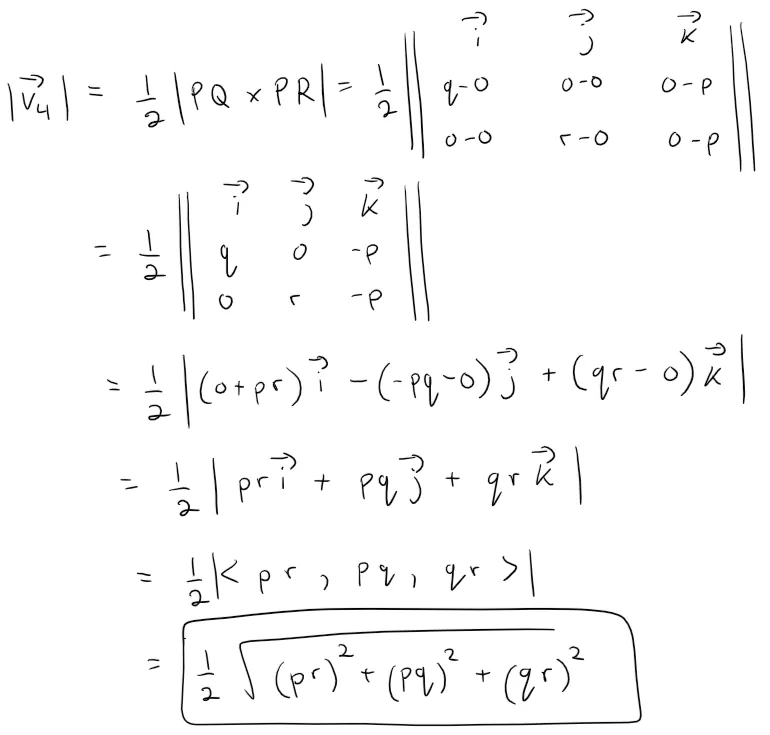
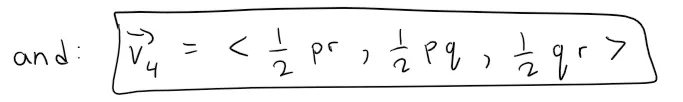
Note that the vector v₄ is pointing out of the page in the positive direction away from the PQR triangle.

Therefore, if we add all the vectors we get:

---

Question 2

The volume V of a tetrahedron is one-third the distance from a vertex to the opposite face [MES Correction: This is actually the height of the tetrahedron] times the area of that face.

I will look to provide a proof in a later video.

(a) Find a formula for the volume of a tetrahedron in terms of the coordinates of its vertices P, Q, R, and S.

(b) Find the volume of a tetrahedron whose vertices are P(1, 1, 1), Q(1, 2, 3), R(1, 1, 2), and S(3, -1, 2).

Solution to Part (a)

After finishing the filming of this video I realized that the formula for a tetrahedron as stated in Question 2 is actually wrong!

The actual formula involves the height of the tetrahedron, and not the distance from vertex to opposite face; this is evident for a skewed tetrahedron.

I think what the Discovery Project actually meant was the distance to the plane that contains the opposite triangle face, which is the same thing as stating the height of the tetrahedron.

Thus we can write the volume of a tetrahedron in coordinate form as follows:

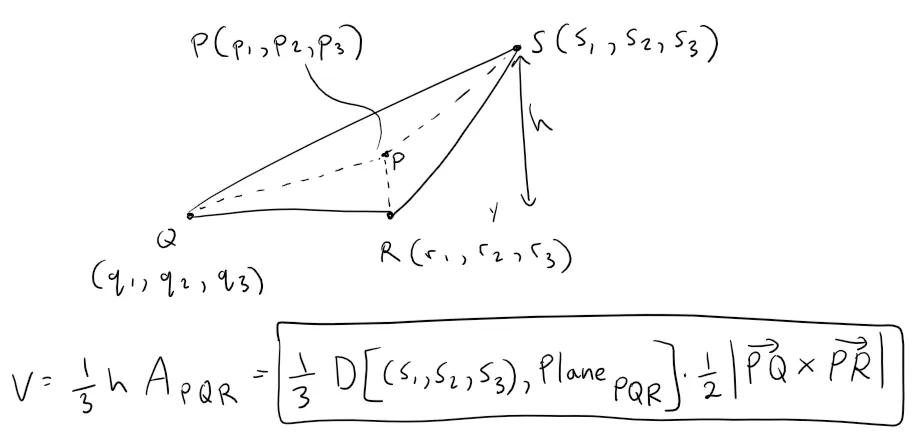
The Equation of a Plane

Note that the equation of a plane can be derived based on the fact that the dot product is equal to 0 for perpendicular vectors.

The Distance from a Point to a Plane

The equation for the distance from a point to a plane (which I will prove in a later video) is given by:

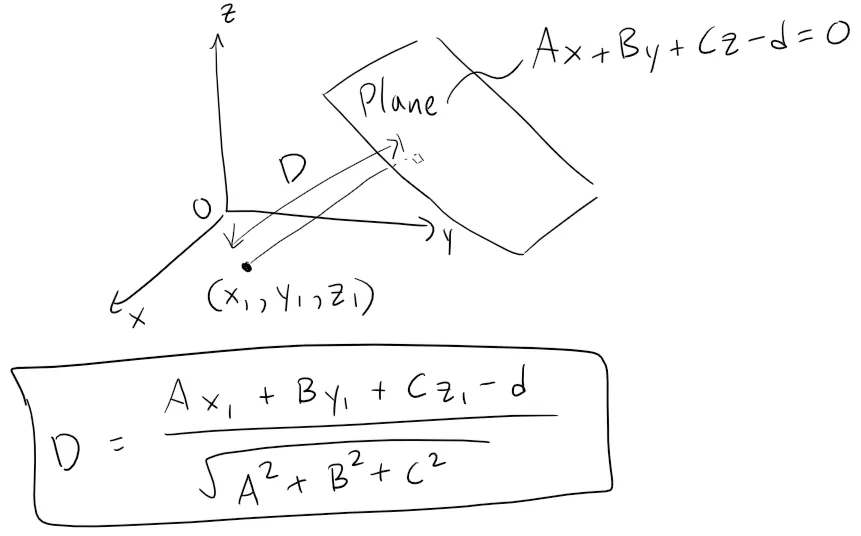
Thus putting this all together, the volume of a tetrahedron in coordinate form is:

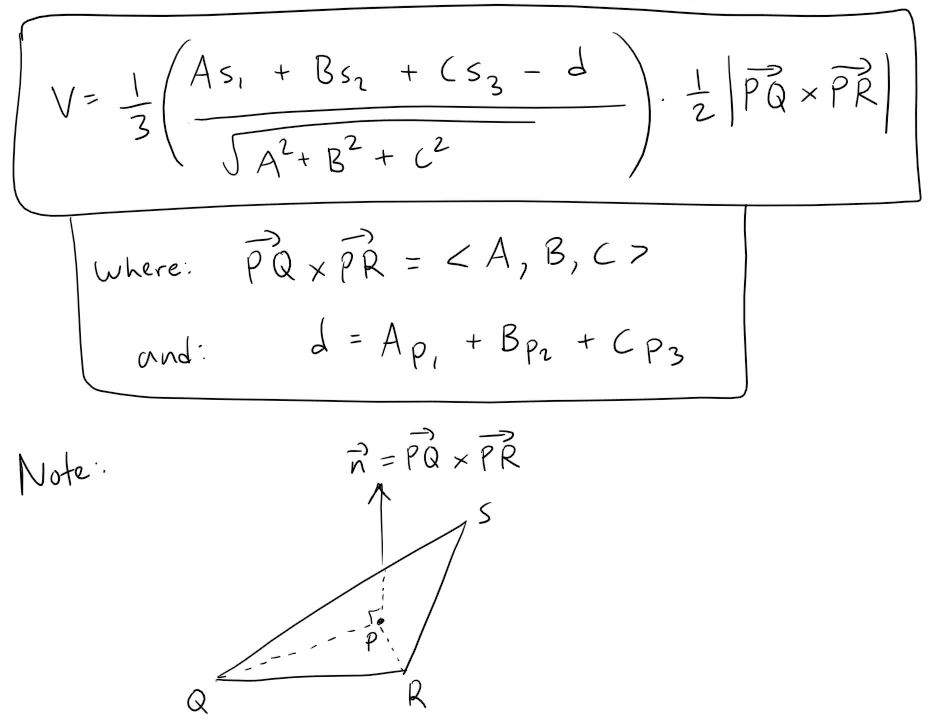
Solution to Part (b)

The first step is to derive the position vectors PQ and PR and then we can compute their cross product and cross product length.

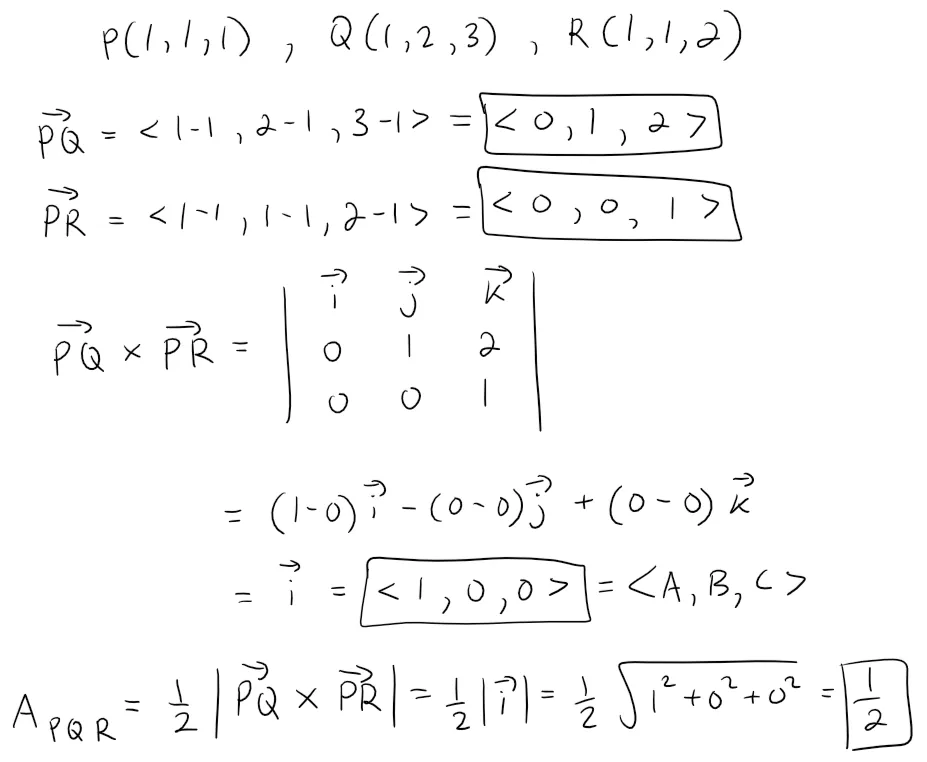
Now we can find the distance from the point S(3, -1, 2) to the plane PQR.

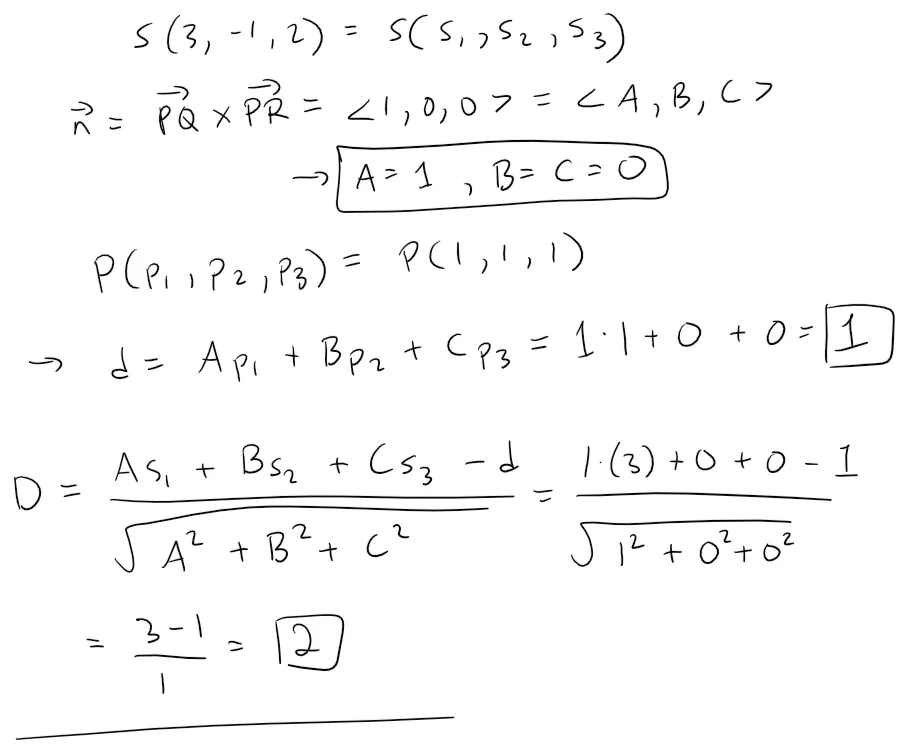
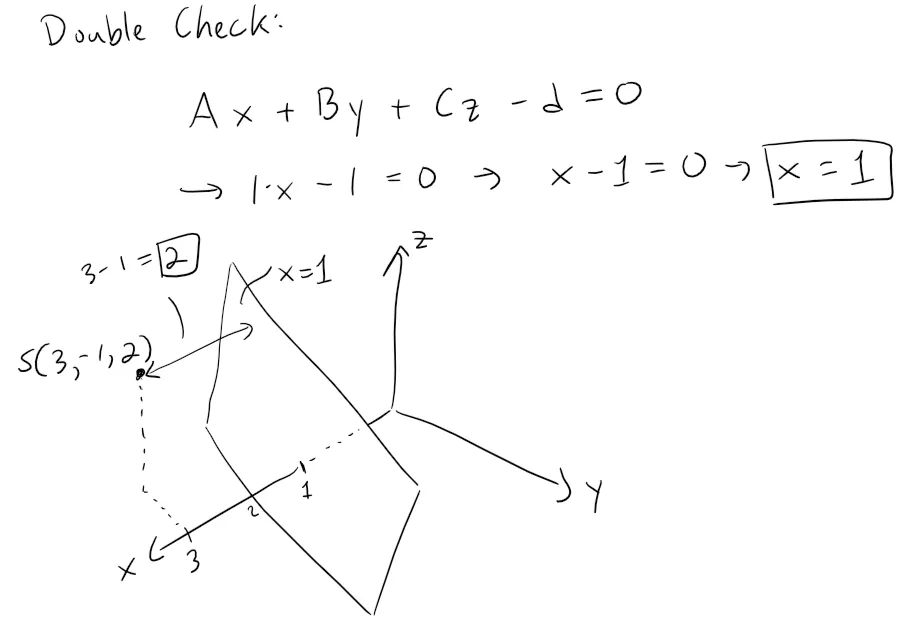
Thus the volume of the tetrahedron is:

https://www.geogebra.org/calculator/cchhtshw
Retrieved: 7 March 2023
Archive: https://archive.ph/wip/dVke2

---

Question 3

Suppose the tetrahedron in the figure has a trirectangular vertex S. (This means that the three angles at S are all right angles.)

Let A, B, and C be the areas of the three faces that meet at S, and let D be the area of the opposite face PQR.

Using the result of Problem 1, or otherwise, show that:

D² = A² + B² + C²

(This is a three-dimensional version of the Pythagorean Theorem.)

Solution:

Using the results from Question 1, the areas of the faces are: