In this video I go over further into vectors and this time look at multiplying vectors with the dot product. In my previous videos I discussed adding vectors and multiplying vectors with a scalar. This time I discuss multiplication of two vectors via the dot product, which is defined as multiplying all corresponding vector components and adding them up, thus giving a scalar or real number value; aka not a vector. Further in the video I show that this way of defining vector multiplication has useful applications since it can be reinterpreted in terms of the angle between 2 vectors. I also discuss vector projections, direction cosines, and applications to physics of the dot product.

The topics covered as well as their timestamps are listed below.

Introduction: 0:00
Sections in Calculus Book Chapter: 1:03
Topics to Cover: 1:46

The Dot Product: 2:52
- Definition 1: Dot Product: 3:38
- Example 1: 6:15
- Properties of the Dot Product: 10:49
  - Proof of Property 1: 12:42
  - Proof of Property 2: 14:00
  - Proof of Property 3: 15:59
  - Proof of Property 4: 19:15
  - Proof of Property 5: 24:00
- Geometric Interpretation of the Dot Product: 24:45
- Definition 2: Dot Product: 28:02
- Example 2: 43:14
- Corollary: 45:46
- Example 3: 46:49
- Perpendicular Vectors: 52:42
- Example 4: 54:47
Vector Angles: 56:49
- Direction Angles and Direction Cosines: 1:02:55
- Example 5: 1:17:28
Projections: Vector and Scalar Projections: 1:21:27
- Summary of Projections: 1:30:22
- Example 6: 1:33:19
Vectors in Physics: 1:39:04
- Example 7: 1:42:33
- Example 8: 1:45:25

Watch video on:

3Speak:
Odysee: https://odysee.com/@mes:8/Vectors-and-the-Geometry-of-Space-The-Dot-Product:8
BitChute:
Rumble: https://rumble.com/v21895e-vectors-and-the-geometry-of-space-the-dot-product.html
DTube:
YouTube:

Download video notes: https://1drv.ms/b/s!As32ynv0LoaIiahlV-ELBa7AO4z_vw?e=8lUKrM

View video sections playlist: https://www.youtube.com/playlist?list=PLai3U8-WIK0GbHgvpTY1mx61nTNO-Msl8

View the full Vectors and Geometry of Space video series: https://www.youtube.com/playlist?list=PLai3U8-WIK0FjJpwnxwdrOR7L8Ul8VZoZ

View Video Notes Below!

Download these notes: Link is in video description.
View these notes as an article: @mes
Subscribe via email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donate
Buy MES merchandise! https://mes.fm/store
More links: https://linktr.ee/matheasy
Follow my research in real-time on my MES Links Telegram: https://t.me/meslinks
Subscribe to MES Truth: https://mes.fm/truth

Reuse of my videos:

Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.

Fight back against censorship:

Bookmark sites/channels/accounts and check periodically

Remember to always archive website pages in case they get deleted/changed.

Recommended Books:

"Where Did the Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook

Join my forums!

Hive community: created/hive-128780

Reddit: https://reddit.com/r/AMAZINGMathStuff

Discord: https://mes.fm/chatroom

Follow along my epic video series:

#MESScience: https://mes.fm/science-playlist

#MESExperiments: @mes/list

#AntiGravity: @mes/series
-- See Part 6 for my Self Appointed PhD and #MESDuality breakthrough concept!

#FreeEnergy: https://mes.fm/freeenergy-playlist

#PG (YouTube-deleted series): @mes/videos

NOTE #1: If you don't have time to watch this whole video:

Skip to the end for Summary and Conclusions (if available)

Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed!
-- MES tutorial: @mes/play-videos-at-faster-or-slower-speeds-on-any-website

Download and read video notes.

Read notes on the Hive blockchain #Hive

Watch the video in parts.
-- Timestamps of all parts are in the description.

Browser extension recommendations:

Increase video speed: https://mes.fm/videospeed-extension

Increase video audio: https://mes.fm/volume-extension

Text to speech: https://mes.fm/speech-extension
--Android app: https://mes.fm/speech-android

Vectors and the Geometry of Space: The Dot Product

Dot Product.jpeg

Calculus Book Reference

Note that I mainly follow along the following calculus book:

Calculus: Early Transcendentals 7th Edition by James Stewart
Note: In the earlier videos I used the 6th edition.

Sections in Calculus Book Chapter

I have made a list of the sections in this particular chapter with links to the Hive post of the videos I have already finished.

Vectors and the Geometry of Space

3-D Coordinate Systems
Vectors
- Complex Numbers as Rotation Matrices
The Dot Product (Current Video)
The Cross Product
- Discovery Project: The Geometry of a Tetrahedron
Equations of Lines and Planes
- Laboratory Project: Putting 3D in Perspective
Cylinders and Quadric Surfaces
Review
- True-False Quiz
Problems Plus

Topics to Cover

Note that the timestamps will be incluhttps://1drv.ms/b/s!As32ynv0LoaIiahlV-ELBa7AO4z_vw?e=8lUKrMded in the video description for each topic listed below.

The Dot Product
- Definition 1: Dot Product
- Example 1
- Properties of the Dot Product
  - Proof of Property 1
  - Proof of Property 2
  - Proof of Property 3
  - Proof of Property 4
  - Proof of Property 5
- Geometric Interpretation of the Dot Product
- Definition 2: Dot Product
- Example 2
- Corollary
- Example 3
- Perpendicular Vectors
- Example 4
Vector Angles
- Direction Angles and Direction Cosines
- Example 5
Projections: Vector and Scalar Projections
- Summary of Projections
- Example 6
Vectors in Physics
- Example 7
- Example 8

The Dot Product

So far we have added two vectors and multiplied a vector by a scalar.

The question arises:

Is it possible to multiply two vectors so that their product is a useful quantity?

One such product is the dot product, whose definition follows.

Another is the cross product, which is discussed in a later video.

Definition 1: Dot Product

If a = <a₁, a₂, a₃> and b = <b₁, b₂, b₃>, then the dot product of a and b is the number a ⋅ b given by:

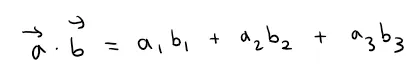
Thus, to find the dot product of a and b, we multiply the corresponding components and add.

The result is not a vector.

It is a real number, that is, a scalar.

For this reason, the dot product is sometimes called the scalar product (or inner product).

Although Definition 1 is for three-dimensional vectors, the dot product of two-dimensional vectors is defined in a similar fashion:

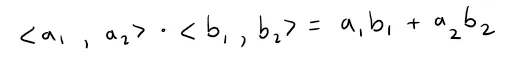
Example 1

Solution:

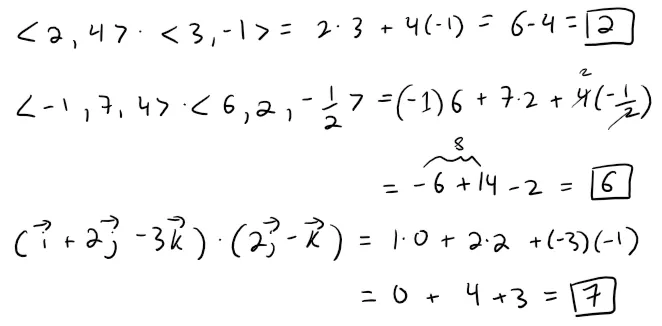
The dot product obeys many of the laws that hold for ordinary products of real numbers.

These are stated in the following theorem.

Properties of the Dot Product

If a, b, and c are vectors in V₃ and c is a scalar, then:

a ⋅ a = |a|2
a ⋅ b = b ⋅ a
a ⋅ (b + c) = a ⋅ b + a ⋅ c
(ca) ⋅ b = c(a ⋅ b) = a ⋅ (cb)
0 ⋅ b = 0

These properties are easily proved using Definition 1, and they are proved below.

Proof of Property 1

Proof of Property 2

Proof of Property 3

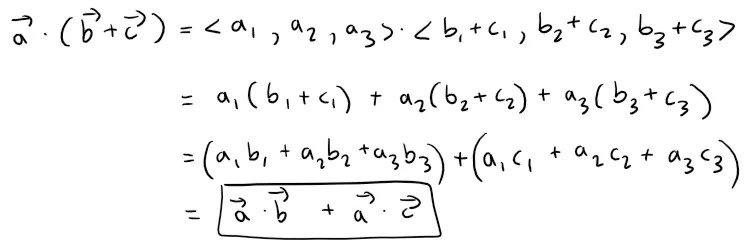
Proof of Property 4

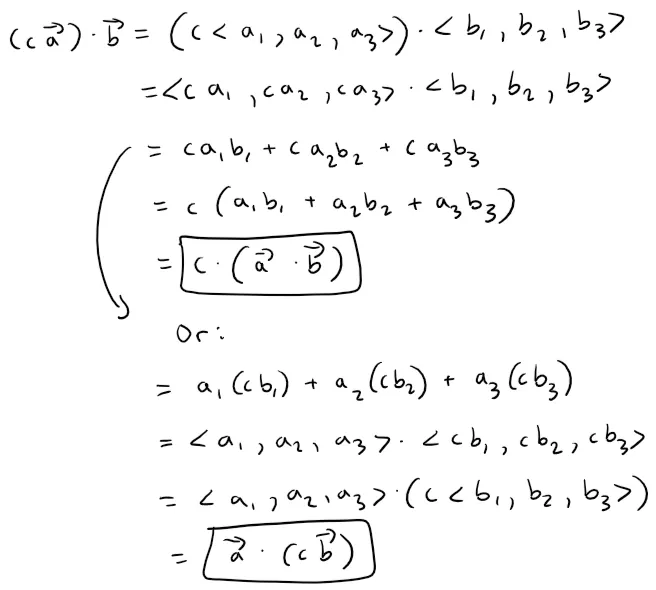
Proof of Property 5

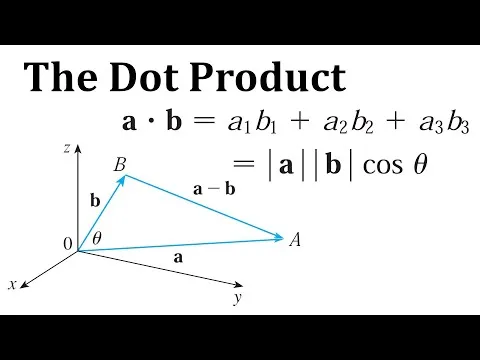
Geometric Interpretation of the Dot Product

The dot product a ⋅ b can be given a geometric interpretation in terms of the angle θ between a and b, which is defined to be the angle between the representations of a and b that start at the origin, where 0 ≤ θ ≤ π.

In other words, θ is the angle between the line segments OA and OB in the figure below.

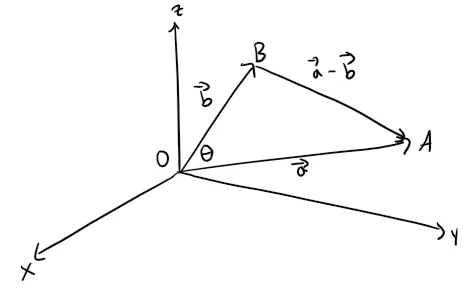
Note that if a and b are parallel vectors, the θ = 0 (both going in the same direction) or θ = π (both going in the opposite direction).

The formula in the following theorem is used by physicists as the definition of the dot product.

Definition 2: Dot Product

If θ is the angle between the vectors a and b, then:

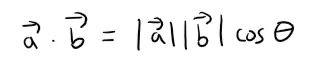
Proof:

Recall the Law of Cosines (from my earlier video).

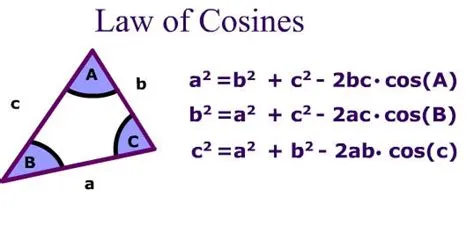
Now if we apply the Law of Cosines to the triangle OAB in the earlier figure above, we get:

Observe that the Law of Cosines still applies in the limiting cases when θ = 0 or π, or a = 0 or b = 0.

For example, when θ = 0:

Since |OA| = |a|, |OB| = |b|, and |AB| = |a - b|, the above equation becomes:

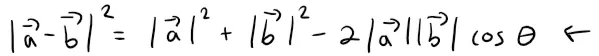
Using Properties 1, 2, and 3 of the dot product, we can rewrite the left side of this equation as follows:

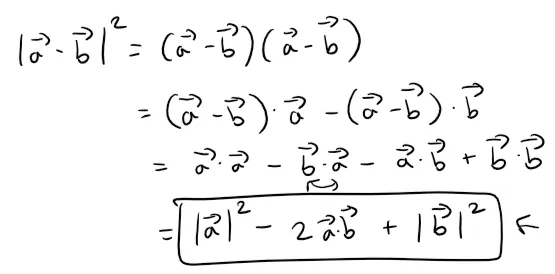
Thus putting the two equations together we have:

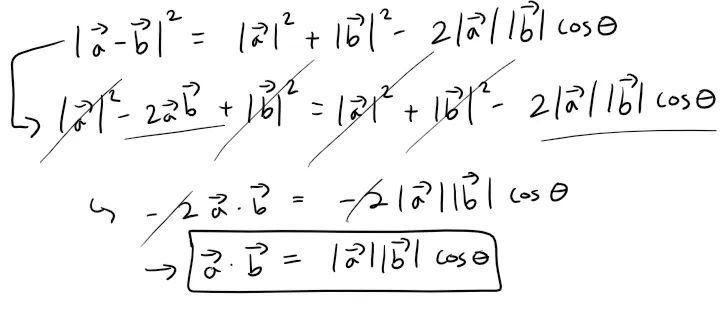
Example 2

If the vectors a and b have lengths 4 and 6, and the angle between them is π/3, find a ⋅ b.

Solution:

Using the alternative definition of the dot product, Definition 2, we have:

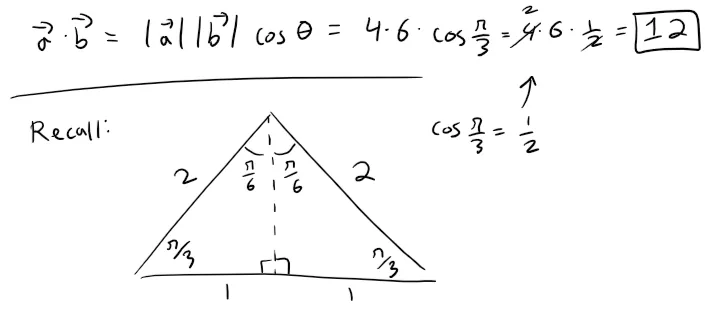
The alternative dot product formula allows us to find the angle between two vectors.

Corollary

If θ is the angle between the nonzero vectors a and b, then:

Example 3

Find the angle between the vectors a = <2, 2, -1> and b = <5, -3, 2>.

Solution:

Let's solve all the terms of the Corollary formula.

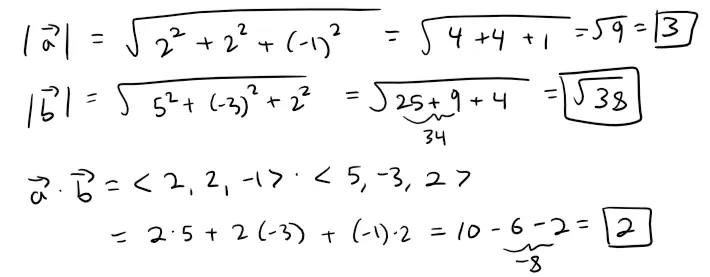
So the angle between a and b is:

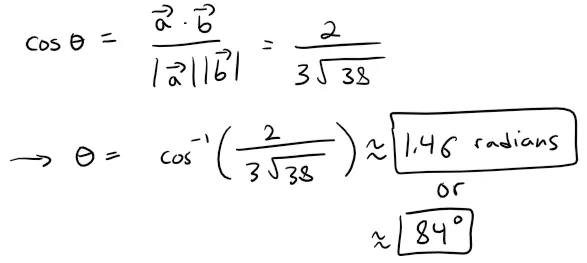
Calculation Check:

acos(2/(3*sqrt(38))) = 83.79145537381417 degrees.

83.79145537381417 * pi / 180 = 1.462436781310953 radians.

Perpendicular Vectors

Two nonzero vectors a and b are called perpendicular or orthogonal if the angle between them is θ = π/2.

Then the alternative dot product formula becomes:

And conversely if a ⋅ b = 0, then cos θ = 0, so θ = π/2.

The zero vector 0 is considered to be perpendicular to all vectors.

Therefore we have the following method for determining whether two vectors are orthogonal.

Two vectors a and b are orthogonal if and only if a ⋅ b = 0.

Example 4

Show that if 2i + 2j - k is perpendicular to 5i - 4j + 2k.

Solution:

Determining the dot product we get:

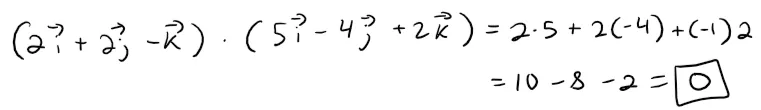
Thus, these vectors are perpendicular by the earlier theorem.

Vector Angles

Because cos θ > 0 if 0 ≤ θ ≤ π/2 and cos θ < 0 if π/2 < θ ≤ π, we see that a ⋅ b is positive for θ < π/2 and negative for θ > π/2.

We can think of a ⋅ b as measuring the extent to which a and b point in the same direction.

The dot product a ⋅ b is positive if a and b point in the same general direction, 0 if they are perpendicular, and negative if they point in generally opposite directions; as illustrated below.

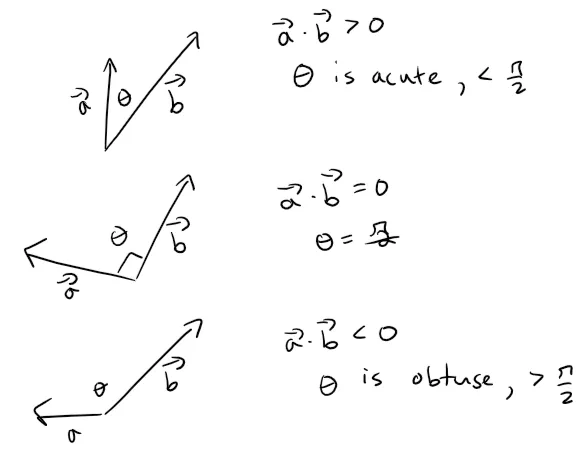
In the extreme case where a and b point in exactly the same direction, we have θ = 0, so cos θ = 1 and:

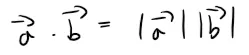
If a and b point in exactly opposite directions, then θ = π and so cos θ = -1 and a ⋅ b = - |a||b|.

Direction Angles and Direction Cosines

The direction angles of a nonzero vector a are the angles α, β, and γ (in the [0, π]) that a makes with the positive x-, y-, and z-axes; see the figure below.

The cosines of these direction angles, cos α, cos β, and cos γ are called the direction cosines of the vector a.

Using the earlier Corollary with b replaced by i, we obtain:

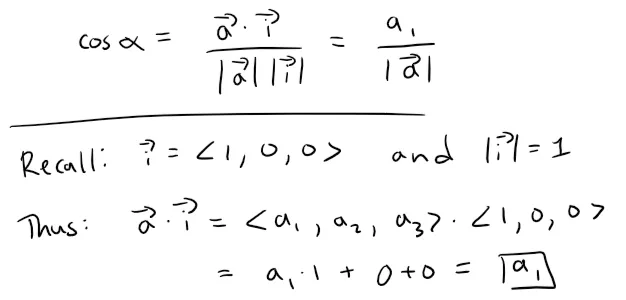
This can also be seen directly form the earlier figure.

Similarly, we also have:

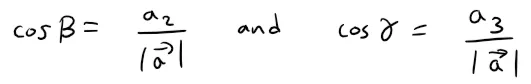
By squaring and adding the above direction cosines, we see that:

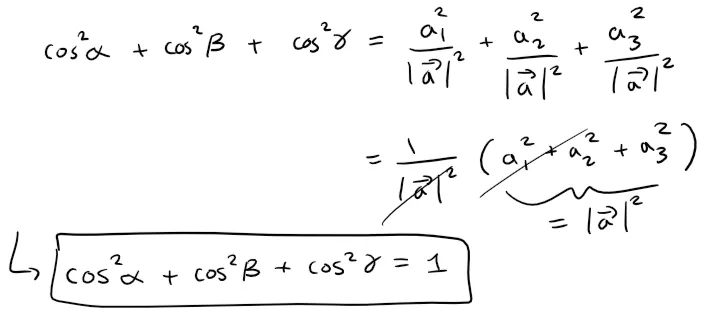
We can also use the direction cosines to write:

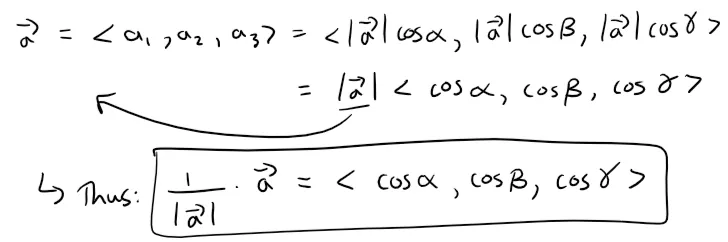
This equation says that the direction cosines of a are the components of the unit vector in the direction of a.

Example 5

Find the angles of the vector a = <1, 2, 3>.

Solution:

Calculation Check:

acos(1/sqrt(14)) = 74.498640433063 degrees.
acos(2/sqrt(14)) = 57.68846676257615 degrees.
acos(3/sqrt(14)) = 36.69922520048987 degrees.

Projections: Vector and Scalar Projections

The figure below shows PQ and PR of two vectors a and b with the same initial point.

If S is the foot of the perpendicular line from R to the line containing PQ, then the vector with representation PS is called the vector projection of b onto a and is denoted by proj_a b. (You can think of it as a shadow of b).

The scalar projection of b onto a (also called the component of b along a) is defined to be the signed magnitude of the vector projection, which is the number |b|cos θ, where θ is the angle between a and b; see the figure below. This is denoted by comp_a b.

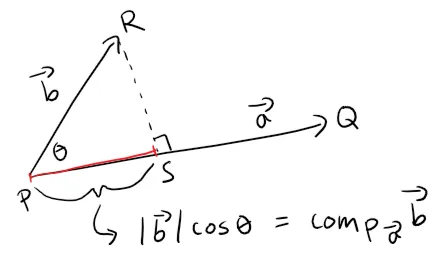
Observe that comp_a b is negative if π/2 < θ ≤ π.

The equation:

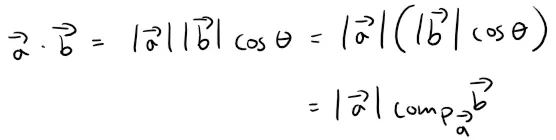
shows that the dot product of a and b can be interpreted as the length of a times the scalar projection of b onto a.

Since:

then the component of b along a can be computed by taking the dot product of b with the unit vector in the direction of a.

We summarize these ideas as follows:

Summary of Projections

Scalar projection of b onto a:

Vector projection of b onto a:

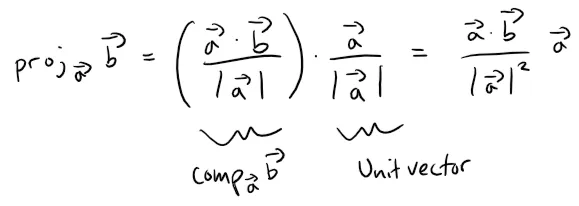
Notice that the vector projection is the scalar projection times the unit vector in the direction of a.

Example 6

Find the scalar projection and vector projection of b = <1, 1, 2> onto a = <-2, 3, 1>.

Solution:

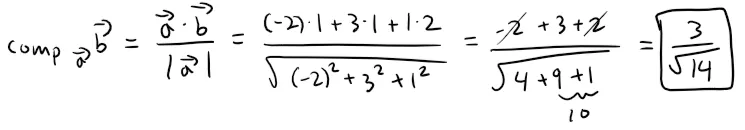
The vector projection is this scalar projection times the unit vector in the direction of a:

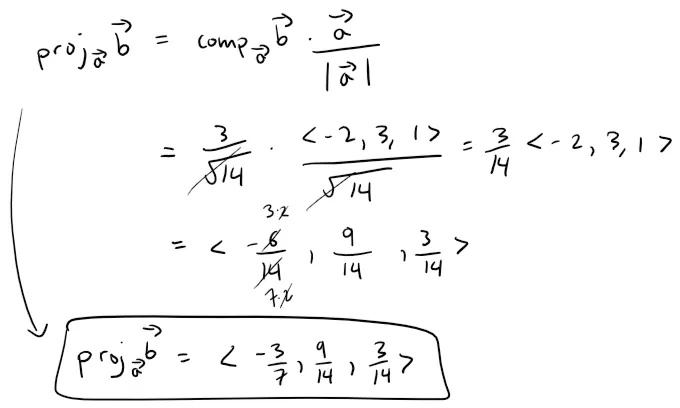
Vectors in Physics

One use of projections occurs in physics in calculating work.

In my earlier video, we defined the work done by a constant force F in moving an object through a distance d as W = Fd, but this applies only when the force is directed along the line of motion of the object.

Suppose, however, that the constant force is a vector F = PR pointing in some other direction, as in the figure below.

If the force moves the object from P to Q, then the displacement vector is D = PQ.

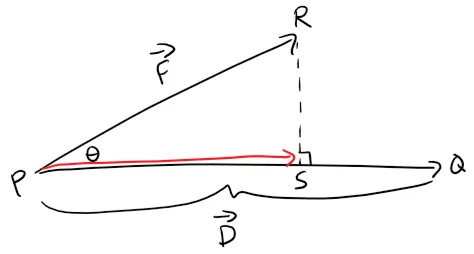
The work done by this force is defined to be the product of the component of the force along D and the distance moved:

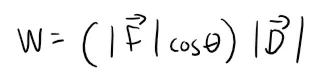
But then, from Definition 2, we have:

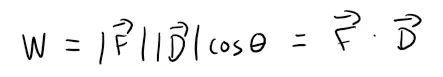
Thus the work done by a constant force F is the dot product F ⋅ D, where D is the displacement vector.

Example 7

A wagon is pulled a distance of 100 m along a horizontal path by a constant force of 70 N.

The handle of the wagon is held at an angle of 35° above the horizontal.

Find the work done by the force.

Solution:

If F and D are the force and displacement vectors, as pictured in the figure below, then the work done is:

Calculation Check:

70100cos(35) = 5,734.064310022943

Example 8

A force is given by a vector F = 3i + 4j + 5k and moves a particle from the point P(2, 1, 0) to the point Q(4, 6, 2).

Find the work done.

Solution:

The displacement vector is:

Thus the work done is:

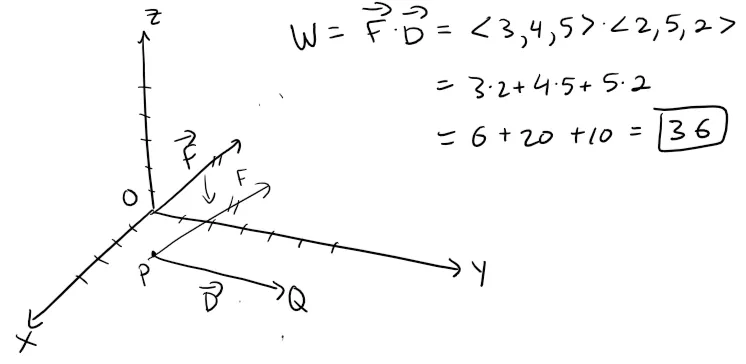
If the unit of length is meters and the magnitude of the force is measured in newtons, then the work done is 36 Joules.