Infinite Sequences and Series: Representations of Functions as Power Series

72
5 years ago
in
#mathematics

In this video I go over further into infinite sequences and series; and in particular expand upon my earlier video on power series. This time I show how we can represent many functions as power series as well as go over a theorem that allows for differentiation and integration of power series term by term. This theorem, as well as this overall concept of representing functions as power series is one of the most important concepts in all of science because it allows for much easier computation of many different functions. In fact many computers and calculators use this technique behind the scenes since they are often much easier to deal with than trying to find exact integrals or derivatives which many times are not simple.

In this video, and at the second half of this video, I also go over an extensive 2 hour long proof of the theorem for term-by-term differentiation and integration of power series. Although this proof is extensive, after searching all over online for the proof, I believe my proof may in fact be the most clear and understandable. Let me know if it helps!

The topics covered in this video are listed below with their time stamps.

  1. @ 2:24 - Representation of Functions as Power Series
    • @ 3:17 - Equation 1
    • @ 10:48 - Example 1
    • @ 26:35 - Example 2
    • @ 30:16 - Example 3
    • @ 37:06 - Differentiation and Integration of Power Series
    • @ 38:09 - Theorem 1: Term by Term Differentiation and Integration
    • @ 50:50 - Example 4
    • @ 54:18 - Example 5
    • @ 58:36 - Example 6
    • @ 1:11:02 - Example 7: Gregory's Series
      • @ 1:25:59 - Leibniz Formula for π
    • @ 1:30:30 - Example 8
  3. Exercises
    • @ 2:11:57 - Exercise 1
    • @ 1:55:34 - Exercise 2
    • @ 2:26:11 - Exercise 3: Proof of Theorem 1
      • @ 2:32:29 - Lemma
        • @ 2:34:58 - Lemma Derivative Proof
        • @ 3:01:16 - Lemma Integral Proof
      • @ 3:08:59 - Theorem 1 Using z = (x - a)
        • @ 3:12:41 - Theorem 1a Derivative Proof
          • @ 3:24:59 - Brief Overview of the Binomial Theorem
        • @ 3:57:33 - Theorem 1b Integral Proof

Watch Video On:

Download Video Notes: https://1drv.ms/b/s!As32ynv0LoaIh_17muwohTwCBpQ45Q?e=pldHwj

View Video Notes Below!

Download These Notes: Link is in Video Description.
View These Notes as an Article: @mes
Subscribe via Email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donate

Reuse of My Videos:

  • Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.

Fight Back Against Censorship:

  • Bookmark sites/channels/accounts and check periodically
  • Remember to always archive website pages in case they get deleted/changed.

Join my private Discord Chat Room: https://mes.fm/chatroom

Check out my Reddit and Voat Math Forums:

Buy "Where Did The Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
Follow along my epic video series:

NOTE #1: If you don't have time to watch this whole video:

NOTE #2: If video volume is too low at any part of the video:

Infinite Sequences and Series: Representations of Functions as Power Series

Functions as Power Series.jpeg

Calculus Book Reference

Note that I mainly follow along the following calculus book:

  • Calculus: Early Transcendentals Sixth Edition by James Stewart

Topics to Cover

  1. Representation of Functions as Power Series
    • Equation 1
    • Example 1
    • Example 2
    • Example 3
  2. Differentiation and Integration of Power Series
    • Theorem 1: Term by Term Differentiation and Integration
    • Example 4
    • Example 5
    • Example 6
    • Example 7: Gregory's Series
      • Leibniz Formula for π
    • Example 8
  3. Exercises
    • Exercise 1
    • Exercise 2
    • Exercise 3: Proof of Theorem 1
      • Lemma
        • Lemma Derivative Proof
        • Lemma Integral Proof
      • Theorem 1a Derivative Proof
        • Brief Overview of the Binomial Theorem
      • Theorem 1b Integral Proof

Representation of Functions as Power Series

In this section we learn how to represent certain types of functions as sums of power series by manipulating geometric series or by differentiating or integrating such a series.

You might wonder why we would ever want to express a known function as a sum of infinitely many terms.

We will see later that this strategy is useful for integrating functions that don't have elementary antiderivatives, for solving differential equations, and for approximating functions by polynomials.

Scientists do this to simplify the expressions they deal with; computer scientists do this to represent functions on calculators and computers.

We start with an equation that we have seen before:

Equation 1

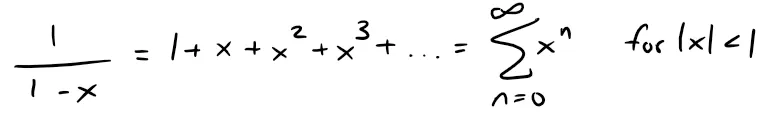
We first encountered this equation in Example 5 of my earlier video on Infinite Series and shown below, where we obtained it by observing that it is a geometric series with a = 1 and r = x.

@mes/infinite-series-definition-examples-geometric-series-harmonics-series-telescoping-sum-more

Retrieved: 27 July 2019
Archive: http://archive.fo/FGAyJ

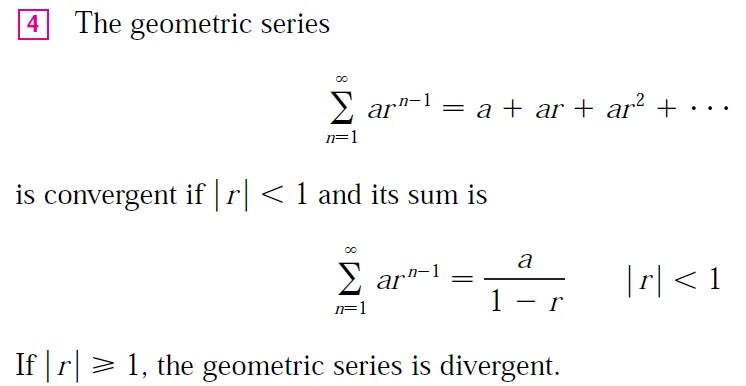
But here our point of view is different.

We now regard Equation 1 as expressing the function f(x) = 1/(1 - x) as a sum of a power series.

Because the sum of a series is the limit of the sequence of partial sums, we have:

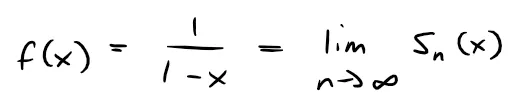
where:

is the n-th partial sum.

A geometric illustration of Equation 1 and some partial sums is shown in the following figure.

https://www.desmos.com/calculator/9awpqmhxfd

Retrieved: 19 December 2019
Archive: https://archive.ph/VaGiu

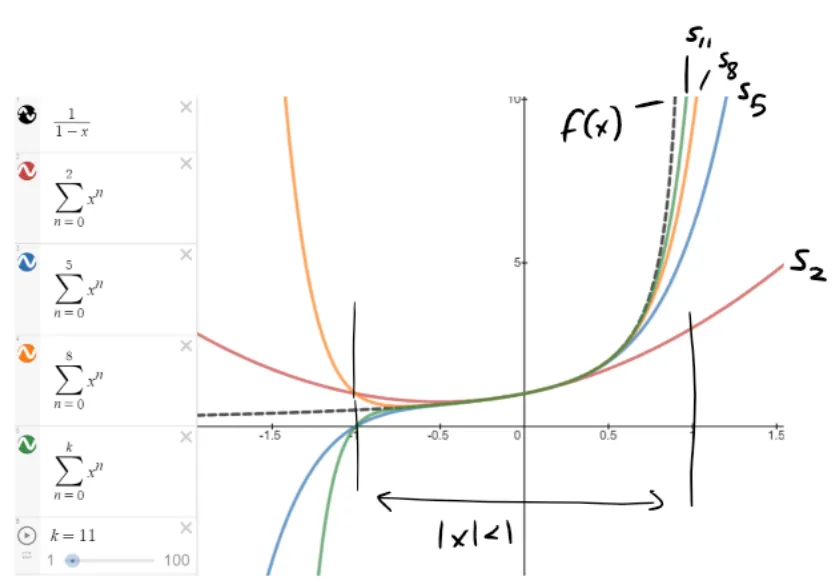
Notice that as n increases, sn(x) becomes a better approximation to f(x) for -1 < x < 1.

Example 1

Express 1/(1 + x2) as the sum of a power series and find the interval of convergence.

Solution:

Replacing x by -x2 in Equation 1, we have:

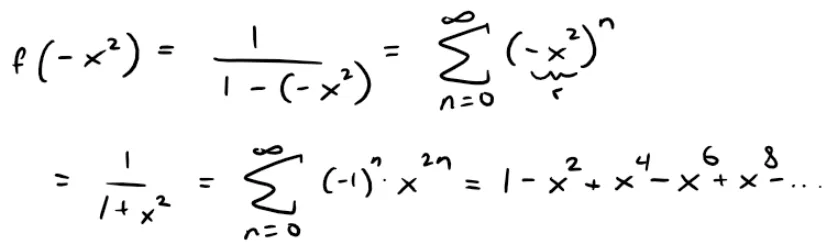
Because this is a geometric series, it converges when:

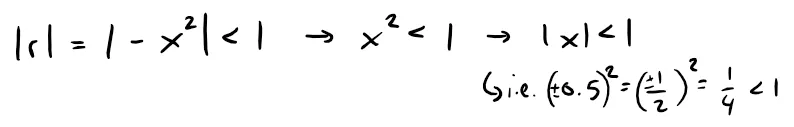
Therefore the interval of convergence is (-1, 1).

Of course, we could have determined the Radius (or interval) of Convergence by applying the Ratio Test, but that much work is unnecessary here.

Nonetheless, we will solve it again using the Ratio Test so here is a quick recap on the Radius of Convergence, the Interval of Convergence and the Ratio Test:

@mes/infinite-sequences-and-series-power-series

Retrieved: 19 December 2019
Archive: https://archive.ph/kAeuV

@mes/infinite-sequences-and-series-absolute-convergence-and-the-ratio-root-tests

Retrieved: 17 September 2019
Archive: http://archive.fo/ANfgj

Thus, using the ratio test we have:

Thus, by the Ratio Test, the given power series converges when x2 < 1, or |x|< 1; thus the interval of convergence could be (-1, 1), [-1, 1), (-1, 1], or [-1, 1]; i.e. we have to check the endpoints.

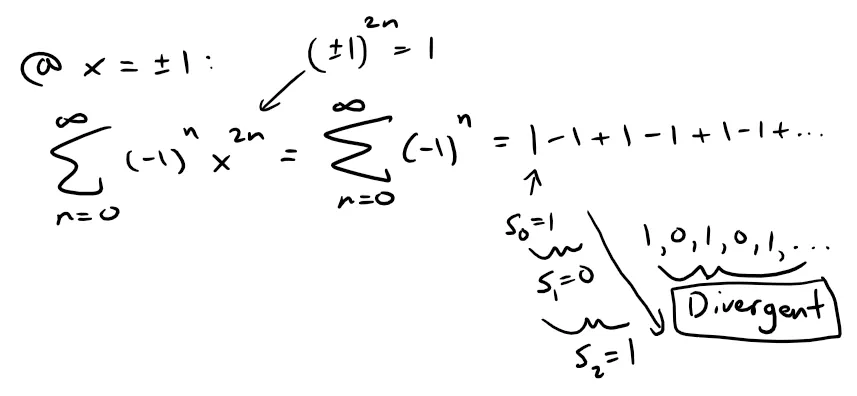
Therefore, the interval of convergence is (-1, 1).

Example 2

Find a power series representation for 1/(x + 2).

Solution:

In order to put this function in the form of the left side of Equation 1 we first factor a 2 from the denominator:

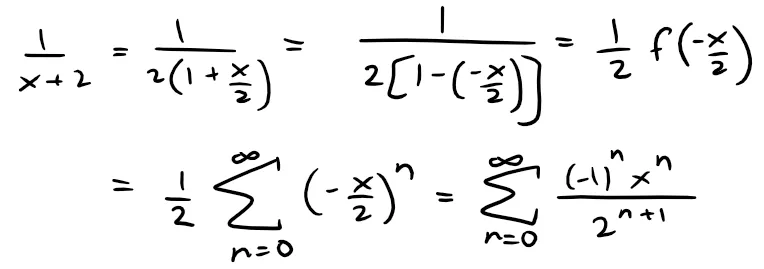
This (geometric) series converges when:

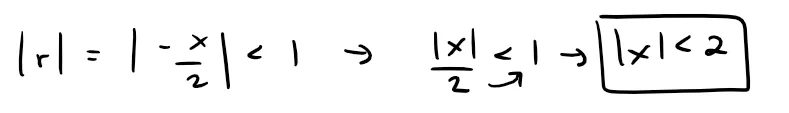
So the interval of convergence is (-2, 2).

Example 3

Find a power series representation of x3/(x + 2).

Solution:

Since this function is just x3 times the function in Example 2, all we have to do is multiply that series by x3:

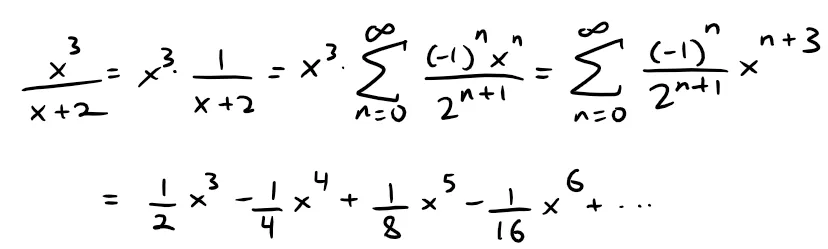
Since the first term has a x3, then another way of writing this series is as follows:

As in Example 2, the interval of convergence is (-2, 2) since we are merely multiplying it by a constant when we set x to be any value (in the interval of convergence).

Note that it's legitimate to move x3 across the sigma sign because it doesn't depend on n; as in the following theorem (part i) from my earlier video but with c = x3.

@mes/infinite-series-definition-examples-geometric-series-harmonics-series-telescoping-sum-more

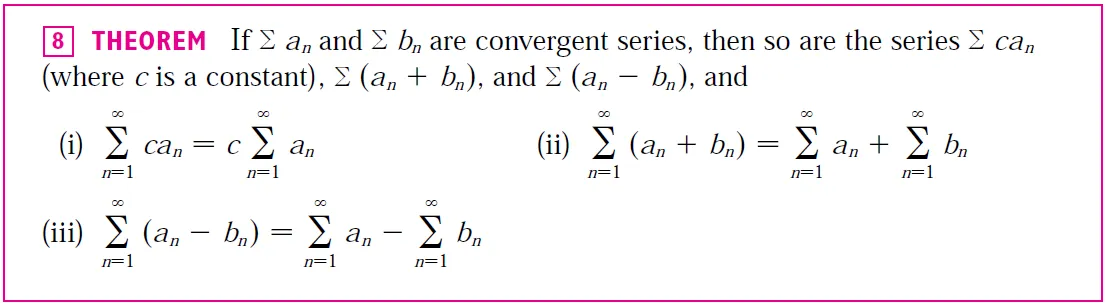
Differentiation and Integration of Power Series

The sum of a power series is a function:

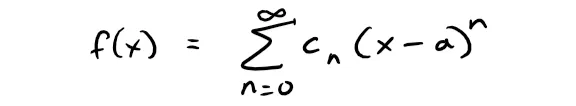
whose domain is the interval of convergence of the series.

We would like to be able to differentiate and integrate such functions, and the following theorem (which I prove at the end of this video in Exercise 3) says that we can do so by differentiating or integrating each individual term in the series, just as we would for a polynomial.

This is called term-by-term differentiation and integration.

Theorem 1: Term by Term Differentiation and Integration

If the power series ∑ cn(x - a)n has a radius of convergence R > 0, then the function f defined by:

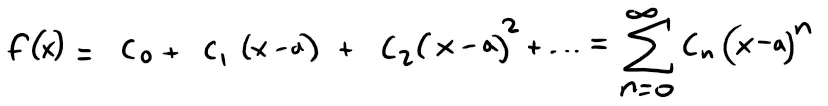
is differentiable (and therefore continuous) on the interval (a - R, a + R) and:

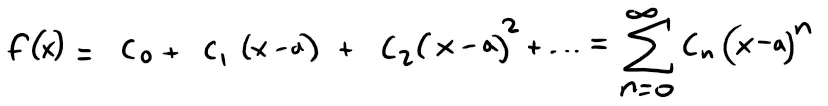
The radii of convergence of the power series in Equations (i) and (ii) are both R.

In part (ii), the integral of the first term c0 is rewritten so that all the terms have the same form:

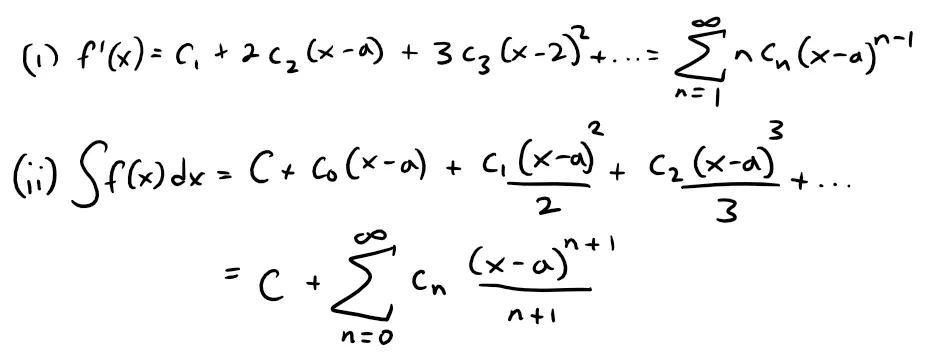
Also note that each term when integrated has its own integration constant but the summation of them all is just a constant itself, so we will just leave it as C.

NOTE 1

Equations (i) and (ii) in Theorem 1 can be rewritten in the form:

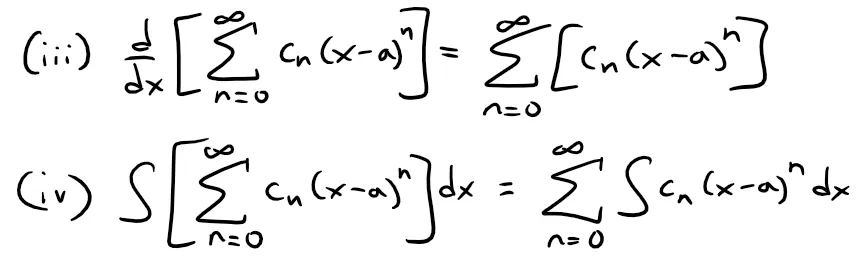
We know that, for finite sums, the derivative of a sum is the sum of the derivatives and the integral of a sum is the sum of integrals.

Equations (iii) and (iv) assert that the same is true for infinite sums, provided we are dealing with power series.

For other types of series of functions the situation is not as simple; see Exercise 1 at the end of this video.

NOTE 2

Although Theorem 1 says that the radius of convergence remains the same when a power series is differentiated or integrated, this does not means that the interval of convergence remains the same.

It may happen that the original series converges at an endpoint, whereas the differentiated series diverges there; see Exercise 2 at the end of this video.

NOTE 3

The idea of differentiating a power series term by term is the basis for a powerful method for solving differential equations; which I will look to discuss this method in future videos.

Also note from my earlier video that if a function is differentiable then it is continuous:

Retrieved: 22 December 2019
Archive: https://archive.ph/wip/w483w

EXAMPLE 4

In my earlier video (shown below), we saw that the Bessel function:

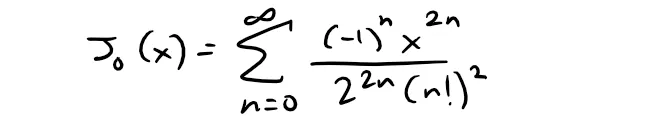
is defined for all x.

@mes/infinite-sequences-and-series-power-series

Thus, by Theorem 1, J0 is differentiable for all x and its derivative is found by term-by-term differentiation as follows:

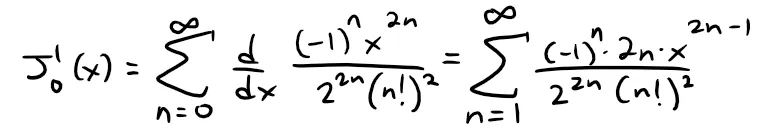
Example 5

Express 1/(1 - x)2 as a power series by differentiating Equation 1. What is the radius of convergence?

Solution:

Differentiating each side of the equation:

we get:

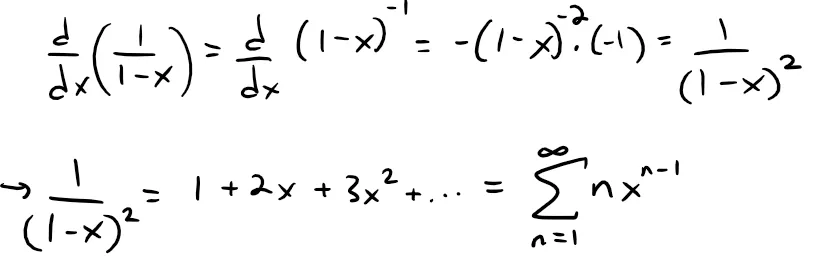
If we wish, we can replace n by n + 1 and write the answer as:

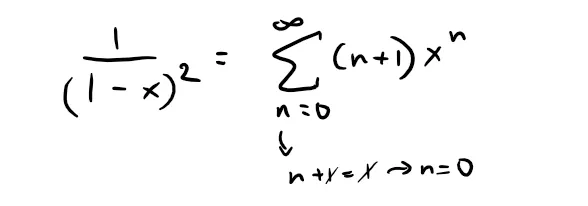
According to Theorem 1, the radius of convergence of the differentiated series is the same as the radius of convergence of the original series, namely, R = 1.

Example 6

Find a power series representation of ln(1 - x) and its radius of convergence.

Solution:

We notice that, except for a factor of -1, the derivative of this function is 1/(1 - x).

Recall the derivative of ln(x) from my earlier video:

Retrieved: 20 December 2019
Archive: https://archive.ph/wip/Qj7ux

Thus we have:

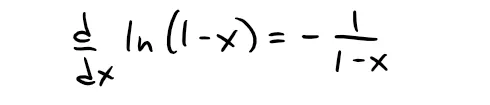
So we integrate both sides of Equation 1:

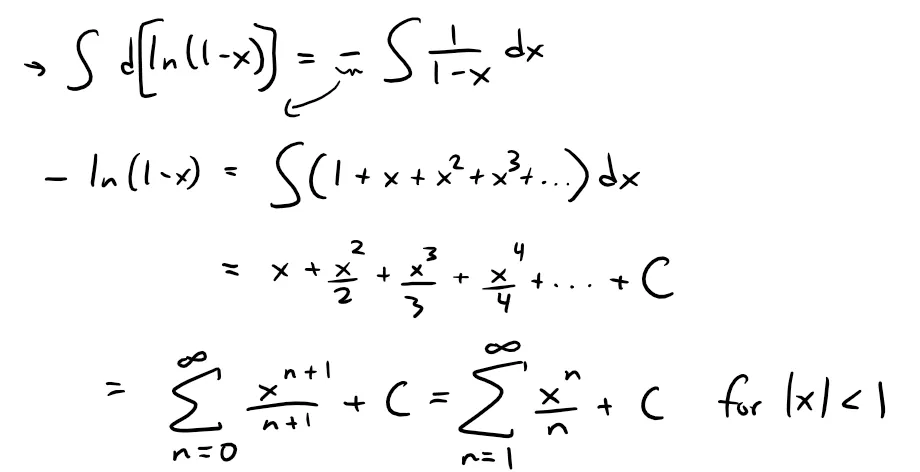
To determine the value of C we put x = 0 in this equation and obtain:

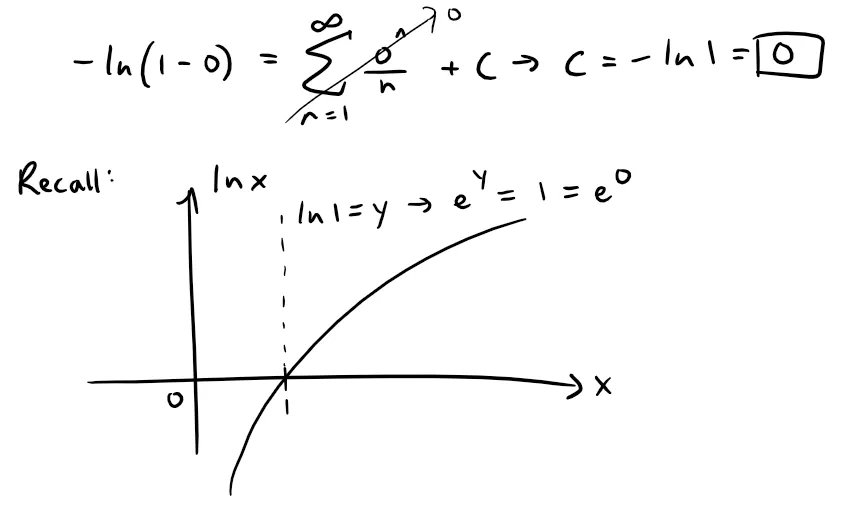
Thus, moving the negative sign over to the other side, we have:

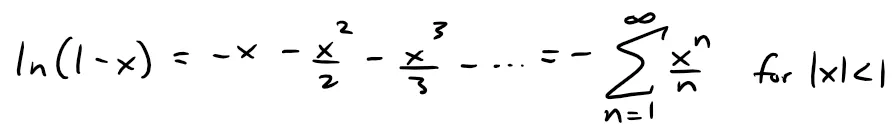
The radius of convergence is the same as for the original series: R = 1.

Notice what happens if we put x = 1/2 in the result of Example 6.

Since:

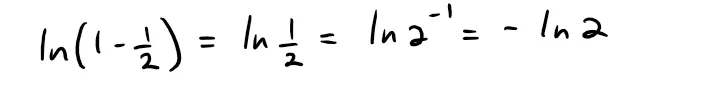
we see that:

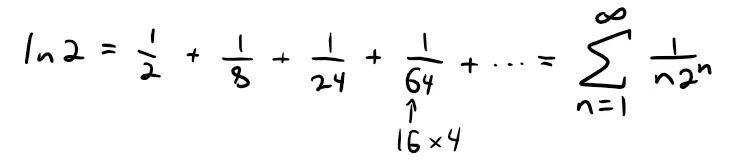
Example 7: Gregory's Series

Find a power series representation for f(x) = tan-1x

Solution:

We observe that f'(x) = 1/(1 + x2), proved in my earlier video shown below, and find the required series by integrating the power series for 1/(1 + x2) found in Example 1.

Retrieved: 20 December 2019
Archive: https://archive.ph/c5VBV

Thus, from Example 1:

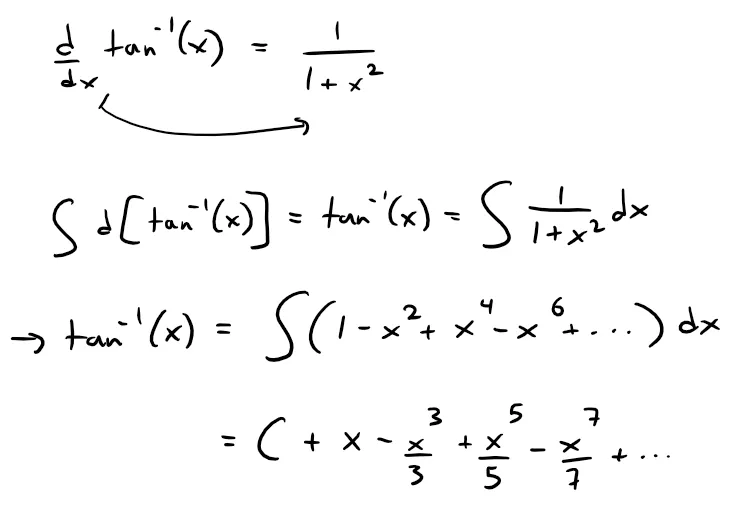
To find C we put x = 0 and obtain C = tan-10 = 0.

Therefore:

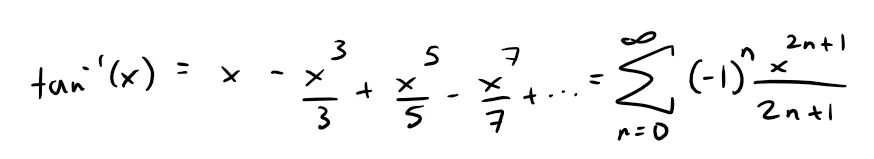
Since the radius of convergence of the series for 1/(1 + x2) is 1, the radius of convergence of this series for tan-1x is also 1.

Gregory's Series

The power series for tan-1 x obtained in Example 7 is called Gregory's series after the Scottish mathematician James Gregory (1638 - 1675), who had anticipated some of Newton's discoveries.

We have shown that Gregory's series is valid when -1 < x < 1, but it turns out that it is also valid when x ± 1; my calculus book doesn't prove this so I have proved it below.

Note that I first tried proving this using the Ratio, Root, and Integral Tests but the results were inconclusive.

The Alternating Series Test, referenced below from my earlier video, however, proved fruitful.

@mes/infinite-sequences-and-series-alternating-tests

Retrieved: 26 August 2019
Archive: http://archive.fo/9neM8

Consider the case where x = 1:

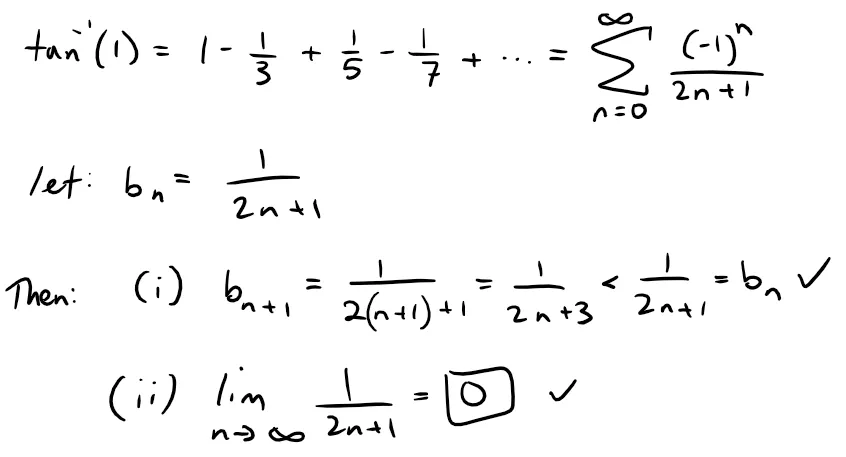
Thus the series converges by the A.S.T.

For x = - 1:

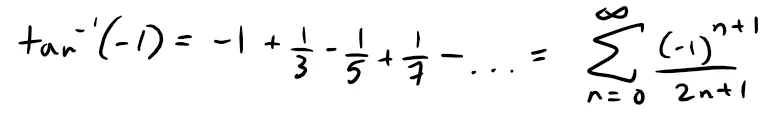
This is the same series but the signs are changed hence bn remains the same and the series converges by the A.S.T.

Leibniz formula for π

Notice that when x = 1 the series becomes:

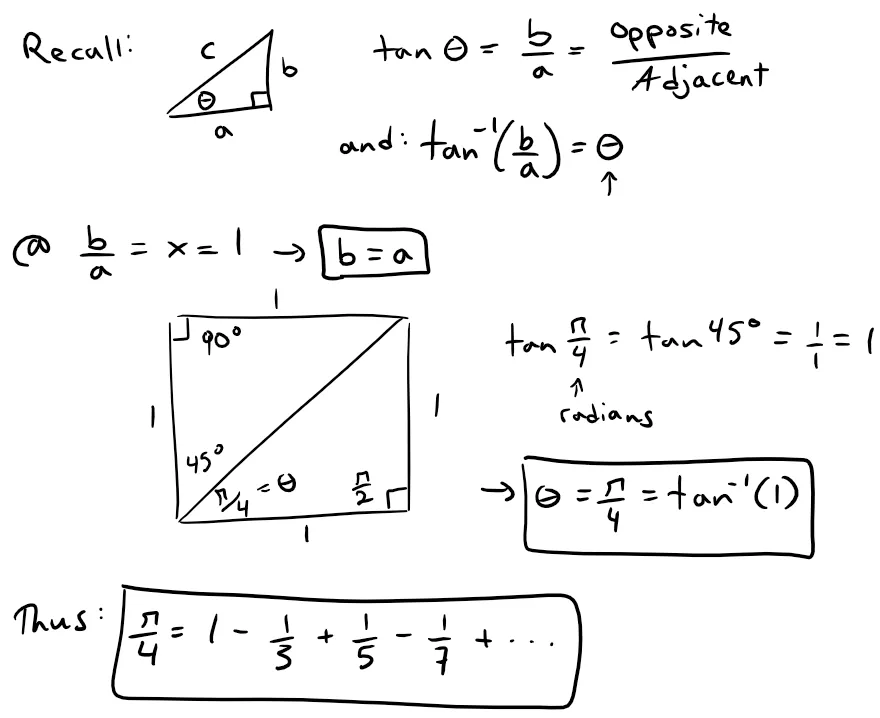
This beautiful result is known as the Leibniz formula for π.

Example 8:

(a) Evaluate the following integral as a power series:

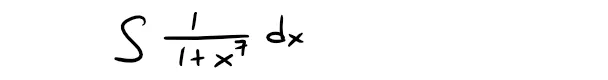
(b) Use part (a) to approximate the following definite integral correct to within 10-7:

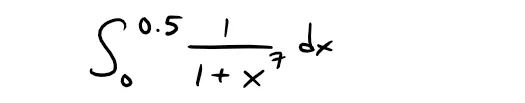
Solution:

(a) The first step is to express the integrand, 1/(1 + x7), as the sum of a power series.

As in Example 1, we start with Equation 1 and replace x by -x7:

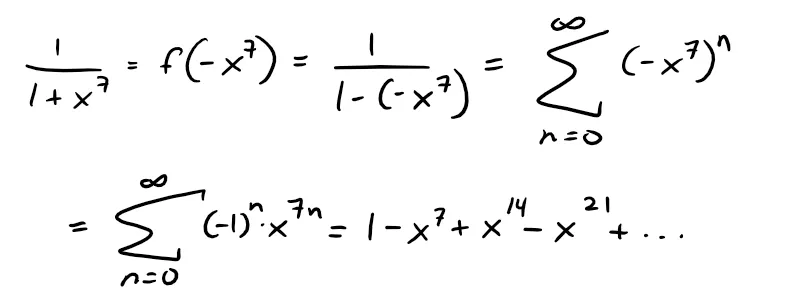
Now we integrate term by term:

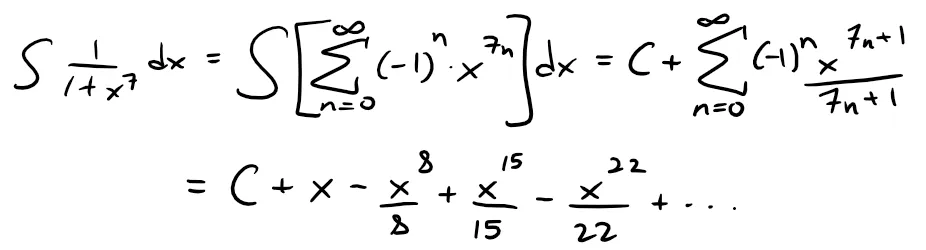
By Theorem 1, this series converges for:

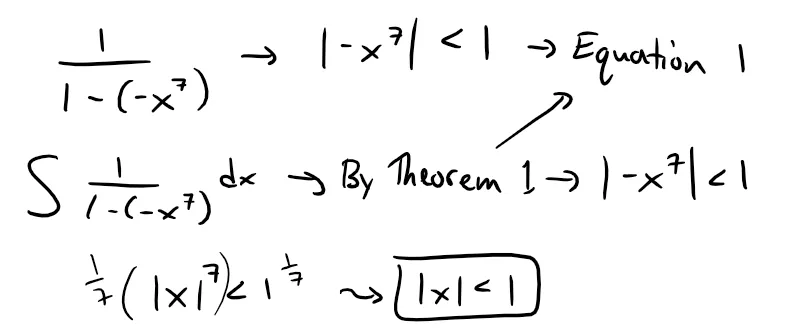
(b) In applying the Fundamental Theorem of Calculus (referenced below from my earlier videos), it doesn't matter which anti-derivative we use, so let's use the antiderivative from part (a) with C = 0:

Retrieved: 20 December 2019
Archive: https://archive.ph/wip/Bd7wE

Retrieved: 20 December 2019
Archive: https://archive.ph/wip/AbsvX

Therefore:

This infinite series is the exact value of the definite integral, but since it is an alternating series, we can approximate the sum using the Alternating Series Estimation Theorem; and referenced below also from my earlier video.

@mes/infinite-sequences-and-series-alternating-tests

If we stop adding after the term with n = 3, the error is smaller than the term with n = 4:

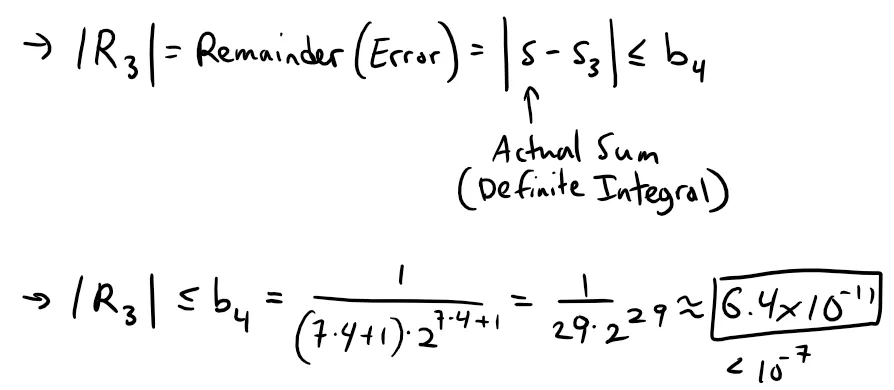
https://duckduckgo.com/?q=1%2F(29*2%5E29)&t=h_&ia=calculator

Retrieved: 19 December 2019
Archive: https://archive.ph/DEcpS

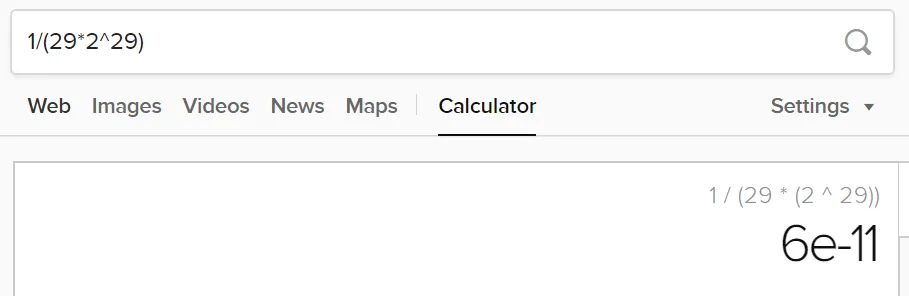
So we have:

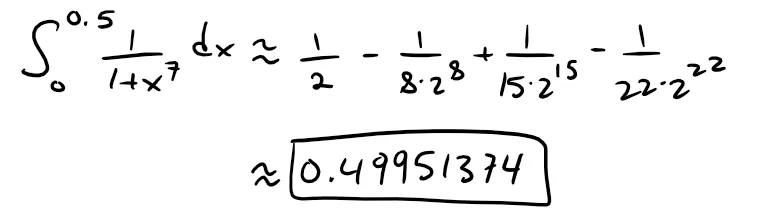
Calculation Check:

  • 1/2 - 1/(8·2^8) + 1/(15·2^15) - 1/(22·2^22) = 0.4995

This example demonstrates one way in which power series representations are useful.

Integrating 1/(1 + x7) by hand is incredibly difficult.

Different computer algebra systems (CAS) return different forms of the answer, but they are all extremely complicated; a few examples of CAS computations are shown below.

https://www.integral-calculator.com/

Retrieved: 19 December 2019
Archive: Not Available

Yeah…. I'll stick to power series for these integrals LOL

https://www.wolframalpha.com/input/?i=1%2F%281%2Bx%5E7%29

Retrieved: 19 December 2019
Archive: https://archive.ph/v04Nz

The infinite series answer that we obtained in Example 8 (a) is actually much easier to deal with than the finite answer provided by a Computer Algebra System (CAS).

Exercises

Exercise 1

Let fn(x) = (sin nx)/n2, show that the series ∑ fn(x) converges for all values of x but the series of derivatives ∑ f’n(x) diverges when x = 2kπ, where k is an integer.

For what values of x does the series ∑ f'‘n(x) converge?

Solution:

Note that:

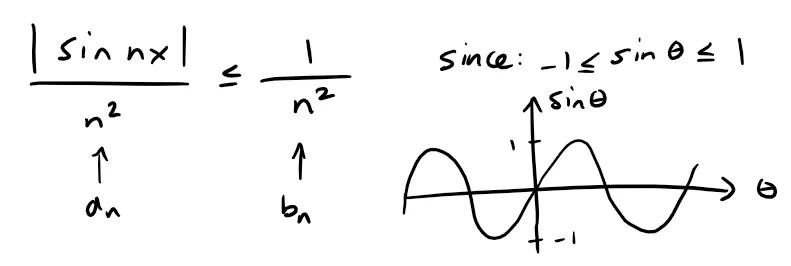
Since ∑ 1/n2 is a convergent p-series with p = 2 > 1, then by applying the Comparison Test, then ∑ fn(x) is absolutely convergent, and therefore convergent for all values of x; the following references highlight the relevant portions of my earlier videos.

@mes/infinite-sequences-and-series-the-integral-test-and-estimate-of-sums

Retrieved: 26 August 2019
Archive: http://archive.fo/vapHa

@mes/infinite-sequences-and-series-the-comparison-tests

Retrieved: 26 August 2019
Archive: http://archive.fo/f0SM5

@mes/infinite-sequences-and-series-absolute-convergence-and-the-ratio-root-tests

Retrieved: 17 September 2019
Archive: http://archive.fo/ANfgj

The follow theorem follows from the Comparison Test (note that the reverse may not be true):

Taking the derivative of fn(x) we get:

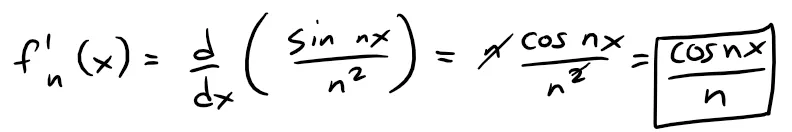
Thus when x = 2kπ [k an integer], we have:

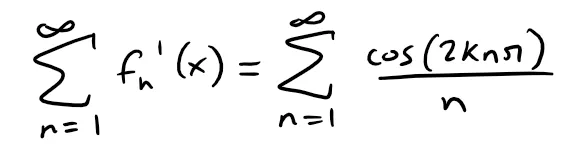
Note that 2knπ are just integer multiples of 2π, that is cos(2knπ) = 1.

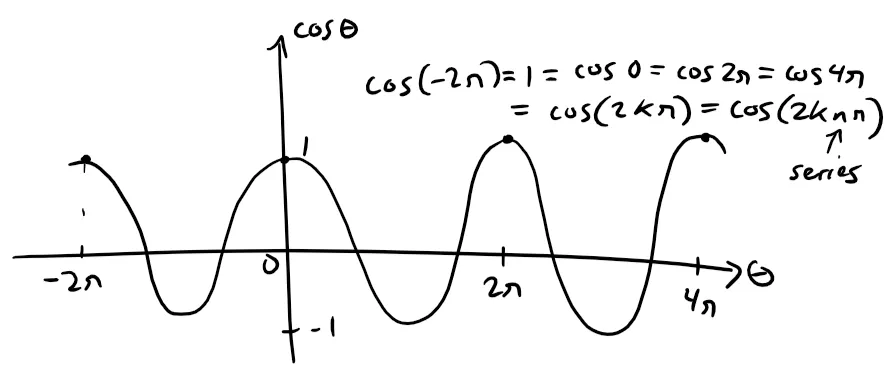
Thus, at x = 2kπ, i.e. at any integer multiple of 2π, the series ∑ f’n(x) becomes the divergent harmonic series (p = 1) and thus diverges:

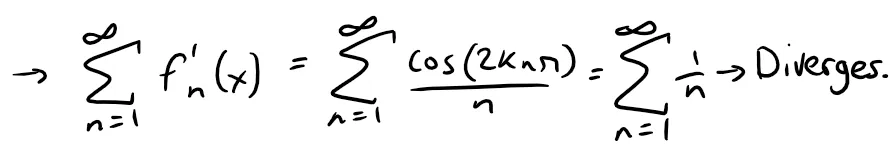
The second derivative is:

And this converges only if sin nx = 0, or x = kπ [k an integer]; that is any integer multiple of π.

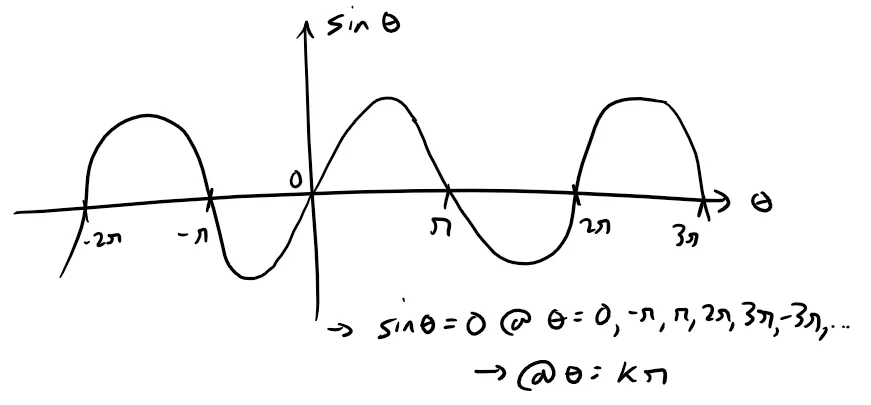
Exercise 2

Let:

Find the intervals of convergence for f, f', and f''.

Solution:

This looks like a series we can apply the Ratio Test to:

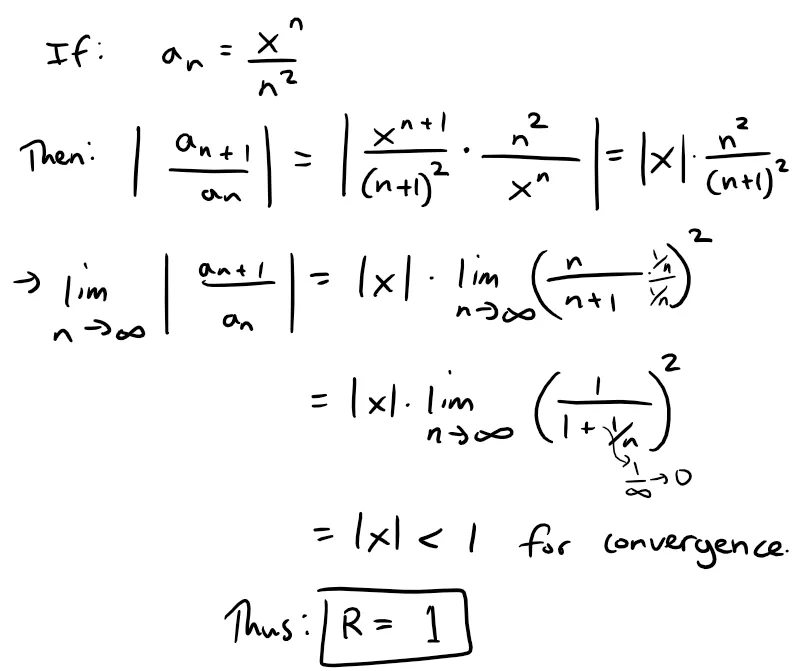
When x = ±1, then:

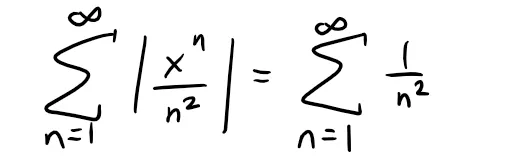
which is a convergent p-series (p = 2 > 1), hence f is absolutely convergent and therefore convergent at x = ±1, so the interval of convergence for f is [-1, 1].

By Theorem 1, the radii of convergence of f' and f'' are both 1, so we need only check the endpoints.

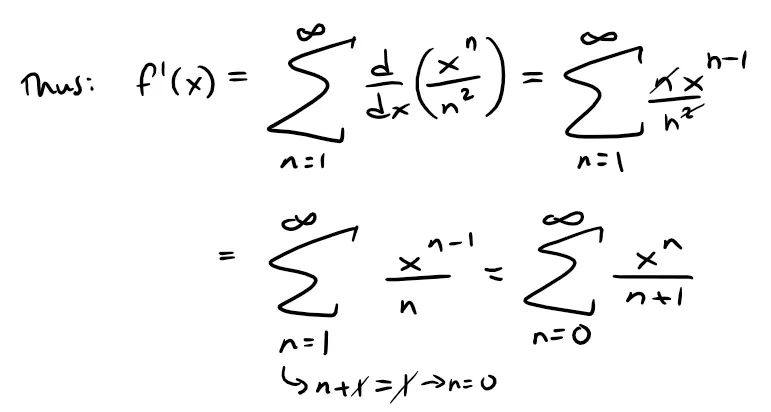
This series diverges for x = 1 (harmonic p = 1 series) and converges for x = -1 via the Alternating Series Test; which I covered in Example 1 in my earlier video.

@mes/infinite-sequences-and-series-alternating-tests

Thus the interval of convergence for f' is [-1, 1).

For the second derivative, we have:

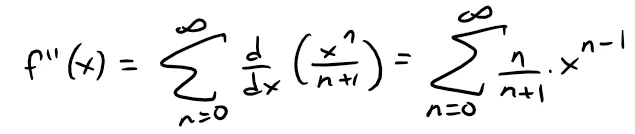
Recall the Test for Divergence from my earlier video:

@mes/infinite-series-definition-examples-geometric-series-harmonics-series-telescoping-sum-more

Thus, we have:

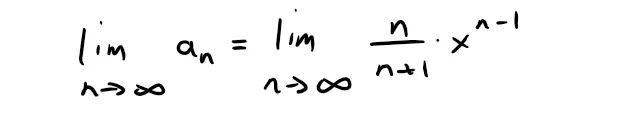
Since at x = ±1, the term xn-1 alternates between +1 and -1 thus the Test for Divergence requires that the term n/(n + 1) must approach 0.

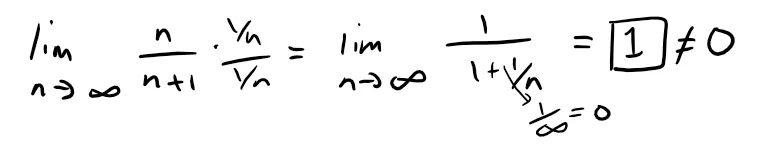
Thus, by the Test for Divergence the second derivative f'' diverges at both 1 and -1, so its interval of convergence is (-1, 1).

Exercise 3: Proof of Theorem 1

Recall Theorem 1 from earlier in this video.

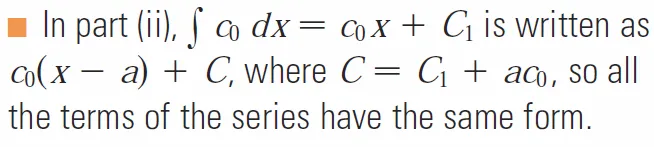
My calculus textbook didn't have the proof for this theorem but I have found one online from the University of Alberta, Canada, website.

http://www.math.ualberta.ca/~isaac/math309/ss17/diff.pdf

Retrieved: 21 December 2019
Archive: https://web.archive.org/web/20191221204509/http://www.math.ualberta.ca/~isaac/math309/ss17/diff.pdf
MES Local PDF Archive: https://1drv.ms/b/s!As32ynv0LoaIh_x2xF7SaAzpxq_x6Q?e=IaBrGC

Theorem 1 Proof:

In this proof we will show that a power series ∑∞n=0 anzn can be differentiated or integrated term by term inside its circle of convergence.

MES Note: This proof involves deriving for the variable z but we can merely replace it with (x - a) to match the theorem used in my calculus book.

First we need the following lemma (intermediate argument).

Lemma:

If:

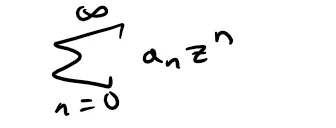
has a radius of convergence R > 0, then:

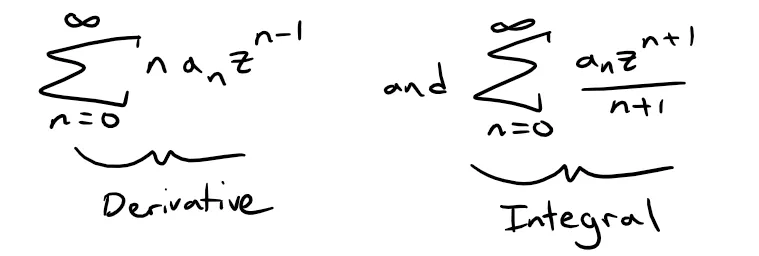
also have a radius of convergence R.

Lemma Derivative Proof:

Let's first look at the derivative part of the lemma.

Let z ϵ C with |z| < R and choose r with |z| < r < R:

MES Note: C is the set of all real and complex numbers; i.e. all numbers. The absolute value of a complex number is just a positive number so it is contained within |z| < R.

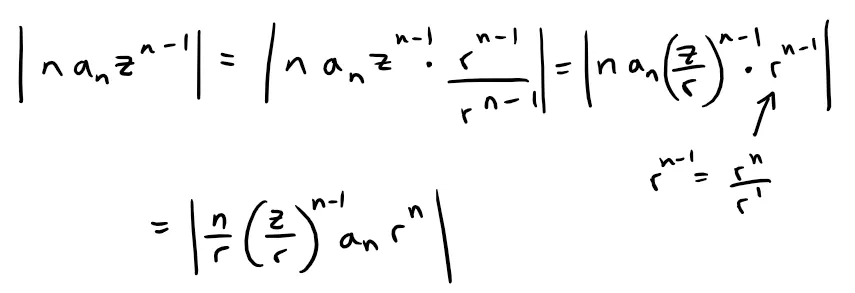
Since r > |z|, then the only terms that can be negative, and hence require the absolute value sign, are z and an; thus:

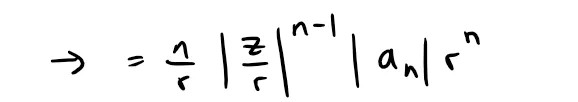
However,

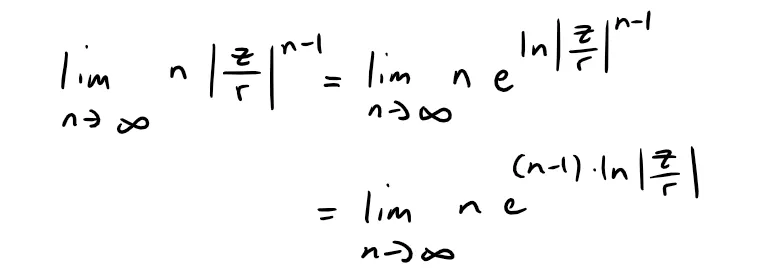
And since |z| < r, then |z/r| = |z|/r < 1, and thus ln|z/r| < 0.

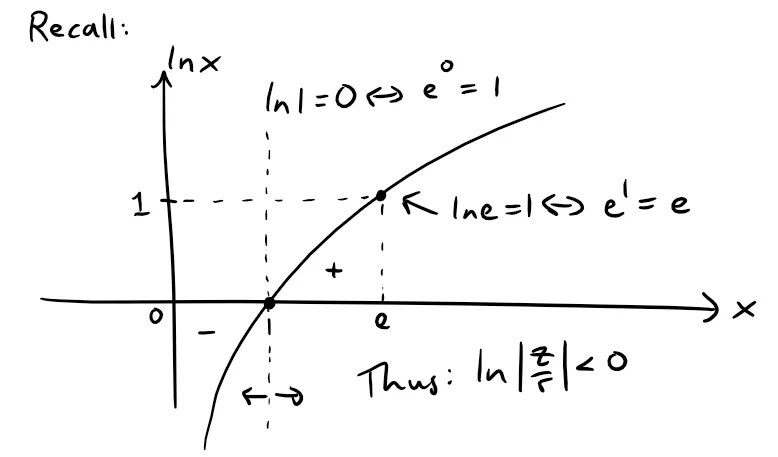
Thus we have:

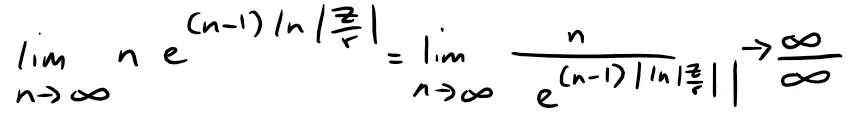
Since this is indeterminate, we can apply L'Hospital's Rule; referenced below.

Retrieved: 23 December 2019
Archive: https://archive.ph/wip/SKgVf

Thus we have:

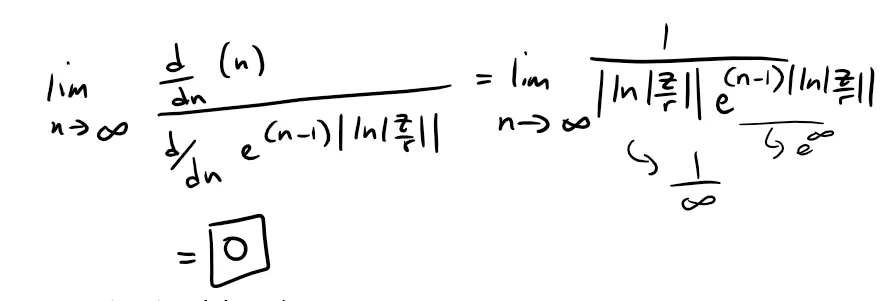
To summarize, since |z| < r, then:

Since this limit is approaching zero, there exists an integer n0 such that for all n ≥ n0:

And thus:

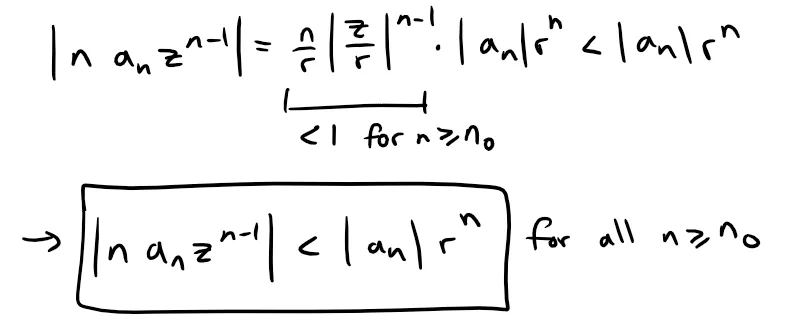
Since we are given that ∑∞n=0 |an|rn converges because r < R, thus by the Comparison Test, ∑∞n=1 nanzn-1 converges absolutely (and hence converges) for all z ϵ C with |z| < R.

Case Where |z| > R

On the other hand, if z ϵ C with |z| > R, we can choose a positive number r such that we have R < r < |z|, and if ∑∞n=1 nanzn-1 converges (from the above derivation), then r < |z| implies that ∑∞n=1 n|an|rn-1 converges.

However,

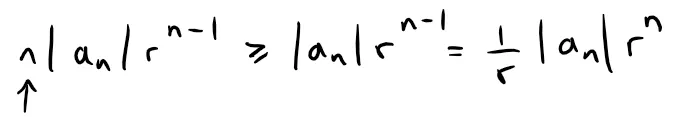
Since 1/r is just a constant, this implies that ∑∞n=0 |an|rn converges, which in turn implies that ∑∞n=0 anrn converges.

This is a contradiction since r > R.

Therefore, ∑∞n=0 nanzn-1 diverges for all z ϵ C with |z| > R.

Thus we have shown that if ∑∞n=0 anzn has a radius of convergence R > 0, then ∑∞n=0 nanzn-1 converges for |z| < R, and diverges for |z| > R, that is, the radius of convergence of this power series is also R.

Lemma Integral Proof:

Now let R' > 0 be the radius of convergence of ∑∞n=0 anzn+1/(n+1), then from the above, the series ∑∞n=0 anzn also has a radius of convergence R', and therefore R' = R.

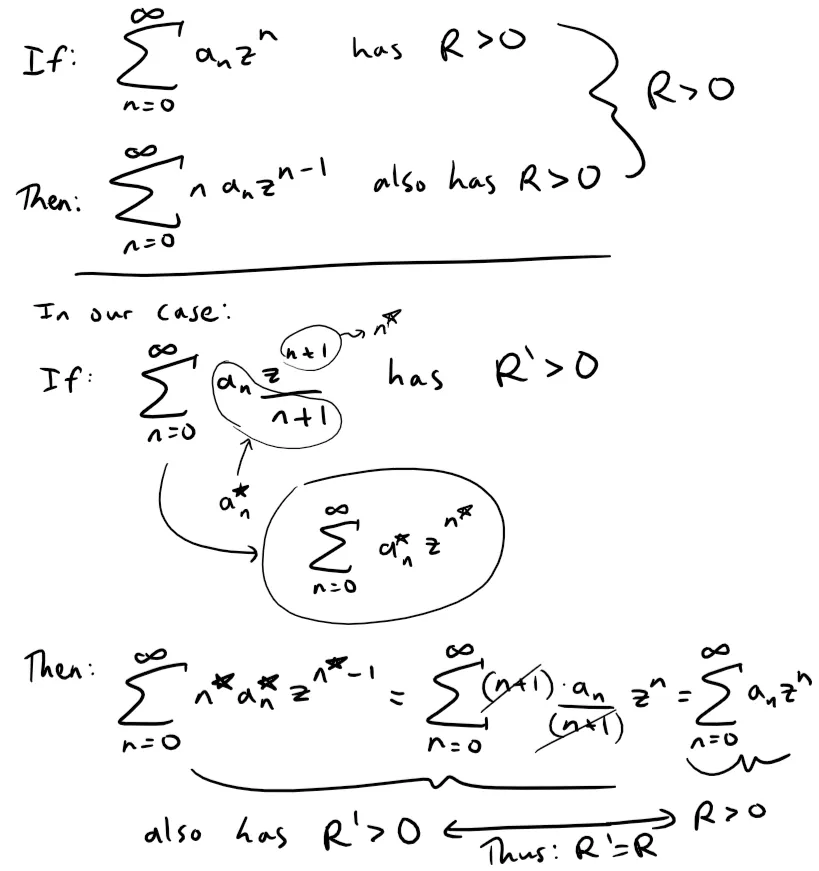
And now the promised result, with nary (or not) a mention of uniform convergence.

Theorem 1 Using z = (x - a)

Note that the theorem the PDF proof uses involves the term z but we can make it in the form shown in my calculus book by merely replacing it with z = (x - a).

Note also that the integral part is from 0 to z which thus is a definite integral and merely results in removing the constant of integration present in the form of this theorem from my calculus book.

Theorem 1a Derivative Proof:

(a) Let z ϵ C with |z| < R, and choose H > 0 so that |z| + H < R (z and H are fixed).

Now let h ϵ C be such that 0 < |h| ≤ H and define:

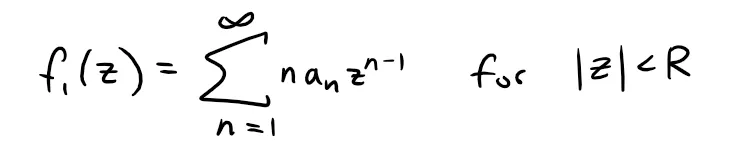
First, recall the definition of a derivative as a function.

Retrieved: 22 December 2019
Archive: https://archive.ph/jVuBK

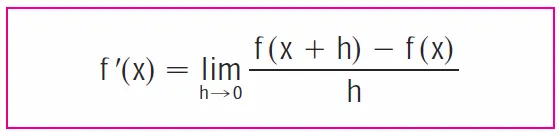
Now, we can do some algebra to get this derivative form:

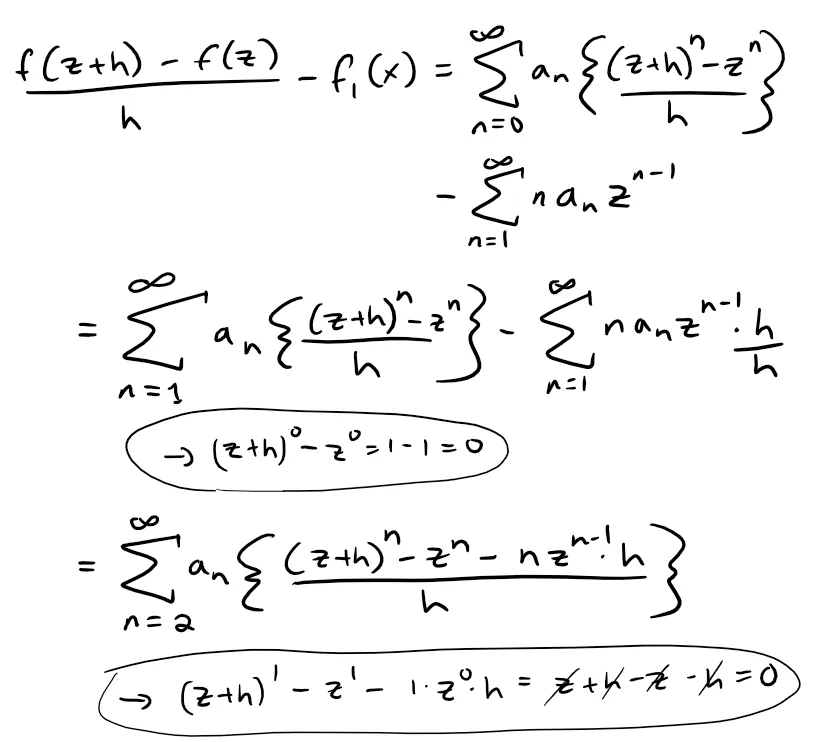
Therefore; and taking the absolute values of both sides, we have:

Brief Overview of the Binomial Theorem

This proof utilizes the Binomial Theorem in Summation Form (hence have two summations) to simplify the (z + h)n term. This theorem is beyond what I have covered so far in my videos, so for now I will just list a brief overview and formulation below.

https://en.wikipedia.org/wiki/Binomial_theorem

Retrieved: 26 December 2019
Archive: https://archive.ph/7hDUV

Binomial theorem

In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the polynomial (x + y)n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with b + c = n, and the coefficient a of each term is a specific positive integer depending on n and b. For example (for n = 4),

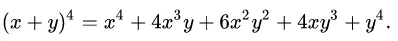
The coefficient a in the term of axbyc is known as the binomial coefficient:

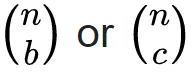
(the two have the same value). These coefficients for varying n and b can be arranged to form Pascal's triangle. These numbers also arise in combinatorics, where (nb) gives the number of different combinations of b elements that can be chosen from an n-element set. Therefore (nb) is often pronounced as "n choose b".

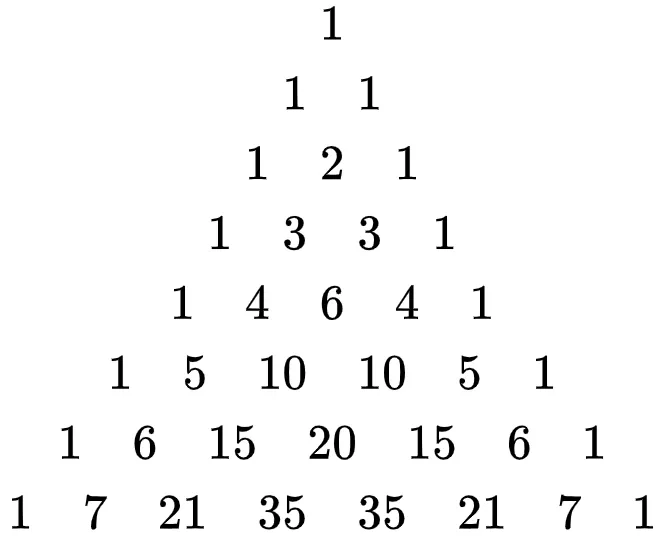
The binomial coefficient (nb) appears as the bth entry in the nth row of Pascal's triangle (counting starts at 0). Each entry is the sum of the two above it.

…

…

…

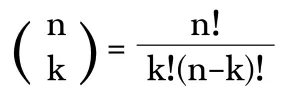
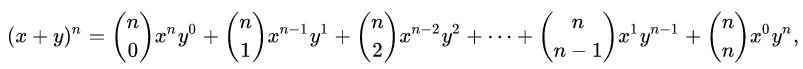
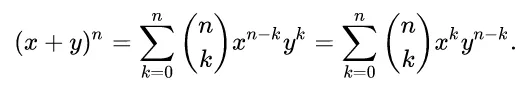
MES Note: Note the symmetry in the formula and terms.

Note also the basic procedure of utilizing double summations:

To simplify our earlier expression, first note the following pattern of the first two terms for any value of n:

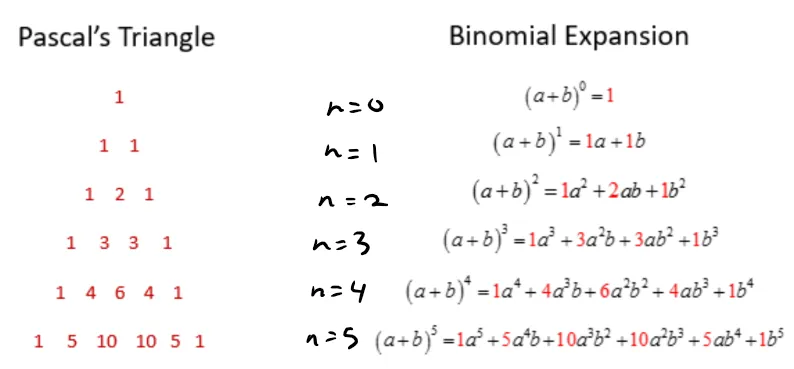
The first two terms are always:

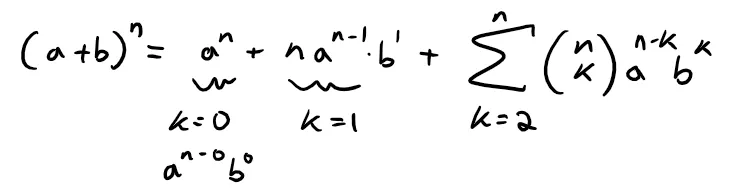
Thus starting from our earlier expression, we can now get to where the PDF proof magically jumps to:

And simplifying further and factoring out a |h| we get:

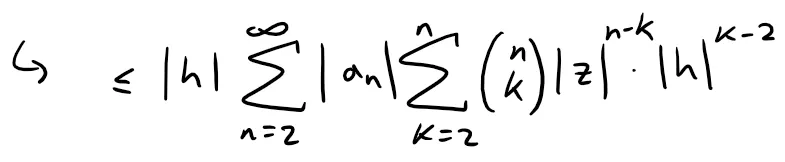
Now recall that we defined h ϵ C be such that 0 < |h| ≤ H, thus we can continue further:

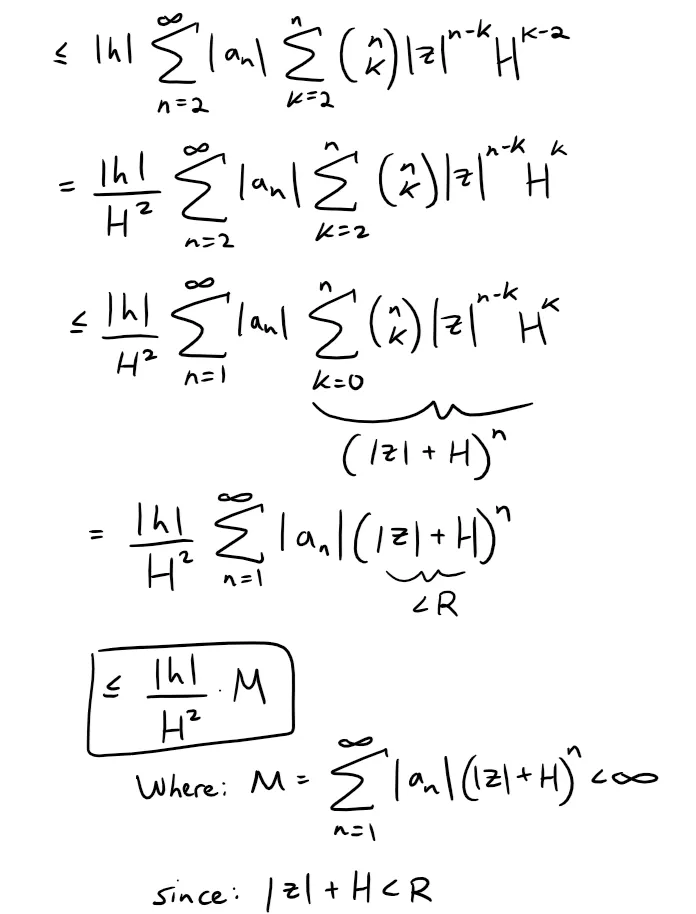
Therefore, we have:

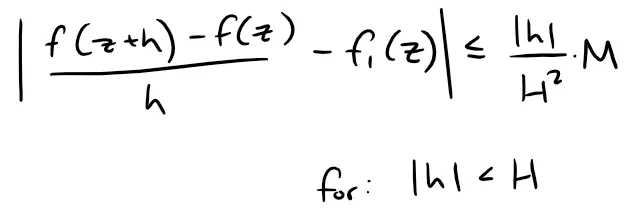
Letting h → 0, then for |z| < R we have:

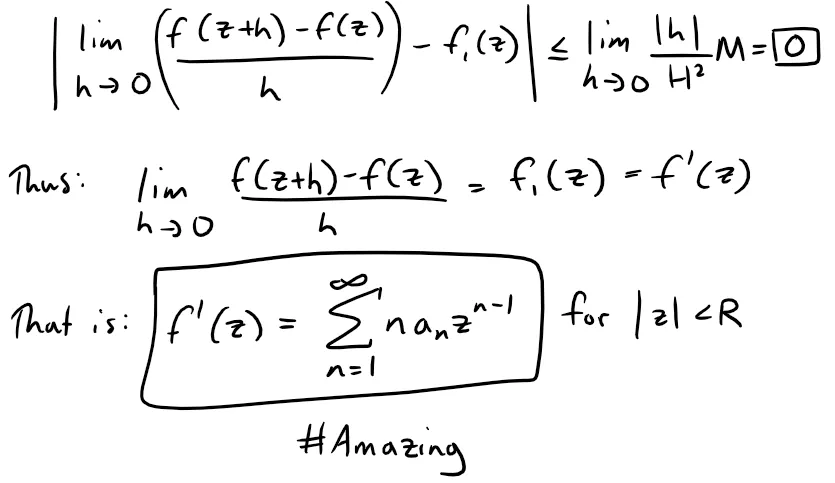
Theorem 1b Integral Proof:

(b) Now let:

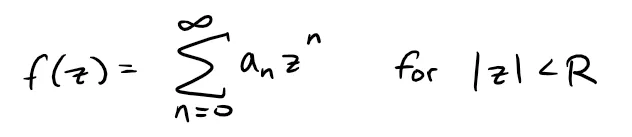
and define:

Then, from part (a), f is a function locally given by a convergent power series and therefore differentiable in the domain |z| < R, and so is continuous there, thus its antiderivative and therefore its integral exists via the Fundamental Theorem of Calculus.

MES Note: A function that is locally given by a convergent power series and therefore differentiable is called an "analytic function".

And this antiderivative of f is just F since F' = f, as per part (a) of this theorem:

Thus F is an antiderivative of f in the domain |z| < R.

Therefore, if |z| < R and P is any contour or path joining 0 and z which lies entirely inside the circle of convergence, then we can take the integral:

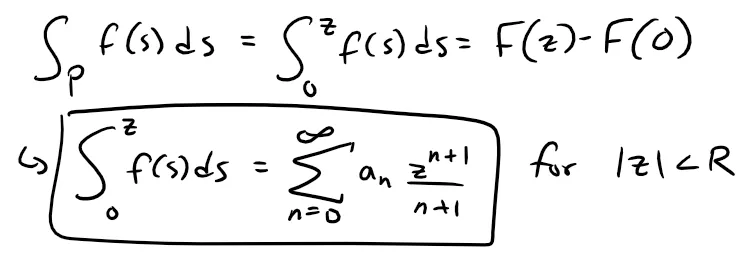
PDF Proof Note:

If the power series:

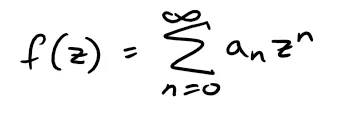
has radius of convergence R > 0, then f'(z) exists for all z with |z| < R, that is, any power series is an analytic function inside its circle of convergence.

mathematics
calculus
science
steemiteducation
steemstem
messcience
mesexperiments
antigravity
mesduality
5 years ago
mes72
via peakd
$ 0.430
40
1
H2
H3
H4
3 columns
2 columns
1 column
Join the conversation now
Logo
Center