Infinite Sequences and Series: Power Series

72
5 years ago
in
#mathematics

In this video I go over further into infinite sequences and series and this time look at the Power Series which is a series in which a power function is being summed up. The power series has many useful applications such as the vibrations of a drum as in the Bessel function and has to do with the particular behavior of the power series to oscillate in large amplitudes initially and dissipate with distance and/or time. I go over many examples, exercises, and proofs in yet another epic long math video, so follow along to learn more!

The topics and their timestamps in the video are listed below:

  1. @ 1:54 - Power Series
    • @ 9:41 - Note on Trigonometric Series and the Fourier Series
    • @ 10:40 - Example 1
    • @ 14:33 – Note on Factorials
    • @ 15:23 - Example 2
  2. @ 24:31 - Note on Bessel Functions
    • @ 25:49 - Example 3: Bessel Function of Order 0
  3. @ 49:41 - Theorem 1
    • @ 55:54 - Summary of Previous Examples
    • @ 58:35 - Example 4
    • @ 1:07:22 - Example 5
  4. Exercises
    • @ 1:17:18 - Exercise 1: Bessel Function of Order 1
    • @ 1:34:44 - Exercise 2: Proof of Theorem 1
      • @ 1:35:53 - Theorem 2
      • @ 1:49:24 - Theorem 3
      • @ 1:53:48 - Completeness Axiom

Watch Video On:

Download Video Notes: https://1drv.ms/b/s!As32ynv0LoaIh_ZL0WExNvIL4J0s2Q?e=GkZR2u

View Video Notes Below!

Download These Notes: Link is in Video Description.
View These Notes as an Article: @mes
Subscribe via Email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donate

Reuse of My Videos:

  • Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.

Fight Back Against Censorship:

  • Bookmark sites/channels/accounts and check periodically
  • Remember to always archive website pages in case they get deleted/changed.

Join my private Discord Chat Room: https://mes.fm/chatroom

Check out my Reddit and Voat Math Forums:

Buy "Where Did The Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
Follow My #FreeEnergy Video Series: https://mes.fm/freeenergy-playlist
Watch my #AntiGravity Video Series: @mes/series

  • See Part 6 for my Self Appointed PhD and #MESDuality Breakthrough Concept!

Follow My #MESExperiments Video Series: @mes/list

NOTE #1: If you don't have time to watch this whole video:

NOTE #2: If video volume is too low at any part of the video:

Infinite Sequences and Series: Power Series

Power Series.jpeg

Calculus Book Reference

Note that I mainly follow along the following calculus book:

  • Calculus: Early Transcendentals Sixth Edition by James Stewart

Topics to Cover

    • Power Series
    • Note on Trigonometric Series and the Fourier Series
    • Example 1
    • Note on Factorials.
    • Example 2
  2. Note on Bessel Functions
    • Example 3: Bessel Function of Order 0
  3. Theorem 1
    • Summary of Previous Examples
    • Example 4
    • Example 5
  4. Exercises
    • Exercise 1: Bessel Function of Order 1
    • Exercise 2: Proof of Theorem 1
      • Theorem 2
      • Theorem 3
      • Completeness Axiom

Power Series

A power series is a series of the form:

where x is a variable and the cn's are constants called the coefficients of the series.

For each fixed x, the power series is as series of constants that we can test for convergence or divergence.

A power series may converge for some values of x and diverge for other values of x.

The sum of the series is a function:

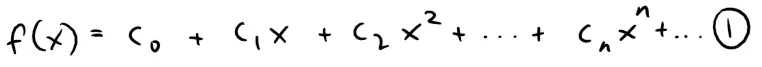
whose domain is the set of all x for which the series converges.

Notice that f resembles a polynomial.

The only difference is that f has infinitely many terms.

For instance, if we take cn = 1 for all n, the power series becomes the geometric series:

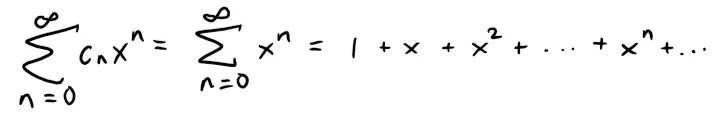
which converges when -1 < x < 1 and diverges when |x| ≥ 1.

Recall the geometric series and an earlier example covering this power series in my earlier video.

@mes/infinite-series-definition-examples-geometric-series-harmonics-series-telescoping-sum-more

Retrieved: 27 July 2019
Archive: http://archive.fo/FGAyJ

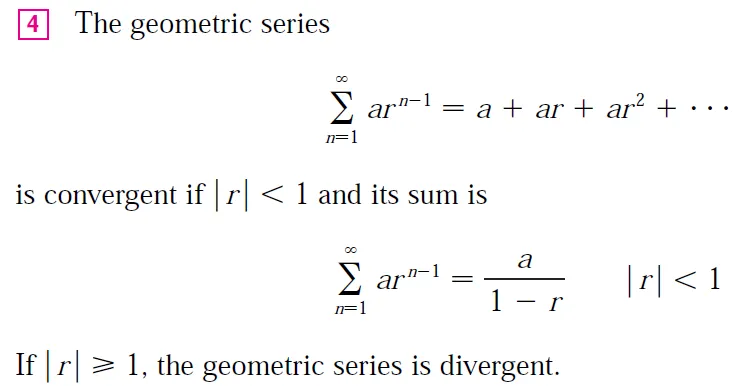
More generally, a series of the form:

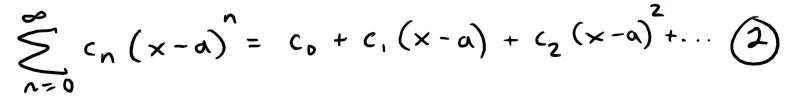
is called a power series in (x - a) or a power series centered at a or a power series about a.

Notice that in writing out the term corresponding to n = 0 in Equations 1 and 2 we have adopted the convention that (x - a)0 = 1 even when x = a.

Notice also that when x = a, all of the terms are 0 for n ≥ 1 and so the power series in Equation 2 always converges when x = a.

Note on Trigonometric Series

A power series is a series in which each term is a power function.

A trigonometric series:

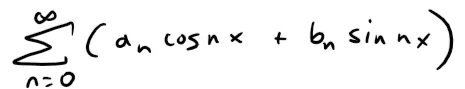
is a series whose terms are trigonometric functions.

The trigonometric series is the basis behind the famous Fourier series and which I will be covering in future videos.

Example 1

For what values of x is the following series convergent?

Solution:

We use the Ratio Test from my earlier video:

@mes/infinite-sequences-and-series-absolute-convergence-and-the-ratio-root-tests

Retrieved: 17 September 2019
Archive: http://archive.fo/ANfgj

We let an, as usual, denote the n-th term of the series, then an = n! xn.

If x ≠ 0, we have:

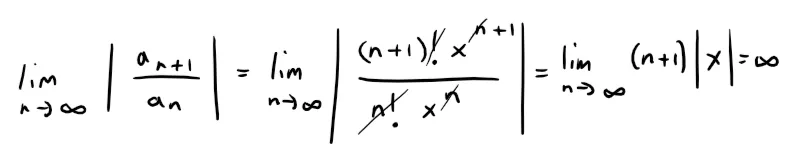
By the Ratio Test, the series diverges when x ≠ 0.

Thus the given series converges only when x = 0.

Note on Factorials

Notice that:

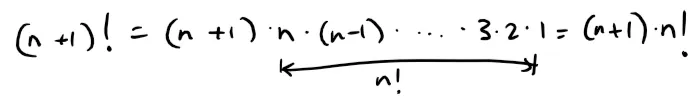
Example 2

For what values of x does the following series converge?

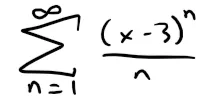
Solution:

Let an = (x - 3)n/n. Then:

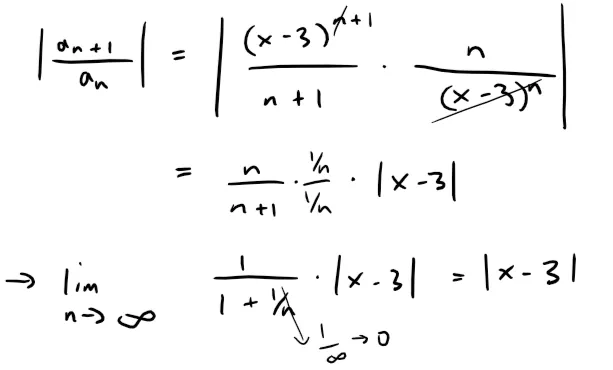
By the Ratio Test, the given series is absolutely convergent, and therefore convergent, when |x - 3| < 1 and divergent when |x - 3| > 1.

Now:

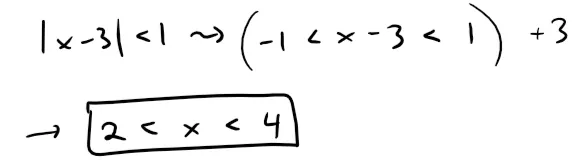
So the series converges when 2 < x < 4 and diverges when x < 2 or x > 4.

The Ratio Test gives no information when |x - 3| = 1 so we must consider x = 2 and x = 4 separately.

If we put x = 4 in the series, it becomes ∑ 1/n , the harmonic series (i.e. p-series of p = 1), which is divergent.

@mes/infinite-sequences-and-series-the-integral-test-and-estimate-of-sums

Retrieved: 26 August 2019
Archive: http://archive.fo/vapHa

If x = 2, the series ∑ (-1)n/n, which converges by the Alternating Series Test which I covered in my earlier video.

@mes/infinite-sequences-and-series-alternating-tests

Retrieved: 26 August 2019
Archive: http://archive.fo/9neM8

Thus the given power series converges for 2 ≤ x < 4.

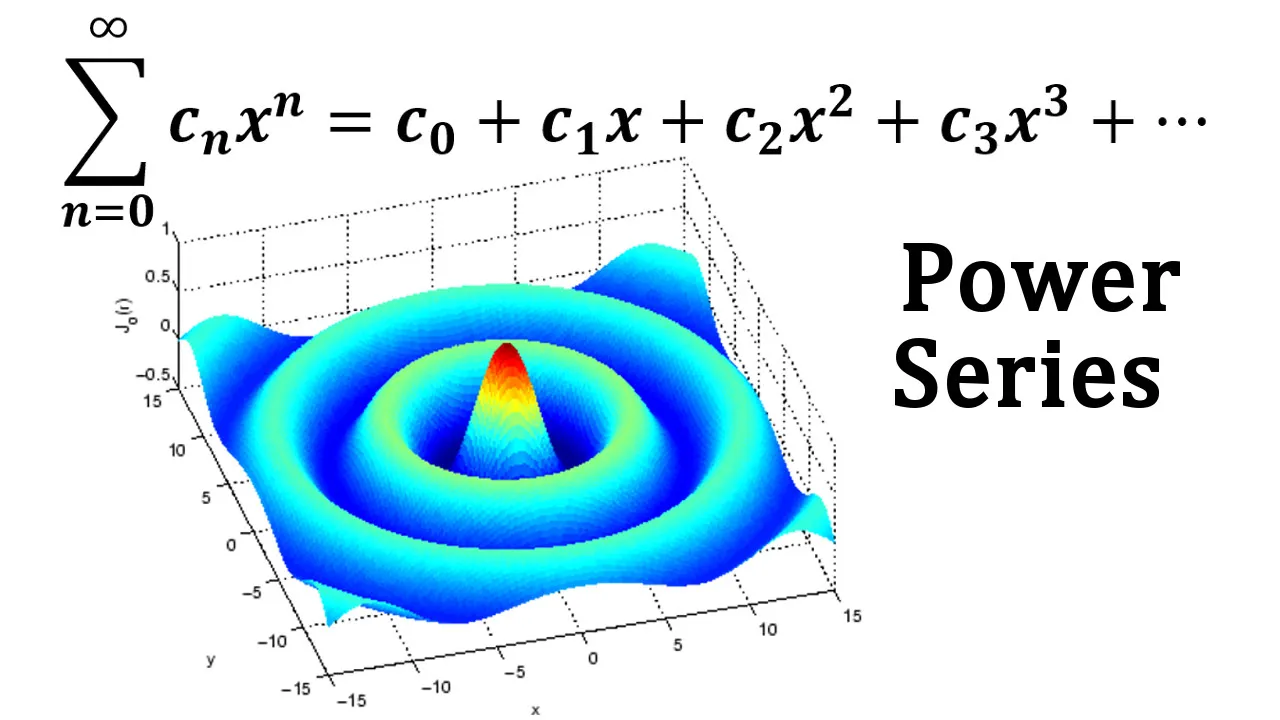
Note on Bessel Functions

We will see that the main use of a power series is that it provides a way to represent some of the most important functions that arise in mathematics, physics, and chemistry.

In particular, the sum of the power series in the next example is called a Bessel function, after the German astronomer Friedrich Bessel (1784 - 1846), and the function given in Exercise 1 later in this video is another example of a Bessel function.

In fact, these functions first arose when Bessel solved Kepler's equation for describing planetary motion.

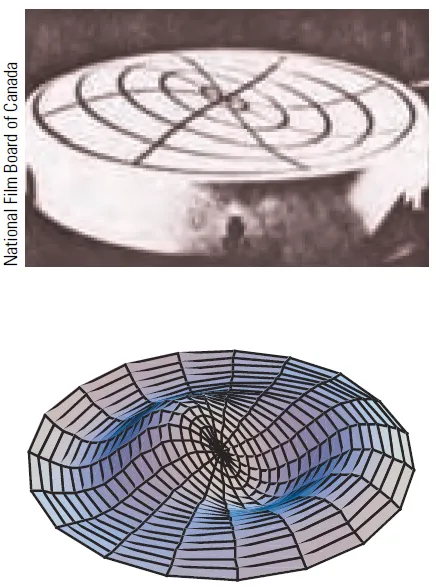
Since that time, these functions have been applied in many different physical situations, including the temperature distribution in a circular plate and the shape of a vibrating drumhead.

Notice how closely the following computer-generated model (which involves Bessel functions and cosine functions) matches the photograph of a vibrating rubber membrane.

#Amazing

Example 3: Bessel Function of Order 0

Find the domain of the Bessel function of order 0 defined by:

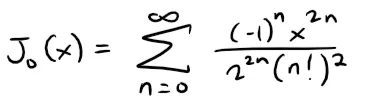
Solution:

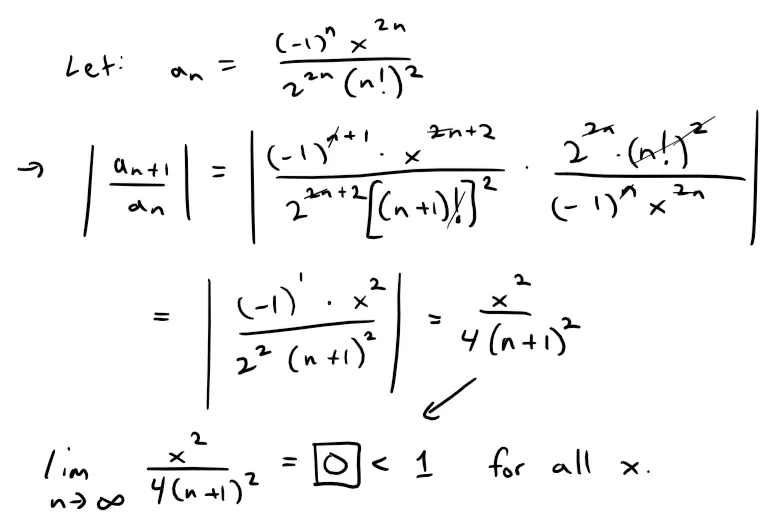
Thus, by the Ratio Test, the given series converges for all values of x.

In other words, the domain of the Bessel function J0 is (-∞ , ∞) = R (i.e. all real numbers).

Recall that the sum of a series is equal to the limit of the sequence of partial sums.

So when we define the Bessel function in Example 3 as the sum of a series we mean that, for every real number x,

The first few partial sums are:

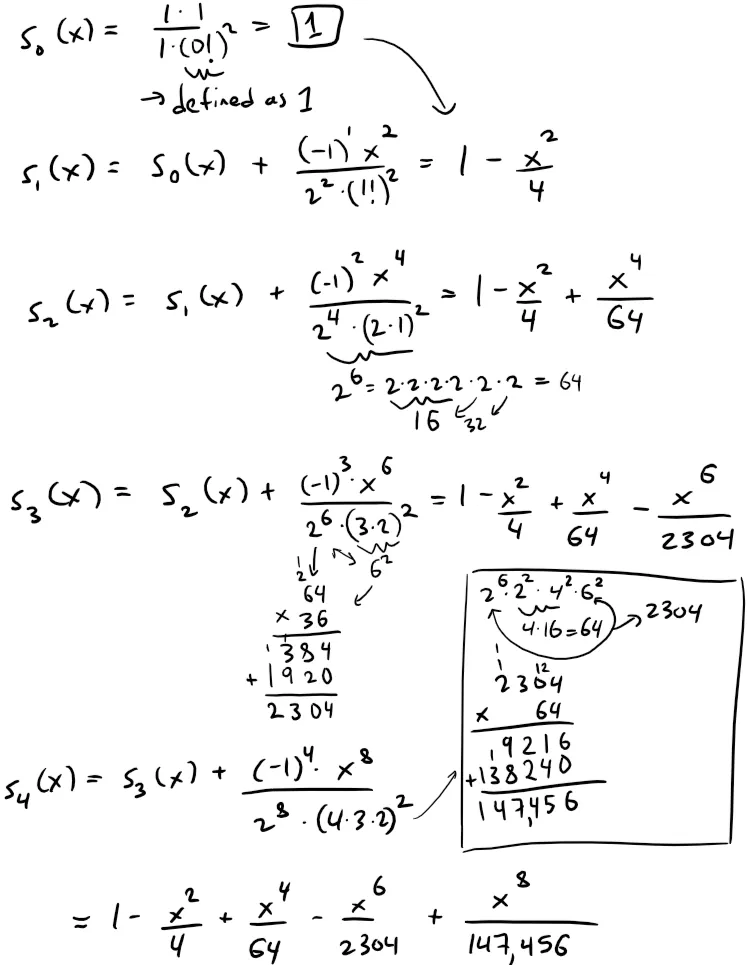
Calculations Check:

  • 24·(2·1)2 = 64
  • 26·(3·2·1)2 = 2,304
  • 28·(4·3·2·1)2 = 147,456

The following figure shows the graphs of these partial sums, which are polynomials.

https://www.desmos.com/calculator/xpvthh1pca

Retrieved: 23 September 2019
Archive: Not Available

Partial sums of the Bessel function J0

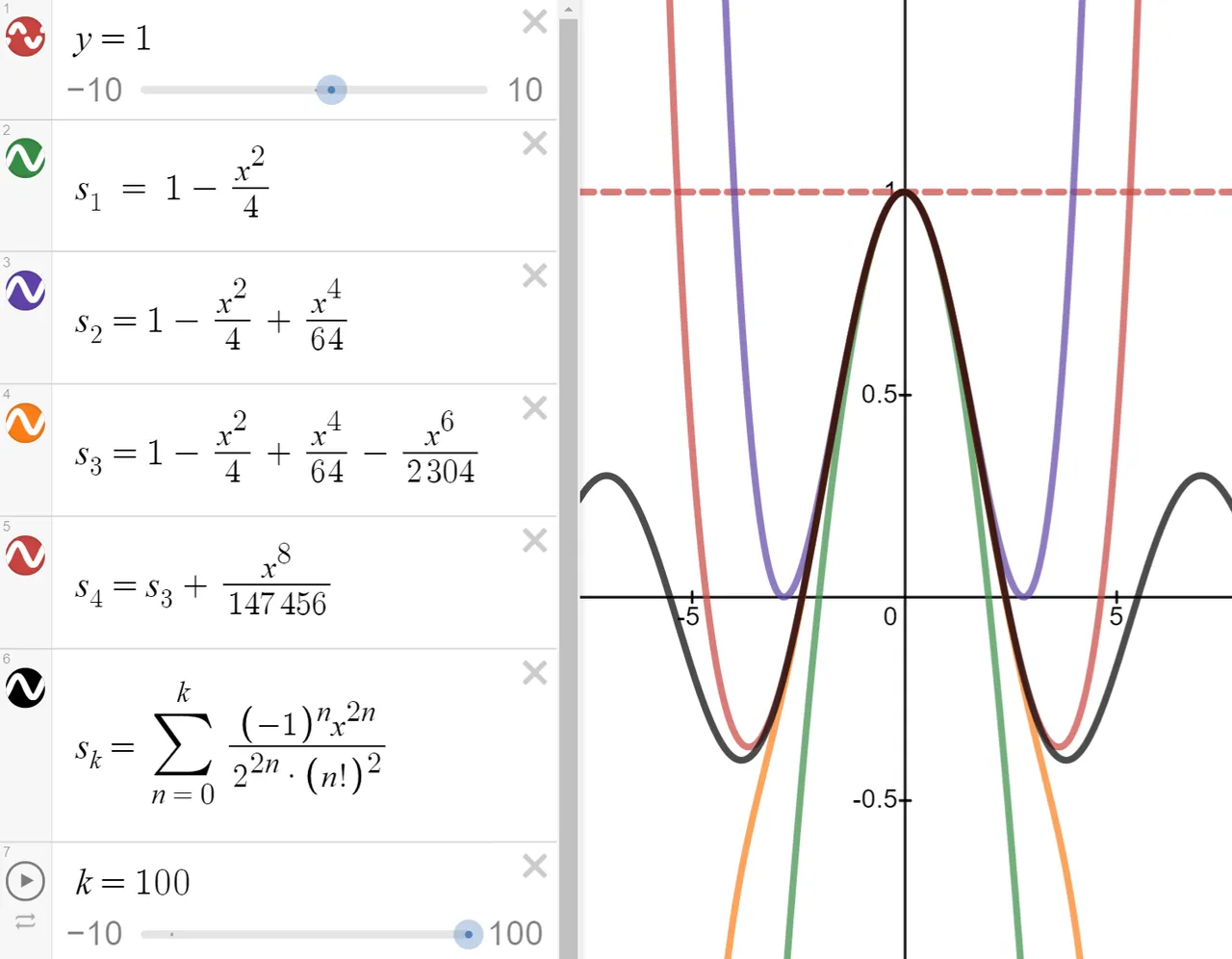
They are all approximations to the function J0, but notice that the approximations become better when more terms are included.

The following figure shows a more complete graph of the Bessel function.

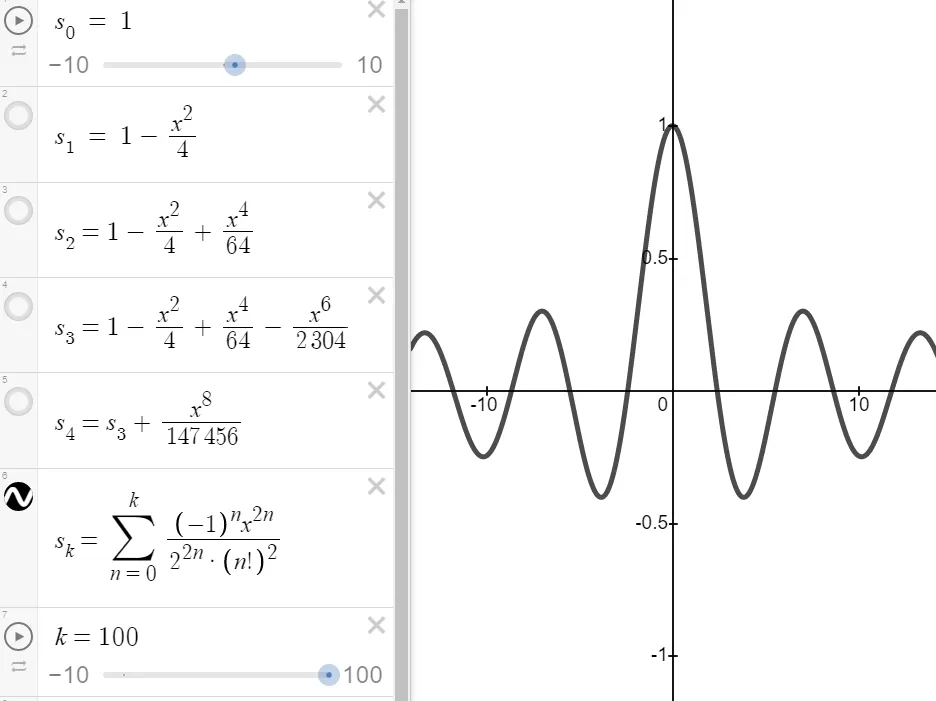
For the power series that we have looked at so far, the set of values of x for which the series is convergent has always turned out to be an interval [a finite interval for the geometric series and the series in Example 2, the infinite interval (-∞ , ∞) in Example 3, and a collapsed interval [0 , 0] = {0} in Example 1].

The following theorem, proved in Exercise 2 later in this video, says that this is true in general.

Theorem 1

For a given power series ∑∞n=0 cn(x - a)n, there are only three possibilities:

(i) The series converges only when x = a.

(ii) The series converges for all x.

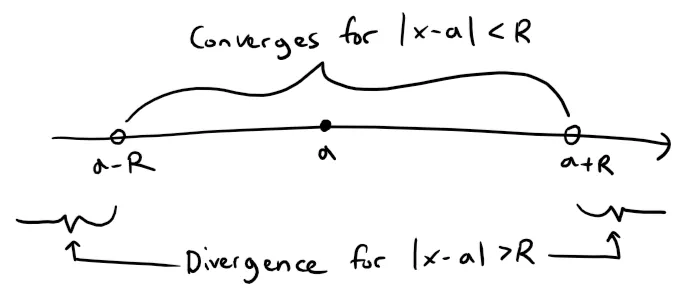
(iii) There is a positive number R such that the series converges if |x - a| < R and diverges if |x - a| > R.

The number R in case (iii) is called the radius of convergence of the power series.

By convention, the radius of convergence is R = 0 in case (i) and R = ∞ in case (ii).

The interval of convergence of a power series is the interval that consists of all values of x for which the series converges.

In case (i) the interval consists of just a single point a.

In case (ii) the interval is (-∞ , ∞).

In case (iii) note that the inequality |x - a| < R can be rewritten as a - R < x < a + R.

When x is an endpoint of the interval, that is, x = a ± R, anything can happen - the series might converge at one or both endpoints or it might diverge at both endpoints.

Thus in case (iii) there are four possibilities for the interval of convergence:

The situation is illustrated in the figure below:

Summary of Previous Examples

We summarize here the radius and interval of convergence for each of the examples already considered in this section.

In general, the Ratio Test (or sometimes the Root Test) should be used to determine the radius of convergence R.

The Ratio and Roots Tests always fail when x is an endpoint of the interval of convergence, so the endpoints must be checked with some other test.

Example 4

Find the radius of convergence and interval of convergence of the series:

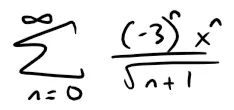
Solution:

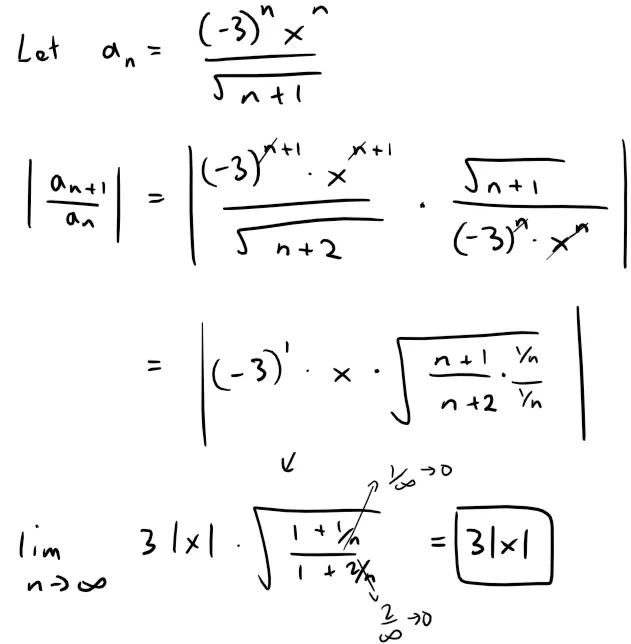
By the Ratio Test, the given series converges if 3|x| < 1 and diverges if 3|x| > 1.

Thus it converges if |x| < 1/3 and diverges if |x| > 1/3.

This means that the radius of convergence R = 1/3.

We know the series converges in the interval (-1/3 , 1/3), but we must now test for convergence at the endpoints of this interval.

If x = -1/3, the series becomes:

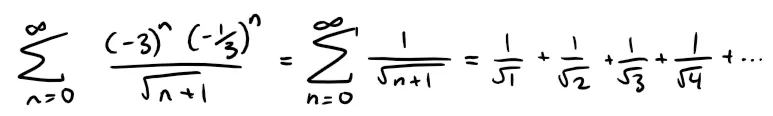
which diverges (Using the Integral Test or simply observe that it is a p-series with p = 1/2 < 1.)

If x = 1/3, the series is:

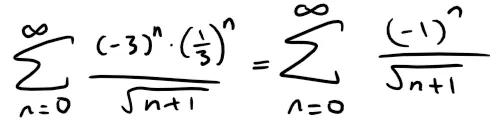
which converges by the Alternating Series Test.

Therefore the given power series converges when -1/3 < x ≤ 1/3, so the interval of convergence is (-1/3 , 1/3].

Example 5

Find the radius of convergence and interval of convergence of the series:

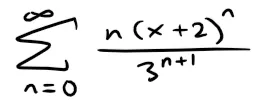
Solution:

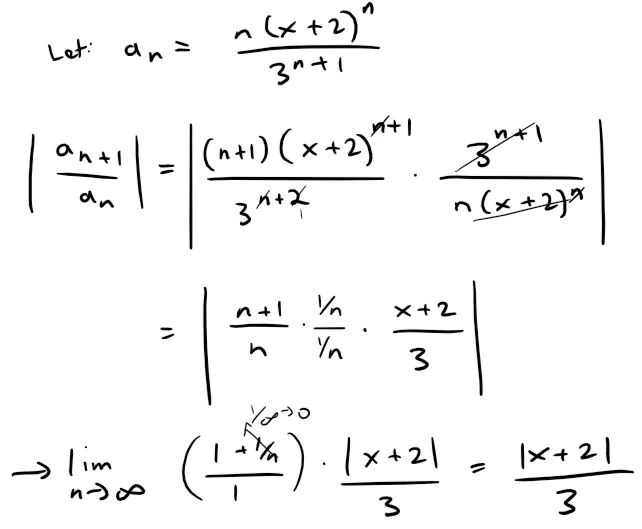
By the Ratio Test, the series converges if |x + 2|/3 < 1 and it diverges if |x + 2|/3 > 1.

So it converges if |x + 2| < 3 and diverges if |x + 2| > 3.

Thus the radius of convergence is R = 3.

The inequality |x + 2| < 3 can be written as -5 < x < 1, so we test the series at the endpoints -5 and 1.

When x = -5, the series is:

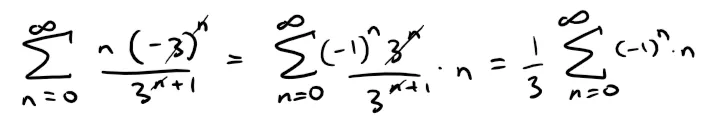
which diverges by the Test for Divergence [(-1)nn doesn't converge to 0].

@mes/infinite-series-definition-examples-geometric-series-harmonics-series-telescoping-sum-more

Retrieved: 27 July 2019
Archive: http://archive.fo/FGAyJ

When x = 1, the series is:

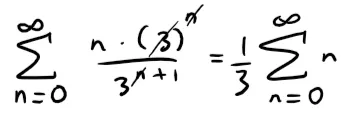
which also diverges by the Test for Divergence.

Thus the series converges only when - 5 < x < 1, so the interval of convergence is (-5 , 1).

Exercises

Exercise 1: Bessel Function of Order 1

The function J1 defined by:

is called the Bessel function of order 1.

Note: Compare with J0 in Example 3:

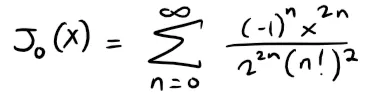
(a) Find its domain.

(b) Graph the first several partial sums on a common screen.

(c) If your CAS has built-in Bessel functions, graph J1 on the same screen as the partial sums in part (b) and observe how the partial sums approximate J1.

Solution:

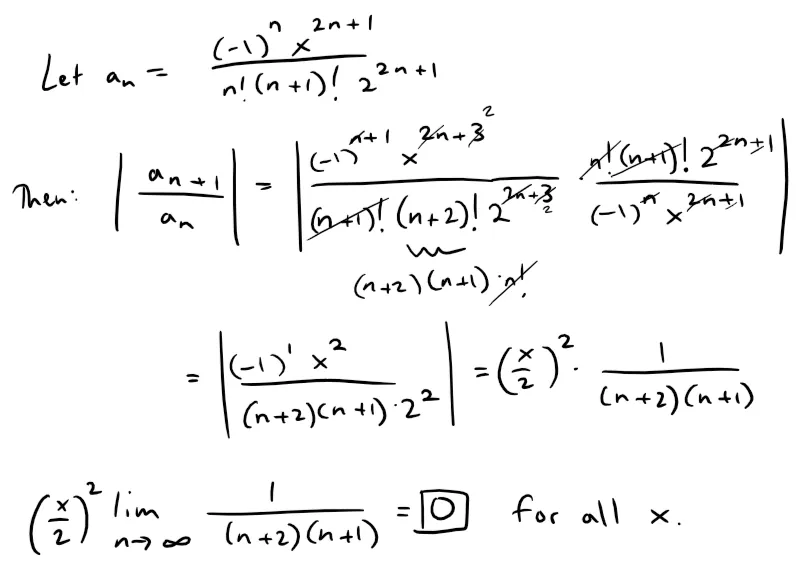
So J1(x) converges for all x and its domain is (-∞ , ∞).

(b) The initial terms of J1(x) up to n = 5 are:

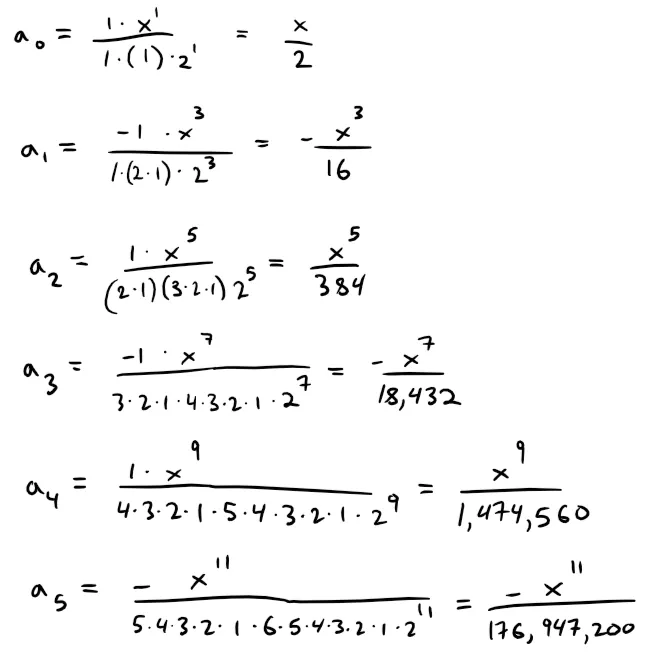
Calculations Check:

  • 2·2^3 = 16
  • 2·3·2·2^5 = 384
  • 3·2·4·3·2·2^7 = 18,432
  • 4·3·2·5·4·3·2·2^9 = 1,474,560
  • 5·4·3·2·6·5·4·3·2·2^11 = 176,947,200

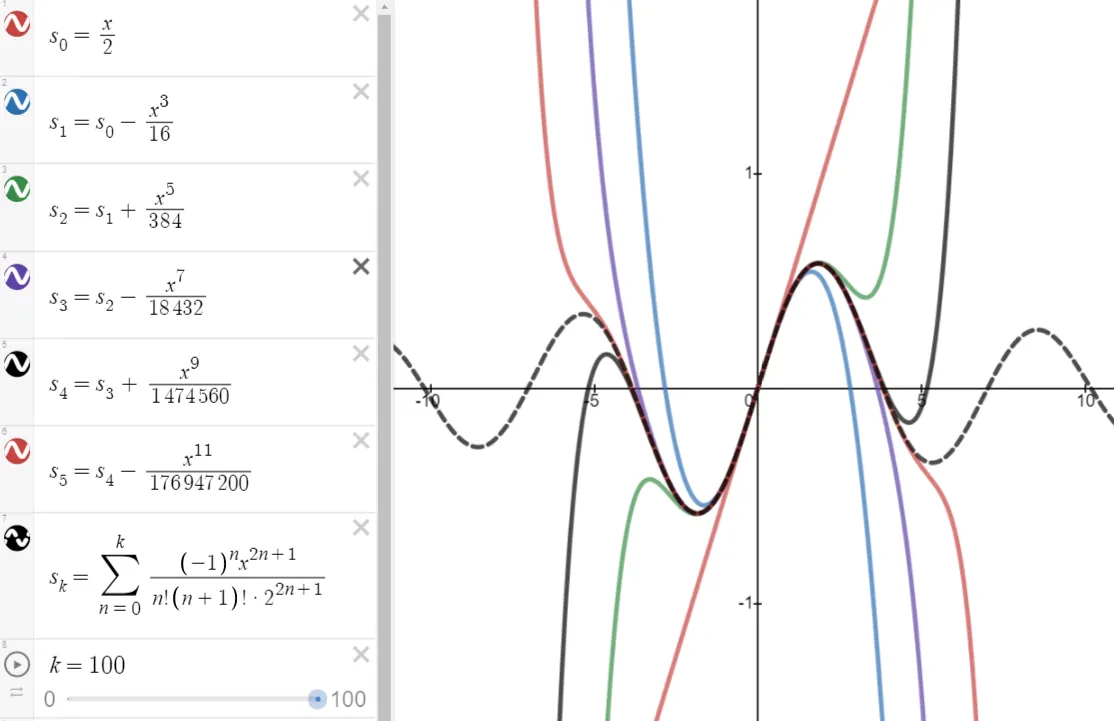
The partial sums are graphed in the following figure:

https://www.desmos.com/calculator/soaqt1sqnc

Retrieved: 22 September 2019
Archive: Not Available

(c) The partial sums seem to approximate J1(x) well near the origin, but as |x| increases, we need to take a large number of terms to get a good approximation.

Exercise 2: Proof of Theorem 1

Prove Theorem 1:

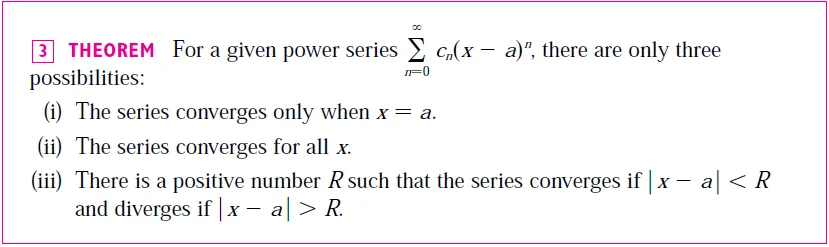
Solution:

In order to prove Theorem 1, we first need the following results from another theorem,
Theorem 2:

Theorem 2

(1) If a power series ∑ cnxn converges when x = b (where b ≠ 0), then it converges whenever |x| < |b|.

(2) If a power series ∑ cnxn diverges when x = d (where d ≠ 0), then it diverges whenever |x| > |d|.

Proof of (1)

Suppose that ∑ cnbn converges.

Then by the Theorem 1 of my earlier video, shown below, we have: limn→∞ cnbn = 0.

@mes/infinite-series-definition-examples-geometric-series-harmonics-series-telescoping-sum-more

Retrieved: 27 July 2019
Archive: http://archive.fo/FGAyJ

Now recall the definition of the limit of a sequence from my earlier video:

@mes/infinite-sequences-limits-squeeze-theorem-fibonacci-sequence-and-golden-ratio-more

Retrieved: 18 June 2019
Archive: http://archive.fo/p1No3

Thus, according to this definition, and with ε = 1, there is a positive integer N such that:

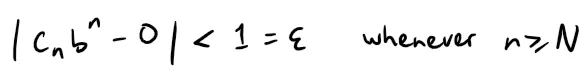
Thus, for n ≥ N, we have:

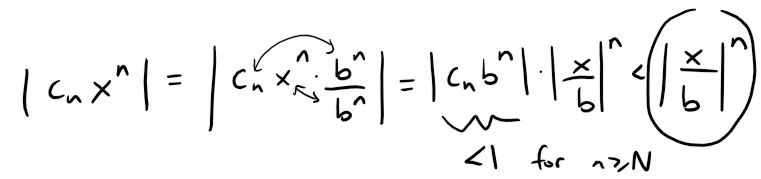
If |x| < |b|, then |x/b| < 1, so ∑ |x/b|n is a convergent geometric series (i.e. |r| < 1).

Therefore, by the Comparison Test (from my earlier video and shown below), the series ∑∞n=N |cnxn| is convergent.

@mes/infinite-sequences-and-series-the-comparison-tests

Retrieved: 26 August 2019
Archive: http://archive.fo/f0SM5

Thus the series ∑ cnxn is absolutely convergent and therefore convergent.

@mes/infinite-sequences-and-series-absolute-convergence-and-the-ratio-root-tests

Proof of (2)

Suppose that ∑ cndn diverges.

If x is any number such that |x| > |d|, then ∑ cnxn cannot converge because, by part (1), the convergence of ∑ cnxn would imply the convergence of ∑ cndn.

Therefore ∑ cnxn diverges whenever |x| > |d|.

Furthermore, we need help from another simpler version of Theorem 1, which we call Theorem 3:

Theorem 3

For a power series ∑ cnxn there are only three possibilities:

(1) The series converges only when x = 0.

(2) The series converges for all x.

(3) There is a positive number R such that the series converges if |x| < R and diverges if |x| > R.

Proof

Suppose that neither case (1) nor case (2) are true.

Then there are nonzero numbers b and d such ∑ cnxn converges for x = b and diverges for x = d.

Therefore the set S = {x | ∑ cnxn converges} is not empty.

By the preceding Theorem 2, the series diverges if |x| > |d|, so |x| ≤ |d| for all x ∈ S.

This says that that |d| is an upper bound for the set S.

Thus, by the Completeness Axiom from my earlier video (and shown below), S has a least upper bound R.

@mes/infinite-sequences-limits-squeeze-theorem-fibonacci-sequence-and-golden-ratio-more

Thus, for our case (and for my understanding) I consider |x| ≤ |d| as being the general upper bound while the "least upper bound" |x| ≤ |R| as the actual upper bound, while R ≤ |d|.

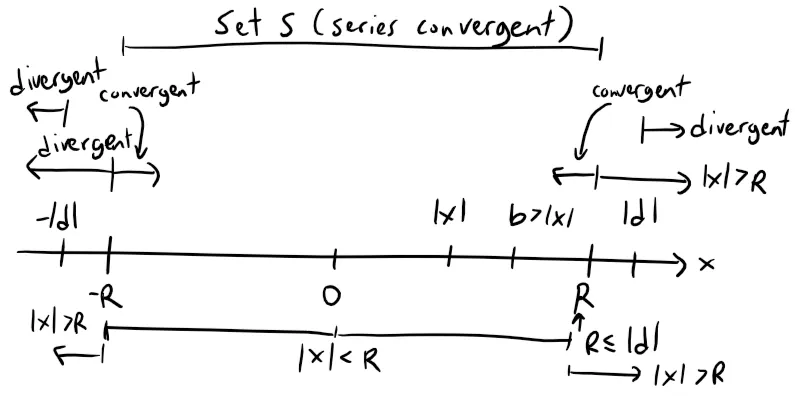
If |x| > R, then x ∉ S, so ∑ cnxn diverges.

If |x| < R, then |x| is not an upper bound for S and so there exists b ∈ S such that b > |x|.

Since b is an element of S, ∑ cnbn converges, thus so too does ∑ cnxn converge by the preceding Theorem 2.

Proof of Theorem 1

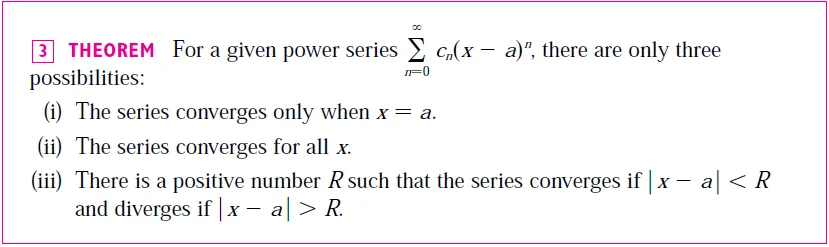
If we make the change of variable u = x - a, then the power series becomes ∑ cnun and we can apply the preceding Theorem 3 to this series.

In case (3) we have convergence for |u| < R and divergence for |u| > R.

Thus we have convergence for |x - a| < R and divergence for |x - a| > R.

mathematics
calculus
science
steemiteducation
steemstem
freeenergy
antigravity
mesduality
mesexperiments
5 years ago
mes72
via peakd
$ 0.474
14
H2
H3
H4
3 columns
2 columns
1 column
Join the conversation now
Logo
Center