
En el artículo anterior, introduje elementos básicos del sistema de interés simple, es decir, del sistema según el cual los intereses no se capitalizan: siempre se calculan sobre el capital inicial. En contraste, el sistema de interés compuesto que presentaré en este artículo fue considerado por Einstein como la “fuerza más poderosa de la naturaleza”, porque los intereses se suman al capital al final de cada período de composición. De nuevo, con apego a la característica fundamental de esta serie, la intención es que cada tema se presente en un artículo estructurado en la forma de guía de estudio para que el lector pueda referirse a ellos cuando lo desee, aprender y refrescar conocimientos. Si algo no se recuerda, sugiero ir a los artículos anteriores de la secuencia.
¿Qué pasaría si los intereses obtenidos o pagados en cada período se sumaran al capital para que en el período siguiente los nuevos intereses se calcularan sobre el total acumulado? Este modelo permite que los intereses se agreguen al capital periódicamente, es decir, permite que se capitalicen. Así, en el período siguiente, el monto que devengará nuevos intereses estará constituido por el monto invertido más los intereses obtenidos hasta ese momento.
Ejemplo hipotético 2.1
Asume que inviertes 1.000 USD en un instrumento financiero que promete devolverte el dinero en cuatro meses (4) y depositar en tu cuenta un interés compuesto del 3% cada mes que transcurra. ¿Qué cantidad tendrás al cabo de los cuatro meses?


Más adelante, aclararé qué tasa de interés (i) es la que se debe introducir en la fórmula para obtener resultados correctos.
Sustituyamos los valores del Ejemplo hipotético 2.1 en la ecuación 2.1:

Lo cual confirma nuestro resultado anterior.
Ejemplo hipotético 2.2
¿Cuántos años deberías mantener una inversión de 1.000 USD en un instrumento financiero que promete pagar un interés compuesto del 8% anual para que tu capital se duplique?
La solución del problema pasa por despejar la variable tiempo (n) de la ecuación 2.1:
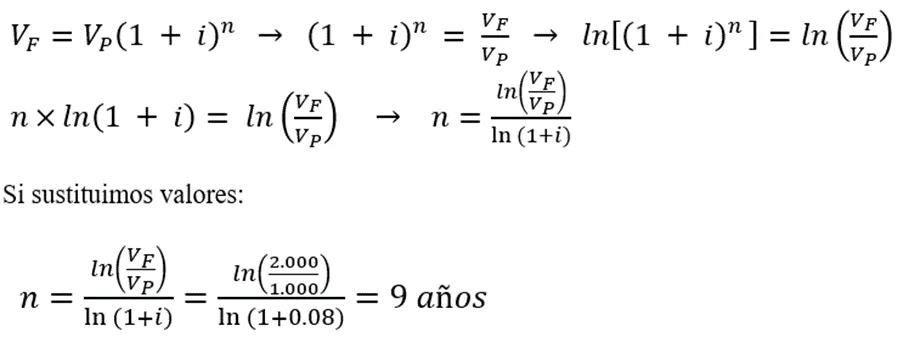
Con un esquema de interés compuesto, ¡el tiempo necesario para que tu capital pase de 1.000 USD a 2.000 USD se reduce a 9 años! En otras palabras, la velocidad de crecimiento de tu dinero aumenta con el interés compuesto (si se compara este resultado con el del ejemplo 1.2 del artículo anterior).
Tipos de tasas de interés compuesto
Para propósitos de esta serie, nos apegaremos a las definiciones que sugieren Blank y Tarquin (2006).
1) Tasa de interés nominal
Una tasa de interés nominal es una tasa de interés compuesto que no considera el efecto de la capitalización de los intereses. Suele ser expresada como una razón porcentual en un período de tiempo determinado. También, se suele considerar nominal una tasa expresada como porcentaje con dos bases de tiempo distintas; por ejemplo, una tasa del 10% anual con capitalización mensual. En este caso, la primera de las bases de tiempo, anual, es diferente de la segunda, mensual.
2) Tasa de interés efectiva
Una tasa de interés efectiva es una tasa de interés compuesto que sí considera el efecto de la capitalización de los intereses. Suele ser expresada como una razón porcentual con dos bases de tiempo iguales. Para realizar cálculos, las tasas que se introducen en la ecuación 2.1 deben ser siempre efectivas para que los resultados sean correctos. Si se nos da una nominal, debemos convertirla en una efectiva antes de introducirla en la ecuación 2.1.
Supongamos que se te da una tasa de interés del 12% anual con capitalización anual. Según las definiciones que acabo de presentar, ésta sería una tasa efectiva porque el dato en sí mismo menciona dos bases de tiempo: una anual y la otra también anual. La primera que se indica siempre se conoce como** período de referencia (PR)**; la segunda, como período de capitalización o período de composición (PC).
Supongamos ahora que te topas con una tasa de interés del 27% anual con capitalización cuatrimestral. ¿Qué significa esto?
En este caso, el período de referencia es anual mientras que el de capitalización es cuatrimestral, por lo que, en primera instancia, es una tasa nominal. Pero para entender el significado exacto, debes verificar primero cuántos períodos de capitalización están contenidos en el período de referencia, es decir, cuántos cuatrimestres entran en un año: 12 meses / 4 meses = 3. En consecuencia, quien te ofrezca esa tasa se compromete a agregar el 27% dividido entre 3 ó, equivalentemente, el 9% del capital acumulado hasta ese momento cada cuatro meses, por año. La tasa efectiva correspondiente en este caso es del 9% cuatrimestral con capitalización cuatrimestral. En la práctica, las tasas efectivas tendrán ambas bases de tiempo iguales; las nominales, diferentes.

Ejemplo hipotético 2.3
¿Qué indica un interés del 30% anual con capitalización trimestral? Esboza un diagrama de flujo de efectivo con esta tasa, pero agrega la erogación (desembolso) de dos pagos semestrales iguales.
En este caso, hay cuatro trimestres en un año (12 meses / 3 meses = 4). Como la segunda base de tiempo de la tasa dada es trimestral, cada tres meses se sumará al capital acumulado el 30% / 4 = 7,5% de ese capital.
En la Figura 2.1, se muestra el diagrama de flujo de efectivo. Nota que se indica cada período de pago (PP) o momento en el que ocurre un flujo de efectivo. Como los pagos son desembolsos de dinero, las flechas apuntan hacia abajo, y ocurren cada semestre, o cada dos trimestres. Las líneas verticales punteadas en azul, por su parte, representan los momentos en que se cumple cada período de capitalización (un trimestre).
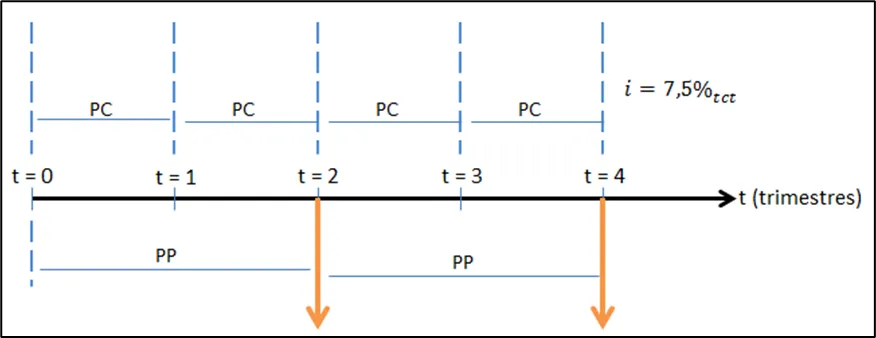
Figura 2.1
La Figura 2.1 permite aclarar que los pagos no necesariamente tienen que ocurrir en el mismo instante en que ocurre la capitalización, es decir, que PP puede ser diferente de PC. De hecho, esta situación es algo bastante común en la práctica.
Algunas convenciones que usaré en lo sucesivo
Los intereses, en la práctica, pueden ser adelantados o vencidos. En esta serie, salvo que explícitamente se indique lo contrario, asumiremos que los intereses son vencidos, es decir, que se devengan o se pagan al final de cada período de capitalización, no al inicio. Además, usaremos una nomenclatura particular para expresar las tasas de interés compuesto.

Tasas de interés equivalentes
Dos tasas de interés son equivalentes si representan la misma velocidad de crecimiento del dinero. En otras palabras, dos capitales iniciales iguales invertidos en el mismo instante a estas dos tasas diferentes generan el mismo valor final, si éstas son equivalentes.
Consideremos dos tasas diferentes, *ixcx * e iycy (para cada una, el período referencial y el de capitalización son iguales), pero con el período de capitalización de la primera mayor que el de la segunda, es decir, tales que x>y. La ecuación (2.3) las relaciona:
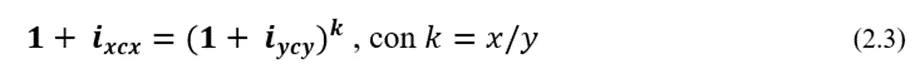
**Ejemplo hipotético 2.4
**
¿Qué tasa efectiva anual es equivalente a un interés del 〖15%〗_acm^ ?
De acuerdo con la nomenclatura y conceptos vistos anteriormente, se pide entonces encontrar la tasa i_aca que equivale a una tasa de interés vencido del 15% anual con capitalización mensual.
Antes de aplicar la ecuación 2.3 para hallar la tasa equivalente, es necesario expresar la tasa dada de manera que su período referencial y su período de capitalización sean iguales. Lo más lógico en este caso es transformarla a una tasa mensual con capitalización mensual.

Tasas de interés continuas
Si el período de capitalización sólo puede tomar valores específicos de tiempo (años, semestres, bimestres, meses, días, etcétera), la tasa es de interés compuesto discreto. Si el período de capitalización es “infinitesimalmente pequeño”, hablamos de una tasa de interés compuesto continuo.
Dicho de otra forma, un período de capitalización que puede tomar cualquier valor dentro de un intervalo y no sólo valores específicos deriva en una tasa de interés compuesto continuo.
Hablar de un período de capitalización infinitesimalmente pequeño es equivalente a decir que el número de períodos de capitalización crece indefinidamente o es “infinitamente grande”. Si aplicamos los razonamientos matemáticos pertinentes, podríamos deducir una ecuación de interés compuesto continuo a partir de la ecuación (2.1):

La tasa de interés compuesto continuo puede calcularse a partir de una de interés compuesto discreto aplicando la ecuación (2.5):

Este tipo de conceptos se aplica para aprovechar las técnicas del cálculo infinitesimal (derivadas, integrales) en el desarrollo de teorías financieras más complejas.
Referencias
Blank, Leland y Tarquin Anthony (2006): Ingeniería Económica. Sexta edición. Editorial Mc. Graw Hill, México.