Nachdem wir mit Fraktale - Dimensionen in der klassichen Geometrie uns der einfacheren Dimensionsbegriffe, die der Algemeinheit wohl bekannter sein dürfen angenommen haben,
wollen wir uns dieses Mal wie schon Angekündigt den fraktalen Dimensionsbegriffen widmen,
damit wir endlich eine Lösung für das Problem der Kochkurve (𝐿(𝐴)= ∞ aber 𝐹(𝐴)= 0) haben
und nebenbei die Dimensionen alle weiteren Fraktale aussagekräftiger angeben können.

Ähnlichkeitsdimension
Am einfachsten lässt sich aus den klassischen Dimensionsbegriffen die Ähnlichkeitsdimension ableiten.
Dafür wollen wir uns zunächst anschauen,
was mit Objekten der klassischen Geometrie bei Skalierung passiert.

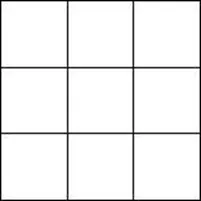

Wer selbst kurz tüfteln möchte, auf welche Weise Dimension, Anzahl und Skalierungsfaktor
sich in eine Formel verpacken lassen ist natürlich herzlich aufgefordert dies zu tun.
Es sollte auch nicht allzu schwer sein.
Spoiler
Die Formel:
𝑎= 𝑠^𝐷
nach der Anwendung diverser Logarithmen Gesetzen erhalt man:
𝐷= log(𝑎)/log(𝑠)
Vorraussetzung, dass man die Ähnlichkeitsdimension eines Objekts bestimmen kann ist,
dass dieses eine exakte Selbstähnlichkeit aufweist
d.h. als Zusammensetzung aus mehreren Kopien des Objekts selbst interpretiert werden kann.
Anders ausgedrückt: Das Objekt lässt sich si ein Teilen, das jeder der Teile dem ganzen Objekt entspricht.
Die Formel die man im Allgemeinen findet ist folgende:
𝐷= log(𝑁)/log(1/𝜀) bzw.
𝐷= −log(𝑁)/log(𝜀)
Sie besteht aus der Anzahl verkleinerter Versionen N und dem Skalierungsfaktor 𝜀<1,
weshalb das Vorzeichen hier auch negativ ist im Gegensatz zu der oben erarbeiteten Formel.
Am 1915 von Wacław Franciszek Sirpiński (poln. Mathematiker 1882-1969) erfundenen
Sierpińksi Dreieck lässt sich besonders schön zeigen,
wie sich die Ähnlichkeitsdimension berechnen lässt.

Wie man erkennt besteht es aus 3 kleineren Kopien des Ganzen die jeweils um 0.5 verkleinert wurden.
Also N= 3; 𝜀= 0,5
Somit ergibt sich für das Sierpińksi Dreieck die Ähnlichkeitsdimension
𝐷= −log(3)/log(0,5)= 1,5849625...
Somit haben wir eine erste Methode erarbeitet, mit denen man, zumindest bei exakt Selbstähnlichen Objekten (übrigens nicht nur der fraktalen sondern auch der klassischen Geometrie),
einen aussagekräftigen Dimensionswert zuordnen kann.
Jedoch gibt es immernoch Objekte, für die man mit dieser Methode
keine aussagekräftige fraktale Dimension angeben kann.
Für das in Fraktale III - Großbritanniens Küstenlinie beschriebene Problem mit der Maßfindung
für die Küste Großbritanniens ist hiermit jedoch noch keine Lösung gefunden.
Somit müssen noch andere Definitionen her, denen wir uns aber das nächste Mal widmen wollen.
Zum Abschluss noch eine kleine Aufgabe für euch:
Auch für die, von mir oft als Besipiel herangezogene, Koch-Kurve lässt sich ein Dimensionswert mit Hilfe der Ähnlichkeitsdimension festlegen. Viel Spaß bei der Ausarbeitung, Lösungen gerne in die Kommentare.
Kleiner Tipp: Lösungen googlen und in die Kommentare packen, statt es selber auszuarbeiten,
macht nur halb so viel Spaß, zumal es nicht allzu schwer ist.
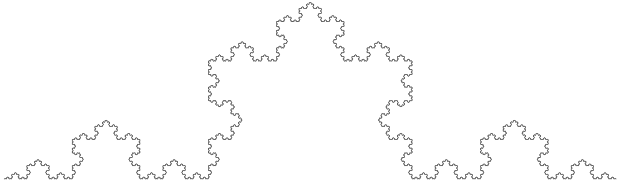
Koch-Kurve