
Hello everyone. I would like to start a math topic series here with the hope of helping who needs.
I will start with constructing real numbers. Many prefer starting with natural numbers but since i am not an expert of set theory i will construct the rest number sets with the help of real number.
Real numbers is not just a set. It is a structure that includes addition, multiplication and inequality. Not to dive into much complexity and confuse readers i also prefer adding zero and one in this structure. We will discuss zero and one much more detailed when we start doing some group theory.
Real numbers is a structure, 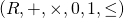 , that satisfies the following axioms. (Note that, if not mentioned spesifically, every element in the structure satisfies these axioms)
, that satisfies the following axioms. (Note that, if not mentioned spesifically, every element in the structure satisfies these axioms)
A1: 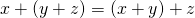
A2: 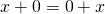
A3: For every 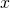 there exists
there exists 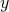 such that
such that 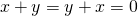
(A3) Observe that by using A1 and A2 for a given 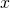 ,
, 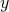 is unique. And we will denote that
is unique. And we will denote that 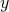 as
as 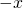 .
.
A4: 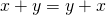
Now axioms for multiplication. We will denote 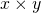 as
as 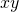
M1: 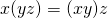
M2: 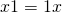
M3: For a given 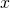 different than zero, there exist
different than zero, there exist 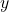 such that
such that 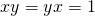 (Also is unique and we will denote
(Also is unique and we will denote 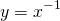 )
)
M4: 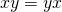
AM: 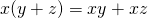 and
and 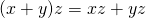
Observe followings;
i) 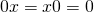
ii) 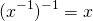 , where
, where 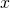 is not equal to zero.
is not equal to zero.
iii) 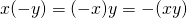
iv)If 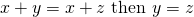
v) 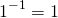
vi) 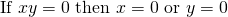
And last part of axioms.
O1: 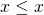
O2: 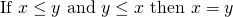
O3: 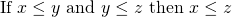
O4: 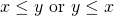
AO: 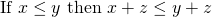
MO: 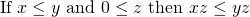
Note that rational number structer also satisfies these axioms. So we need a specific axiom that characterize real numbers.
Definition: Let  be a subset of Real numbers. If, for every element
be a subset of Real numbers. If, for every element  in
in  , there exists a real number, say
, there exists a real number, say  , such that
, such that 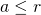 then we say
then we say  is upper bound of A
is upper bound of A
Sup axiom : Any proper(not empty) subset of real numbers, that has upper bound, has a least upper bound.
We call that least upper bound a supremum or sup. So;
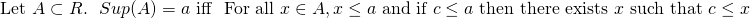 . Please generate some examples. Note that, supremum of a set should not necessarily be in that set.
. Please generate some examples. Note that, supremum of a set should not necessarily be in that set.
So we say, a sturcture is a Real Number structure if it satisfies these axioms.
Next time i am planning to show an example of an arbitrary irrational number is belonging to this system by using these axioms.
Thats all for now. Thanks for reading :)