
Hello its a me again Drifter Programming! Today we will get into Java again talking about the already mentioned Bellman-Ford algorithm that is used for finding Single-Source Shortest Paths in Graphs. You can check out the Dijkstra algorithm for the same problem here! So, let's get started!
Bellman-Ford Algorithm:
The Bellman-Ford algorithm as I already mentioned in the post about Dijkstra and also the quick introduction in the start of this post is used for finding shortest paths when starting from a specific source vertex. The difference between those 2 algortihms is that Dijkstra doesn't work with negative weights and Bellman-Ford works and also detects negative-weight circles that make the algorithm iterate for ever and never find the best path, cause there will always be a better one.
Because, of this extra checking for negative-weight circles the algorithm has a slight decrease in performance when comparing it to the Dijkstra algorithm.
So, how does the algorithm work?
Well, it's pretty similar to the Dijkstra algorithm, but iterates through all edges repeatedly. We will again store the distances and parents (or predecessors) in an array inside of the algorithm/function. We then initialize those two arrays having a value of infinity (maximum float value for us) and predecessors equal to -1 for all vertices, except the source vertex that will have a distance of 0 to itself. We then iterate through all the edges repeatedly for vertexCount - 1 times and check (as in Dijkstra) if the distance of the startingPoint u + the weight of the edge (u, v) is less than the already been set distance of the endingPoint v. If that is true then we set the new distance of v to distance of u + weight of edge (u, v) and also set u as the predecessor of v. This is the part where we might have a negative-weight circle. To check for negative-weight circle we use the same equation dist(u) + w < dist(v) and if it's true again then the graph contains a negative-weight circle, cause vertexCount - 1 iterations already gave us the shortest paths!
Pseudocode from wikipedia:

We will implement the same pseudocode, but in Java there will be some changes that we already know how to do from previous Graph Algorithms and also mentioned earlier.
Bellman-Ford Java implementation:
To implement this algorithm we will use the Graph implemenation that uses Adjacency Lists (or Priority Queues) and also the Edge class/object that we used in Dijkstra. We don't need a separate Vertex class/object something that was actually not needed in Dijkstra as well, cause we can also just use the arrays with the distances and predecessors.
So, our classes/objects look like this:
Edge class:

Graph class:

The algorithm for Bellman-Ford looks like this:

And is inside of the TestGraphs class:
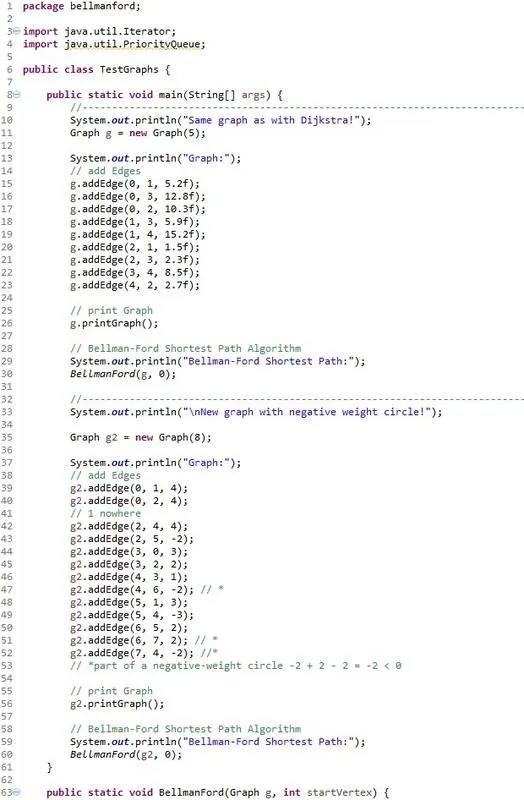
We ran the same graph example as with Dijkstra and got the same result and I also added a second Graph that contains a negative-weight circle and saw that the algorithm detected it.
The console printed out:

Here the Java Codes in pastebin:
TestGraphs/BellmanFord Algorithm class
Don't forget to remove the package declaration or you can also create and put the classes inside of a package with the name "bellmanford"!
And this is actually it!
Next time in Java Graphs we will get into 2 algorthims (Floyd-Warshall and Johnson) that are used for finding all-pair shortest paths!
Bye!
