
확률계산에서 Random 변수가 어떤 중요한 역할을 하는지 주사위 게임을 통해 알아보자.
주사위 굴리기 게임에서 나올 수 있는 결과(outcome)에 따른 Random한 변수를 대문자 X로 표기한다. 주사위 굴리기에서 나온 주사위 면의 점의 수가 i 일 때에 실제 숫자 값 i로 처리해 두면 자연스럽게 Random 변수 X가 될 수도 있다. 하지만 반드시 그런 것만은 아니다. 예를 들어 주사위 면에서 점의 수가 몇 개이든 모조리 0으로 두어 처리할 수도 있으며 이 또한 Random 변수 Y 로 둘 수 있는 것이다. 또는 좀 이상스런 경우이지만 주사위 면의 점의 수 i가 짝이면 2i 홀이면 –i 인 Random 변수 Z로 둘 수도 있는 문제이다.
즉 이벤트 공간 F에서 발생하는 특정 이벤트에 대해 숫자를 부여하여 처리할 수 있다는 점이다. 어떤 전문가는 이런 과정을 이벤트 공간으로부터 숫자적으로 추상화 시키는 과정이라고도 어렵게 말하는데 그냥 일어난 이벤트 상태에 대해 숫자로 처리해버린다 또는 숫자 개념의 상금이 얼마라는 개념으로 정리해버리면 될 듯하다.
한편 주사위 굴리기 게임에서 주사위 면의 점의 수가 홀이면 “1” 아니면 “0”이 되도록 Random 변수를 잡을 수 도 있다. 이런 양면적 Random 변수를 전문 용어로 “indicator” 변수라고도 하는데 어떤 특정한 이벤트가 발생했는지 여부를 체크하는데 실제로 많이 이용된다.
따라서 Random 변수 X가 값 a를 가지게 되는 확률을 P(X=a) 또는 Px(a)로 표기하도록 하자. 아울러 Random 변수 X 의 범위는 Val(X) 로 나타내자.
Dice(주사위) Example: 그렇다면 주사기 굴리기 게임에서 던진 후 나올 수 있는 결과(outcome) 에 대해 Random 변수 X를 설정하면 즉 Random 변수 X에 대한 확률 분포는 다음과 같이 표현이 가능하다. Px({1}) = Px({2}) = Px({3}) ⚫⚫⚫ = 1/6
쉽게 알 수 있는 내용을 일부러 어렵게 표현하는게 수학이라고 심한 불평을 했다는 사람이 그 유명한 아인슈타인이라는 얘기를 들은 적이 있는데 사실인 듯 하다. 아인슈타인하면 상대성이론과 양자역학 양 분야에서 전대 미문의 업적을 성취했으나 정작 본인 자신은 확률분포만 집중적으로 캐는 양자역학 분야를 꺼려했는데 그 이유는 바로 이 통계확률의 특성 때문 아닐까요? 머신 러닝에서도 그런 냄새가 많이 나는 편인데 가능하면 모두 아인슈타인 편에 서도록 해야 할 것 같다. 알기 쉬운 기본 정도만 공부하고 골치 아픈 분야는 아예 피하는게 상책인 듯하다.
앞서 이벤트 공간에서 설정했던 확률 분포 P({1}) = P({2}) = P({3}) ⚫⚫⚫ = 1/6 과는 어떤 차이점이 있는 것일까? 이 여섯 개의 항을 서로 비교하면 값은 같지만 이벤트 공간과 결과물(outcome) 공간이 같지는 않으므로 뭔가 다르다는 뉴앙스가 있는듯하다. 그러므로 확률분포는 처음에 어떻게 정의하여 사용할 것인지 주의해야 한다.
Dice and Coin Example: 주사위 outcome space에서의 Random 변수 X, 아울러 동전 던지기에서 앞면이 나오면 +1 뒷면이 나오면 0 의 값을 가지는 indicator 변수 Y(이것도 Random 변수임)로 두고 합성확률 (Joint Distribution of X and Y) P(X, Y)를 계산해 보자. 주사위 굴리기 와 동전 던지기는 별도의 독립적인 확률 게임이 될 수 있으며 아래와 같이 2차원 형태의 확률 계산이 가능해 진다.

합성 확률 P(X,Y)는 구체적으로 P(X=a, Y=b) 또는 Pxy(a, b)로도 표기할 수 있다.
이와 같은 합성확률의 구체적인 사례는 6개의 입자에 대한 볼츠만 분포 확률계산에서 9단계 에너지레벨 모델을 사용하여 아래와 같이 macrostate 별로 microstate 수를 카운팅한 표에서 작성이 가능하다. 이 표에서 microstate 수는 각 입자들이 서로 구별 가능하다는 조건하에서 얻어지는 Random 변수로 볼 수 있으며 나올 수 있는 전체 결과물(outcome) 범위도 명확하다. 반면에 macrostate 수도 단지 전체 에너지 값을 일정하게 지키는 범위 내에서 에너지 레벨별로 입자가 분포하게 되는 경우의 수로서 나올 수 있는 전체 결과물(outcome) 범위도 명확한 Random 변수로 볼 수 있다.
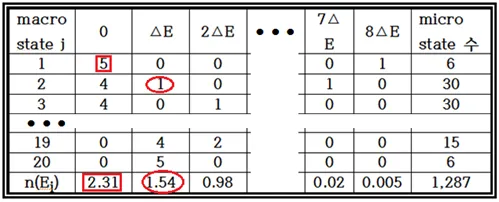
이 표에서 숫자 0, 1, 2, 3, 4, 5 는 에너지 레벨에 분포하는 입자 수를 의미하므로 총 입자수 6으로 나누어 주면 쉽게 확률분포로 바꿀 수 있다.
아울러 전체 에너지가 8⧍E 로 일정하다는 조건하에서 얼마나 많은 입자들이 특정 에너지 레벨에 있을지는 macrostate 별 각 에너지 레벨마다 계산이 가능하다. 즉 macrostate 1 에서 E0 = 0 레벨에 가장 있을 듯한(probable) 입자의 수는 5X(6/1237)=0.023 개로 계산된다. E0 = 0 레벨에 대해서 20개의 macrostate 별로 계산하여 합하면 n(E0)=2.31을 얻을 수 있다. 동일한 방법으로 0, ⧍E, 2⧍E, ⦁⦁⦁,8⧍E 에너지 레벨까지 계산이 가능하며 표의 마지막 줄에 결과가 출력되어 있다. 결국 입자들이 가장 있을 법한 에너지 레벨 별 입자 수를 다 더한 마지막 줄의 결과들 즉 2.31, 1.54, 0.98, ⦁⦁⦁을 총 입자수 6으로 나누면 아래와 같이 에너지 레벨별 전체 확률분포 값이 표로 계산된다.
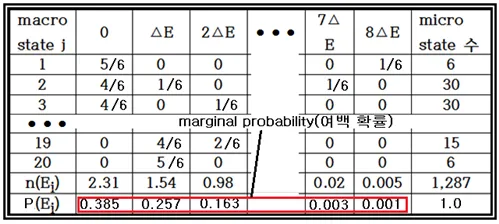
이 확률 표에서 에너지 레벨 별로 합산한 확률 즉 0.385, 0.257, 0.163, ⦁⦁⦁들을 여백 확률(marginal probability) 이라 한다.
Conditional Probability Distributions(조건부 확률분포)을 정리해 보기로 하자. 다른 Random 변수의 값이 알려진 상황 또는 이벤트가 알려진 상황 하에서 우리가 고려하는 Random 변수의 확률분포를 나타낸다. 예를 들면 Random 변수 Y =b 가 이미 정해졌을 때 Random 변수 X= a 가 일어날 확률을 다음과 같이 표현한다. 특히 뒷부분의 표현이 나누기이므로 Y=b 가 일어날 확률이 0일 때는 제외한다.
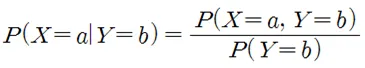
이러한 조건부 확률 개념은 위에 제시한 6개 입자의 볼츠만 확률 표에서 쉽게 예를 찾아 볼 수 있다. 즉 “macrostate 2인 경우에 적어도 에너지 레벨 ⧍E에 입자가 1개가 있는 microstate 의 경우의 수” 와 같은 예를 들 수 있을 것이다.
예제: 주사위를 굴려서 홀(odd)이 나올 이벤트 즉 {1,3,5}인 경우에 한해서 다시 주사위를 굴려 “1”이 나오게 될 확률을 계산해 보자. 웬지 쉬운 문제를 가능하면 까다롭게 만드는 듯한 느낌이 든다.
Random 변수 Y 가 홀 즉 {1,3,5}중에서 하나의 수가 나올 확률은 즉 P(Y=odd)=(1/2)이다. Y 가 일어난 이후에 다시 주사위를 굴려 다시 Random 변수 X가 “1” 이 나오게 될 확률은 여전히 (1/6)이다.
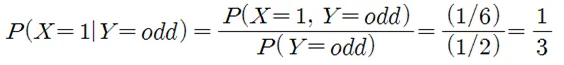
볼츠만 확률분포 아이디어를 차용한 머신 러닝 softmax 명령에서 조건부 확률분포 얘기가 흔하게 나오므로 그때 다시 체크해 보기로 한다.