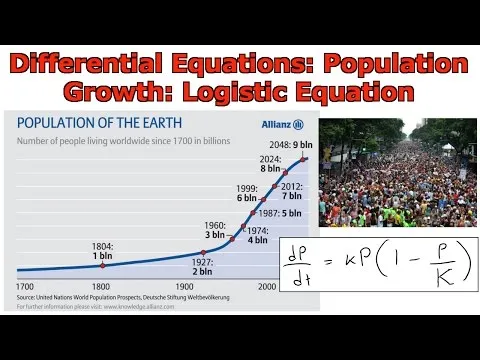
In this video I go over the logistic differential equation, which is a more advanced version of the simple population growth exponential model that I went over in my earlier videos. The basic model involved the assumption that the growth rate is proportional to the population size but this is only true if the population size is small. As the population size gets larger, a relative growth rate decreases as it approaches the carrying capacity, which is the largest population size that can be maintained in the long run. If the population size ever gets larger than the carrying capacity, then the growth rate becomes negative since the environment won't have enough resources to maintain too large a population. The logistic equation takes all of these factors into consideration and it is written in terms of the differential equation:
dP/dt = kP(1 - P/K)
Where P is the population size, k is the proportionality constant, and K is the carrying capacity.
In my later videos I will build upon this logistic equation as well find solutions for such equations, so stay tuned for those!
Watch on DTube:
Watch on BitChute:
Download PDF Notes: https://1drv.ms/b/s!As32ynv0LoaIhtQWBtWhfGWVHv4AWg
View Video Notes Below!
Download These Notes: Link is in Video Description.
View These Notes as an Article: https://steemit.com/@mes
Subscribe via Email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donateReuse of My Videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight Back Against Censorship:
- Bookmark sites/channels/accounts and check periodically
- Remember to always archive website pages in case they get deleted/changed.
Join my private Discord Chat Room: https://mes.fm/chatroom
Check out my Reddit and Voat Math Forums:
Buy "Where Did The Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
Follow My #FreeEnergy Video Series: https://mes.fm/freeenergy-playlist
Watch my #AntiGravity Video Series: https://mes.fm/antigravity-playlist
Follow My #MESExperiments Video Series: https://mes.fm/experiments-playlist>
NOTE: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (If Available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed. (#Try2xSpeed)
-- Try 4X+ Speed by Browser Extensions, HookTube.com, Modifying Source Code.
-- Browser Extension Recommendation: https://mes.fm/videospeed-extension- Download and Read Notes.
- Read notes on Steemit #GetOnSteem
- Watch the video in parts.
Differential Equations: Population Growth: The Logistic Equation
The logistic model is a more sophisticated model for population growth than the basic exponential growth model that I covered in my earlier videos.
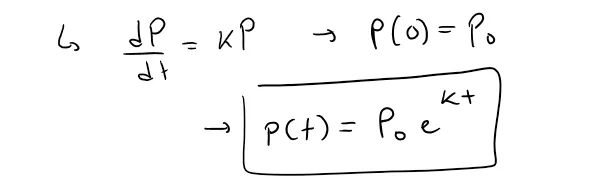
In developing this more advanced logistic model, I will use the concepts I covered in my earlier videos, namely:
- Direction Fields
- Euler's Method
- Explicit solution of separable equations
The Logistic Model
As explained in my earlier videos, a population often increases exponentially in its early stages but levels off eventually and approaches its carrying capacity because of limited resources.
If P(t) is the size of the population at time t, we assume that:
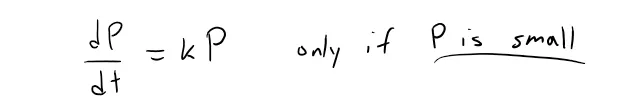
This says that the growth rate is initially close to being proportional to size.
In other words, the relative growth rate is almost constant when the population is small.

But we also want to reflect the fact that:
- The relative growth rate decreases as the population P increases
- The relative growth rate becomes negative if P ever exceeds its carrying capacity K
-- K is the maximum population that the environment is capable of sustaining in the long run.
The simplest expression for the relative growth rate that incorporates these assumptions is:
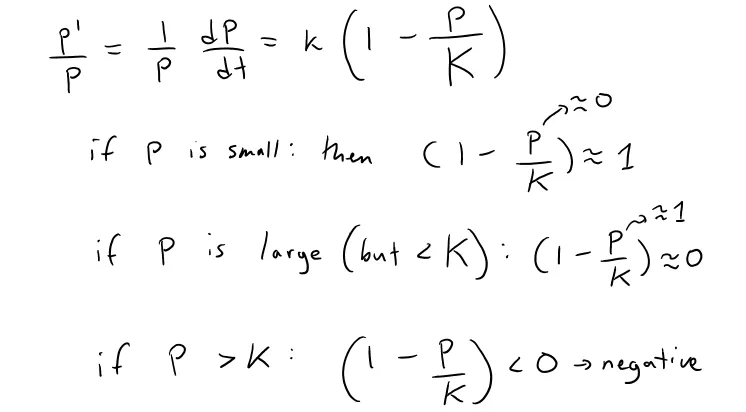
Multiplying by P, we obtain the model for population growth known as the logistic differential equation:
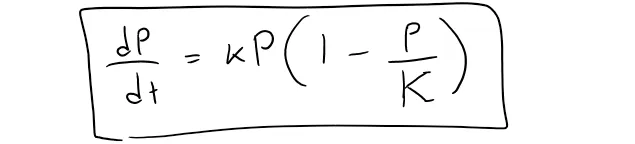
Notice from this equation, that if P is small compared with K, then P/K is close to 0 and so:
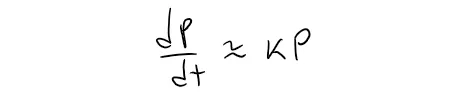
However, if the population approaches its carrying capacity, then:

We can deduce information about whether solutions increase or decrease directly from the logistic equation:
- If population P lies between 0 and K, then the right side of the equation is positive, thus dP/dt > 0 and the population increases.
- If the population exceeds the carrying capacity (P > K), then 1 - P/K is negative, and so dP/dt < 0 and the population decreases.