It was a good long break we had for this collaborative project on Hive, but we're back on track. It was great to know that I am still familiar with what we did from the previous episode of this project since this week's tasks are an extension to the simulation we've done a month ago.
This project is headed by @lemouth, our professor 🧑🏻💻 and resident particle physicist in the StemSocial community. The focus of this work is the simulation of a signal typical of neutrino mass models at CERN's Large Hadron Collider (LHC). In the Standard Model of elementary particles, neutrinos are considered massless; however, as observed in experiments, these particles are massive. And that is what we're trying to address in this project, there must be new particles responsible for the origin of the neutrinos' masses. We look into these new particles as they yield specific signals at particle colliders. Our reference article that is also authored by @lemouth has considered such signal for collisions producing a pair of particles called (anti)muons. We extend this by considering other pair of particles such as electrons, positrons or even by a mixed pair including one muon and one electron or one antimuon and one positron. There's a lot of exciting work to do! And if by any chance, this has caught your interest, it would be great to have you onboard. :)
Just a recap on what we have done so far:
- Installation of the tools [MG5aMC] necessary for particle physics simulation
- Using the MG5aMC to simulate top quark production at CERN's LHC
- Installation and use of MadAnalysis 5 for detector simulation and event reconstruction
- Investigating top quark production at CERN's LHC using MadAnalysis 5
- Exploring a neutrino mass signal at CERN's LHC using MG5aMC.
And for this week's tasks, we go back to the process we have considered, whereas protons are collided inside the LHC. At high energies, the constituents of protons or the quarks scatter during collision. These initial quarks emit a very energetic W boson by virtue of the weak force. The two W bosons interact with each other by an exchange of a heavy neutrino N, which is responsible for generating the masses of the neutrinos of the Standard Model as proposed in our model. This exchange produces a pair of leptons of the same electric charge, as mentioned, the reference article considered the case where these two leptons are either two muons or two antimuons.
The calculation of the production rate associated with the above signal is a perturbative calculation. From the earlier episodes of the project, it was mentioned that our calculations will concern infinite series. Calculation of an infinite series is impossible to do, at some point, we only need to consider some terms. The first term is the dominant one, which was what we have calculated from the previous episode. We call this leading-order calculation as we have ignored all the terms except the leading one. Our work for this week is to determine the uncertainties due to missing higher-order terms.
The next installation of citizen science will be the performing the laborious next-to-leading-order calculation, which is not easy to handle numerically, as it deals with infinities that cancel each other. In doing this, we include more terms and in return, we expect that this will reduce the uncertainties we have calculated this week.
Let's get started!
We start by running MG5aMC in the terminal with
./bin/mg5_aMC assuming that you're already on your working directory. The commands below were the similar ones we use from the fifth episode.MG5_aMC>import model SM_HeavyN_NLO
MG5_aMC>define p = g u c d s u~ c~ d~ s~
MG5_aMC>define j = p
MG5_aMC>generate p p > mu+ mu+ j j QED=4 QCD=0 $$ w+ w- / n2 n3
MG5_aMC>add process p p > mu- mu- j j QED=4 QCD=0 $$ w+ w- / n2 n3
MG5_aMC>output espresso_lo
The next step is to recalculate the leading-order production rate associated with our signal and this time, we include the estimated uncertainties inherent to the calculation. Similar with how we used MG5aMC previously, we will configure the neutrino model we considered by tuning the parameters necessary. By launching the model, we modify the param_card.dat and run_card.dat as specified in this week's tutorial blog
Here are results I've got for the first run, where the mass considered for the heavy neutrino is 1000 GeV. The additional information we got here are the two uncertainties, scale variations and PDF variations. Calculating for the total uncertainties, we add these number in quadrature, thus getting the results of 0.01393 pb with an upper uncertainty of 12.32% and a lower one of 10.76%.
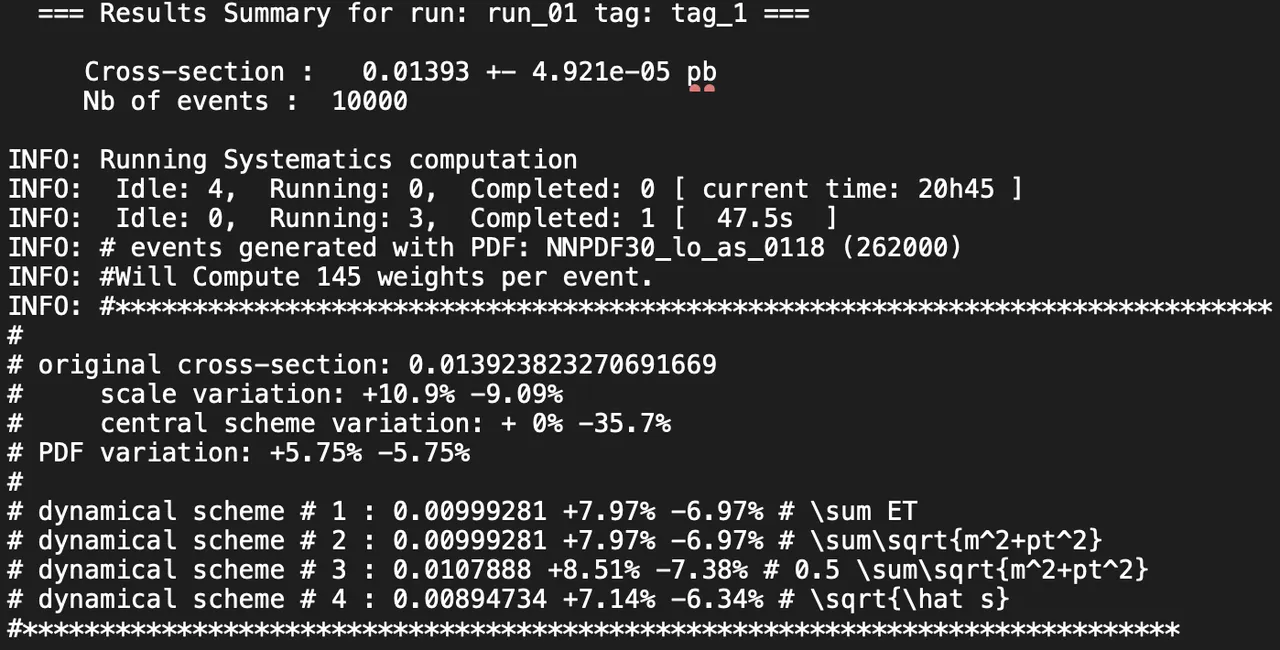
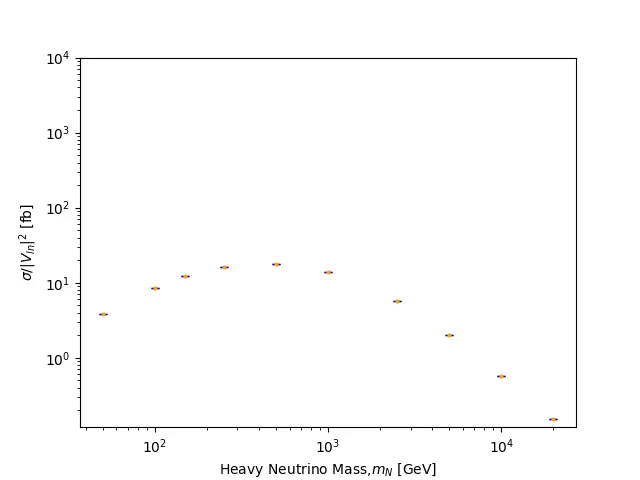
The remaining part of this week's tasks is to consider different masses of the heavy neutrino. Again, I have used the same mass values and let my computer do all the hard work of calculating the cross sections rates and uncertainties.
Signal rate dependence on the neutrino mass at 13.6 TeV
| Neutrino mass (GeV) | Cross section (fb) | Error |
|---|---|---|
| 50 | 3.843 | ±0.00892 |
| 100 | 8.576 | ±0.0237 |
| 150 | 12.23 | ±0.0405 |
| 250 | 16.14 | ±0.0560 |
| 500 | 17.80 | ±0.0578 |
| 1,000 | 13.91 | ±0.0455 |
| 2,500 | 5.69 | ±0.0167 |
| 5,000 | 2.02 | ±0.0038 |
| 10,000 | 0.57 | ±0.0014 |
| 20,000 | 0.15 | ±0.00019 |
The plot below shows the signal rate dependence on the neutrino mass. I have included error bars, it looks like the error bars in the x-axis, but it's actually the caps of the error bars in the y-axis.
Estimated uncertainties of the production rate for neutrino masses at 13.6 TeV
| Neutrino mass (GeV) | Scale variation | PDF variation | Total uncertainty |
|---|---|---|---|
| 50 | 2.56% -2.67% | 5.87% -5.87% | 6.40% -6.45% |
| 100 | 3.87% -3.73% | 5.78% -5.78% | 6.96% -6.88% |
| 150 | 4.89% -4.56% | 5.82% -5.82% | 7.60% -7.39% |
| 250 | 6.34% -5.69% | 5.72% -5.72% | 8.54% -8.07% |
| 500 | 8.57% -7.40% | 5.71% -5.71% | 10.30% -9.35% |
| 1,000 | 10.80% -8.99% | 5.72% -5.72% | 12.22% -10.66% |
| 2,500 | 13.50% -10.90% | 5.90% -5.90% | 14.73% -12.39% |
| 5,000 | 15.00% -11.90% | 6.02% -6.02% | 16.16% -13.34% |
| 10,000 | 15.60% -12.30% | 6.16% -6.16% | 16.77% -13.76% |
| 20,000 | 15.90% -12.50% | 6.15% -6.15% | 17.05% -13.93% |
As I end this report, with the estimated uncertainties we got and calculation of the total uncertainty, I remember this thought from a journal I read a long time ago. My memory is failing me a little and I can't seem to find the paper from the keywords I vaguely remember, but here's the thought: It's not that physicists don't want uncertainties, what they aim is to quantify those uncertainties and reduce it further.