“触发器”是数字电路中非常重要的基础元素,可以说凡是涉及到时钟与寄存器的,都会涉及到“触发器”。触发器比基本逻辑电路要复杂一些,尤其涉及时序的时候,有时真的让人头大。
而探究触发器归根结底应该从最基本的RS触发器说起,所有的触发器基本上都是基于它而设计出来的。
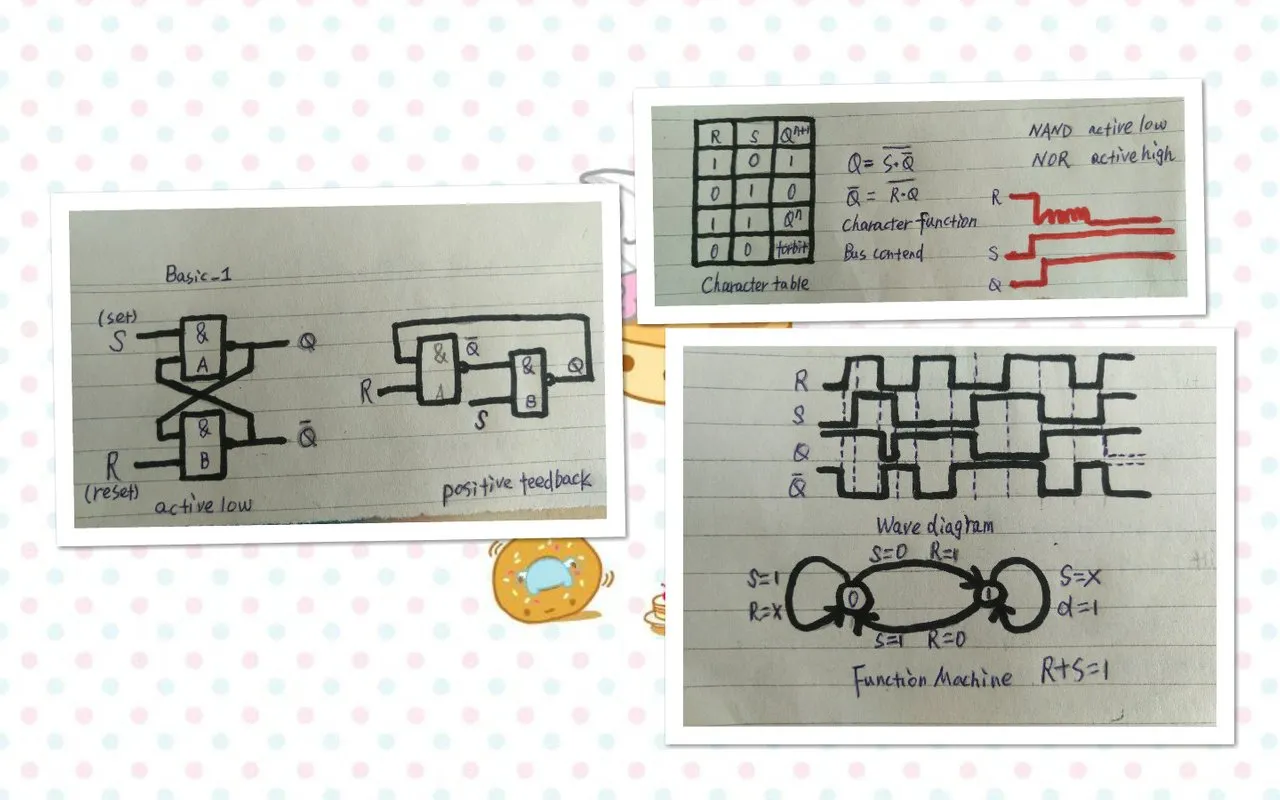
如上图所示,左边一幅图为RS触发器的原理图(素材参考了触发器基本原理一文)。左边为常规画法,右边的画法则比较容易的看出输出到输入的反馈。图中的RS触发器由两个与非门构成,根据它的构成逻辑,我们可以写出它的特性方程(CharacterFunction)(图中右上的图)。可见触发器当前的输出不仅与输入有关,还与输出有关,这个输出,是刚才的输出,我们称它为次态,而我们现在的输出称为现态。
假设这个器件,我们一开始不给它任何操作,一上电,S和R就会为0,S为0会导致Q为1,R为0会导致~Q为1。但是我们设计的初衷是想让这二者为互补的输出,即只要一者为0或1,另一者就为1或0,那该怎么办呢?所以R和S不能为同时为0。这是这个电路的约束条件,即S+R=1。
那么其他情况下呢?比如S=0,R=1,S=0使Q=1,Q反馈回来跟R相与使Q为0,这说明S=0,R=1使Q发生了置1,Q=1是由S=0直接导致的,所以称S=0为置1端。如果S=1,R=0,那么R=0会使Q直接置1,Q反馈回来与S相与使Q为0,所以称R=0为置0端。如果S=1,R=1,我们会发现如果原先Q为1,Q为0,那么Q反馈回来与R相与就会使Q为0,而Q为0反馈回来与S相与仍会使Q为1,也就是说原先Q为1,Q为0,现在仍然如此,结果未变。同理如果原先Q=0,Q为1,那么现在仍然是Q=0,~Q为1,结果不变,说明S=1,R=1会使触发器保持原来的结果不发生改变(retain)。这点也可以根据图中的特性方程得出,并总结为特性表(CharacterTable)所示的结果。且因为我们是S=0使Q=1,R=0使Q=0,所以我们称R、S为低电平有效(Active Low)。
但我们反过来看,如果R、S同时为1,我们并不能知道我们保存的Q值是0还是1,我们需要知道我们原先向里面储存了什么数。有一个根本的问题就是R+S的输入有限制,不能同时为0,万一我的S和R在传输过程中不小心同时为0了会发生什么呢?如上图中右下角的图所示,我们观察它的波形图(WaveTable),如果S和R同时为0,那么Q和Q会同时为1,但如果此时R和S同时变为1,那么理论上Q和Q分别反馈回来与S和R相与就会使Q和Q同时变为0,然后再同时变为1,OMG,这不就是振荡了吗?但实际上由于上下两个门的参数不总是那么一致,所以实际上S和R变为1,总会有先后,并且有可能S在先,也有可能R在先,如果S在先,那么Q会先变为0,致使Q变为1,如果R在先,会使~Q先变为0,致使Q变为1,由于谁在先,谁在后无法人为控制,所以会使S=0和R=0转换到S=1,R=1时由于输入端的“总线竞争”现象而无法预料到输出结果(如图中时序图WaveDiagram的末尾部分)。
同时根据触发器的输出结果以及不同结果间的互化,我们可以得出一种状态之间互相转换的图,我们一般称其为状态机(Function Machine State)。如图中右下角所示,如果触发器当前输出为0,如果要求触发器输出仍为0,只需要S=1,R等于任意值即可,如果需要触发器输出值变为1,则只需要S=0,R=1即可,同理,如果触发器当前状态是1,如果仍需保持1,则只需要R=1,S取任意值即可,如果输出需要变为0,则需要R=0且S=1。
我们这里是以与非门为例进行分析说明的。如果利用或非门也可以构成RS触发器,不过或非门构成的RS触发器,置位或复位都是高电平有效(ActiveHigh),R=0,S=0时是保持,R和S不能同时为1,即约束条件为RS=0。无论是与非门还是或非门构成的触发器,它们都遵守RS触发器的基本规律。
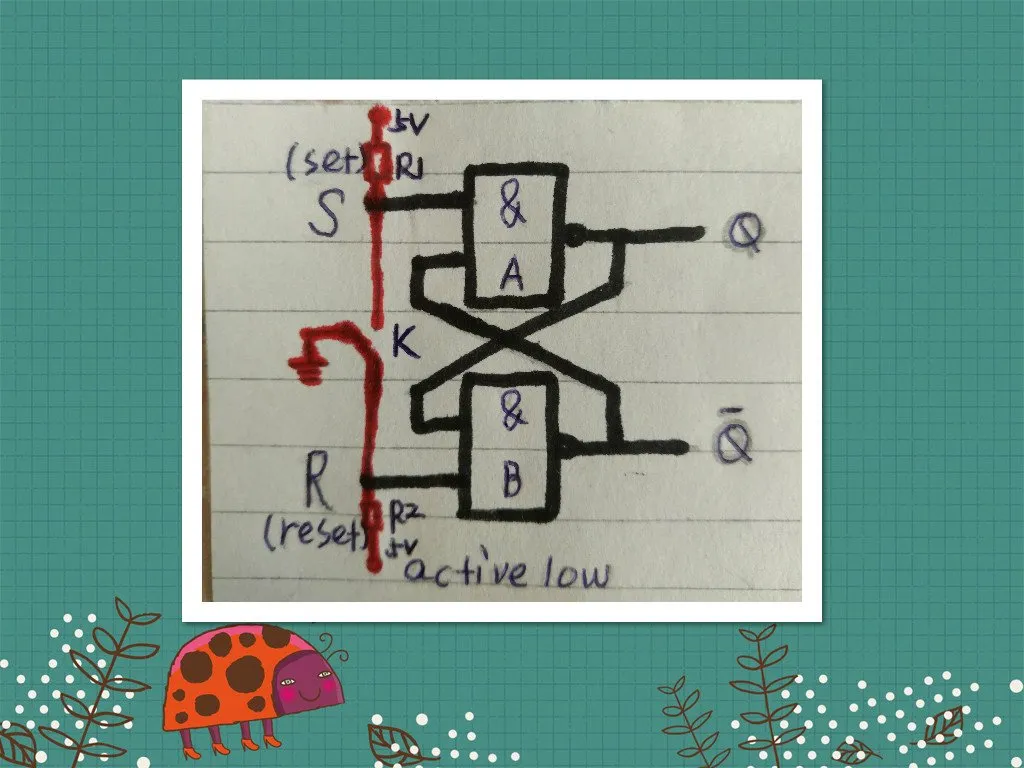
另外,RS触发器有一个妙用就是按键消抖(消除机械开关引起的抖动)。如图中右上部分红色波形曲线(图中的R应为S,S应为R),当开关K使S接高电平,R接地时,输出信号Q为低电平,当开关K使S接地时,R接高电平,K切换到S时会有抖动,但S变为低电平的一瞬间,由于触发器的保持功能,即使S上的电平由于抖动变到1也不会影响触发器的输出结果,当然,重新由S端切换到R端也不会由于抖动而影响输出结果。(如下图所示,图片素材来源于RS触发器是如何实现按键消抖的?)。
但有时我们想有一个信号来控制输入信号,从而希望输入信号能以我们希望的节奏进行输入。基于这种想法,我们在基本RS触发器的基础上加入了控制端,由CP这一信号控制S和R的输入,通常我们把CP称为同步脉冲,因而这种触发器又称为同步RS触发器,如下图所示。
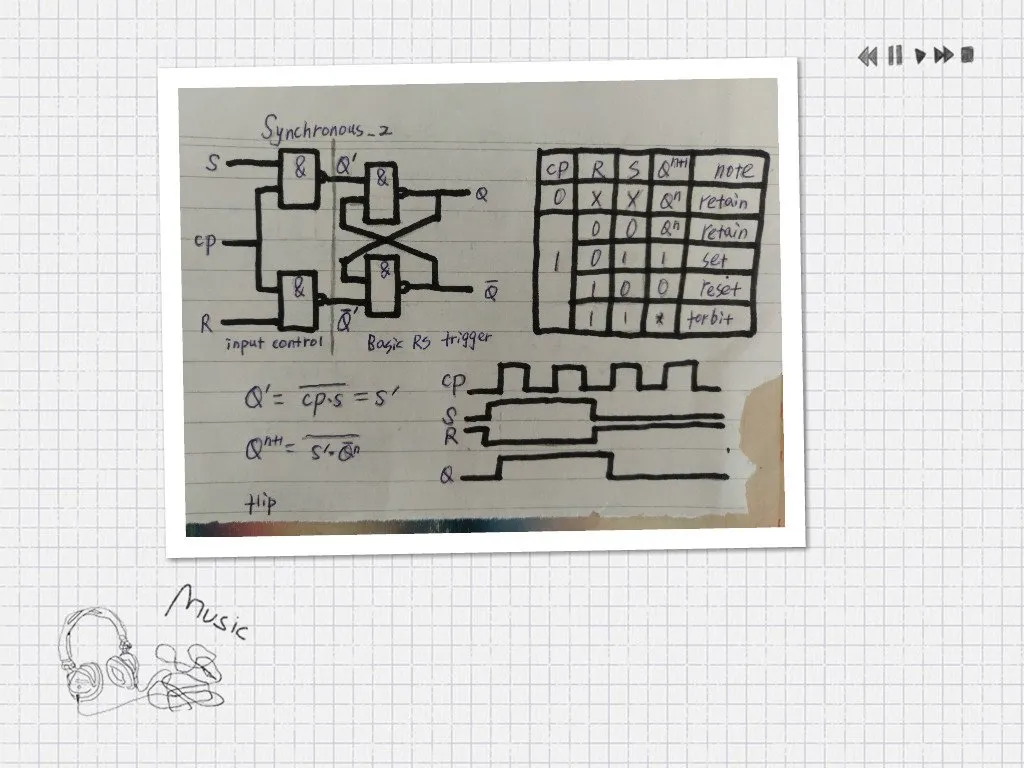
由上图所示,当CP=0时,相当于基本RS触发器的输入恒为R=1和S=1(原来的R和S),所以触发器的输出保持原来的值不变。当CP=1时,则此时CP不会对输入信号产生任何影响,但原来的S等于现在得S了,原来的R等于现在的R,所以原先的S=1,R=1触发器保持不变变成了现在的S=0,R=0触发器保持不变;原先的低电平有效变成了现在的高电平有效;原先不能同时为0变成了现在不能同时为1(如图中的特性表所示)。除此之外与基本RS触发器并没有其它的区别了。
但我们会发现在CP=1时,S和R的变化会直接反映到输出上。如果CP=1的时间过长,那么就失去了对S和R的控制作用,这种现象叫做“空翻”,这不是我们想要的。我们想要的是在一个时钟周期内,输出信号只根据S和R变化一次。因而我们需要对它再进行改进,如下图所示。
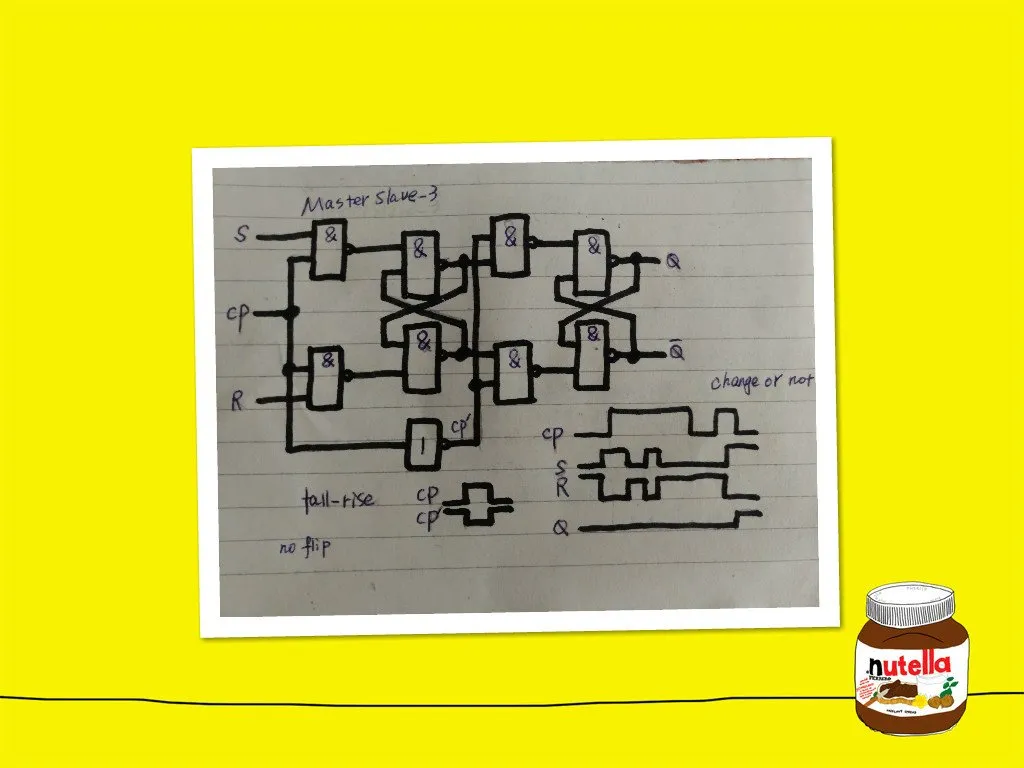
上图是由两个钟控触发器级联而成,称为主从RS触发器,前面连接输入信号的称为主触发器,后面连接输出信号的称为从触发器。主从触发器的时钟经过了一个反相器。
我们分析如下:当CP=1时,主触发器正常工作,从触发器被封锁,所以整个触发器的输出不变。当CP=0时,主触发器被封锁,从触发器工作,因为主触发器的状态不变,所以从触发器的状态也不会发生变化。所以不论CP等于0还是1,整个触发器始终为保持状态。
那么什么时候变呢?在CP由1变为0的那一瞬间,也就是CP的下降沿,输出发生变化,我们称这类的触发器为边沿触发器。如果为上升沿触发一般称为正边沿触发器,如果下降沿触发,一般称为负边沿触发器(但其实这仍属于脉冲触发器,因为主触发器的状态是在CP为高电平时获取的,严格的边沿触发器是状态的更新或获取都是在边沿到来时发生的)。我们可以根据图中的波形图来分析一下这个触发器的特点。当CP=0时,假设输出Q一开始为低电平,因为CP=0的时候,主触发器被封锁,其值不变,从触发器的值也会保持不变(即使R和S发生了变化)。当CP跳向正电平时,主触发器被打开,从触发器被封锁,从触发器仍输出刚才的低电平。主触发器随着S和R的变化而变化,它的输出由高电平变为低电平又变为高电平又变为低电平,此时CP由高电平变为低电平(产生了一个下降沿),主触发器被锁定为刚才的低电平,从触发器被打开,更新为此时的低电平。然后CP又产生一个上升沿,主触发器打开,从触发器被锁存,仍维持原来的低电平,然后主触发器的输出随着S和R的变化由低电平变为高电平。最后时钟又产生一个下降沿,主触发器被锁定为高电平,从触发器打开,输出更新为高电平。由这个分析结果可知,主从触发器解决了空翻问题,即一个时钟周期无论S和R怎么翻转,输出最多翻转一次。但这个触发器在CP=1的时候,S和R仍然不能同时为1。输入有限制让我们感觉到不舒服,我们想再改进一次,以改变这种限制,于是有了主从JK触发器,如下图所示。
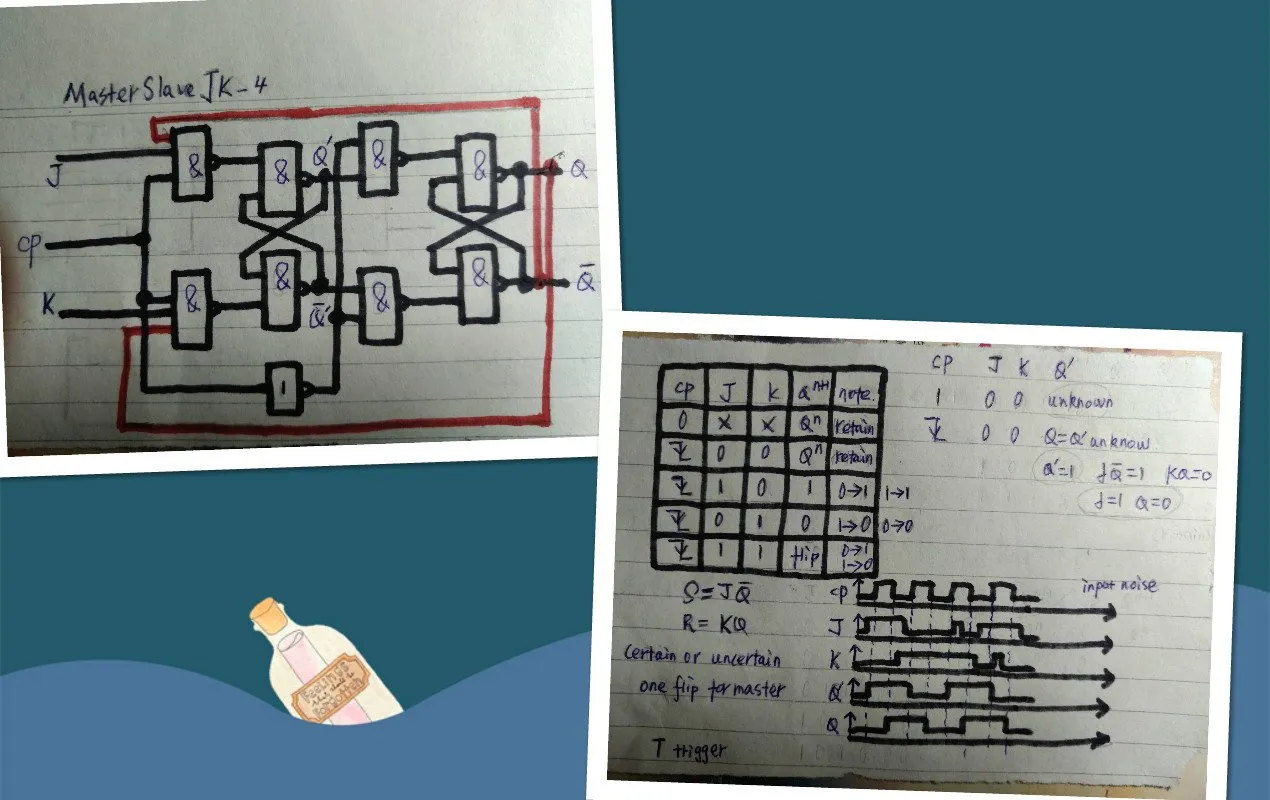
由上图的左上边的图可以看出主从JK触发器是由主从RS触发器外加两条反馈线构成的。因为Q和Q是互补的,所以任何时候都会有一个门被锁定,所以就不用担心J和K同时为1了。这样,原来的R、S触发器的S=J(Q),R=KQ(如上图的右下角所示)。
那么我们首先来分析一下图中的特性表。CP=0时,主触发器被锁定,维持原来的值,从触发器被打开,由于主触发器不变,所以从触发器也不变。CP=1时,主触发器打开,从触发器被锁存,所以触发器的得输出也仍保持原来的值,但此时主触发器的输出会受到J和K以及输出Q,~Q的影响。如果在CP下降沿期间,J和K均为0,则主触发器下降沿之前就被锁存了,下降沿的时刻,主触发器仍被锁存,从触发器被打开,并将主触发器的输出作为输入进行更新,但主触发器被锁存的值,我们不知道,所以更新后的值也无法分析,所以我们需要往前推导,从我们已知的地方进行分析。因为J=0,K=0,所以触发器一直被封锁,一直保持在从触发器更新后的状态,所以如果此时CP产生一个下降沿,触发器的输出仍会保持不变。下面我们来分析其余三种情况。
假设CP等于1的时候,J=1,K=0,Q=0,所以此时主触发器输出Q'=1,那么CP在下降沿的时候,从触发器的输出Q更新为1;假设Q原先就等于1,那么主触发器在上一次从触发器更新后就一直被封锁,从触发器输出Q为1,说明主触发器被锁存的值肯定也为1,所以如果J=1,K=0,触发器输出为1。那么如果CP=1的时候,J=0,K=1,Q=0,说明主触发器在上一次从触发器被更新后就一直被封锁,从触发器输出为0,那么主触发器被锁存的值也一定为0;如果Q=1,那么主触发器Q'=0,CP在下降沿时候,从触发器就会被更新为0,所以J=0,K=1,触发器输出为0。还有一种情况,就是CP=1时,J和K都等于1的情况,假设Q等于0,则Q'=1,CP在下降延时刻Q被更新为1;假设Q=1,则Q'=0,在CP下降延时刻,Q就会被更新为0,所以J=1,K=1会使触发器的输出翻转。
但是这个电路有一个问题,我们可以通过分析图中的波形图来分析这个问题。CP=0时刻,J=0,K=0,假设Q'和Q初始状态都为0,那么J=0,K=0使主触发器处于锁存状态,保持当前的状态Q'=0,然后J变为1,CP=0使主触发器仍为封锁状态,Q'和Q保持不变。然后CP变为高电平,J=1,K=0,Q=0,所以~Q=1,Q'=1,然后CP变为低电平,主触发器被封锁,从触发器打开,Q被更新为1,然后CP又变为高电平,J=0,K=1,Q=1,得出Q'=0,在CP又变为低电平时,Q更新为0,然后CP又变为高电平(还可以分析J从0->1->0),J=1,K=1,Q=0,则Q'=1保持不变,然后问题来了,此时J又变成了0,K仍等于1,Q=0,Q'仍保持原来的值,咦,不是J=0,K=1输出置0么?可见Q'由于反馈的作用没有对这种变化做出反应。我们继续分析,然后CP产生了一个下降沿,Q被更新为高电平。然后CP又变为高电平(还可以分析K从0->1->0),此时J=1,K=1,Q=1,则Q'变为0,若果K又变为了0,则Q'不变,咦,不是应置1么?可见Q'也没有对K的变化作出响应。如果这个小脉冲是一个干扰噪音,输出仅仅对这个噪音的脉冲做出了反应,却没有对后续的恢复做出反应,这是一个很严重的问题,称为“一次变化的现象”,即CP为高期间,J和K的任何变化会使主触发器发生一次变化(不会是多次),从而将变化输出到Q上。
所以为了解决这个问题,我们又创作出了边沿触发器,比如边沿JK触发器和边沿D触发器,不过限于篇幅原因,这里就不在多说了,我将在另一篇文章中再行说明。
说明:文中图片皆为作者手绘后拍照在进行设计美化。
参考资料: