La publicación pasada estuvimos abordando el tema de la asociación de resistores en serie, en ésta ocasión desarrollaremos lo que es la conexión de resistencias en paralelo, así como también presentaremos algunos ejemplos prácticos sobre ambas asociaciones.
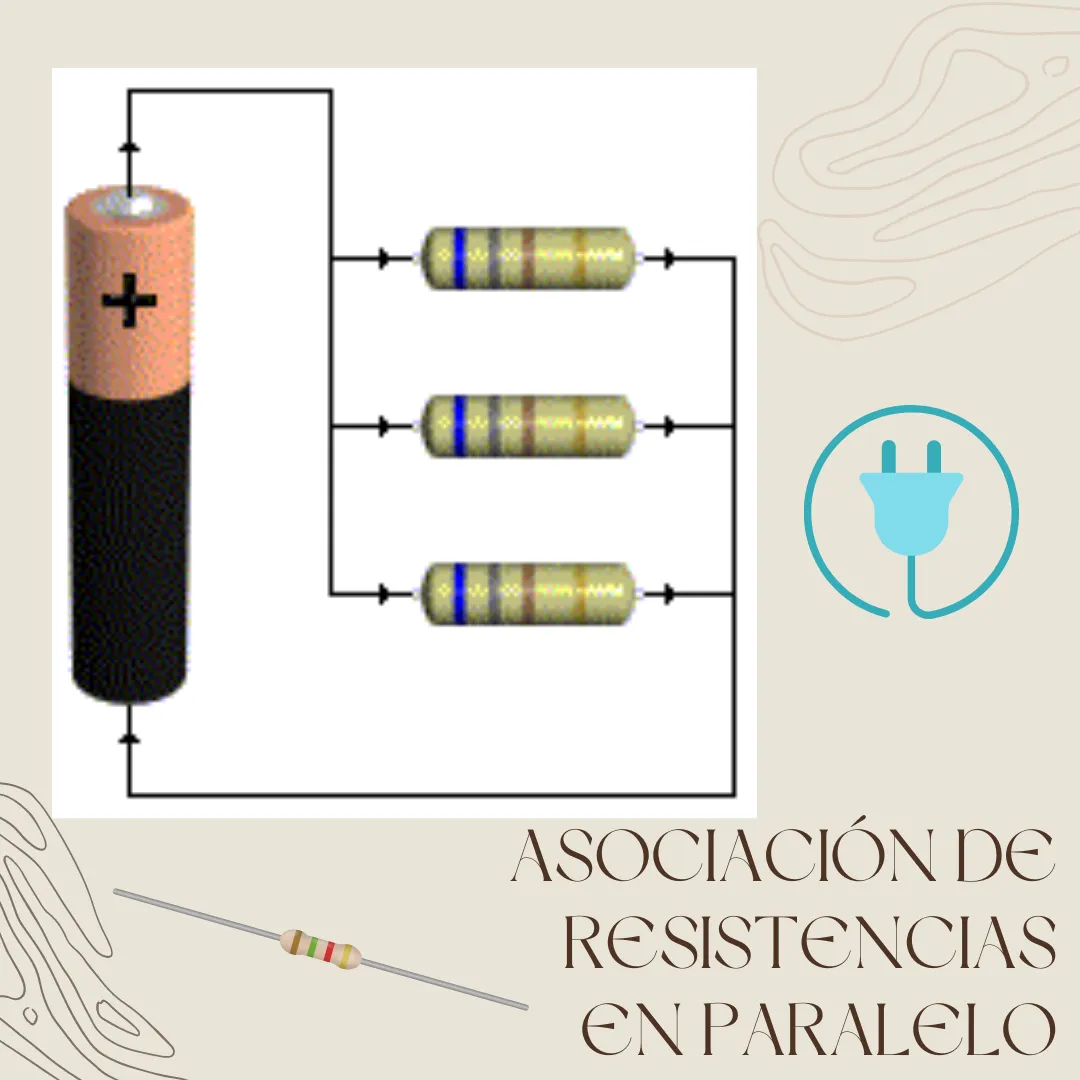
Imagen realizada con la página web de diseño gráfico y composición de imágenes Canva.
Si recordamos un poco lo que estudiamos en la publicación pasada, sabemos que cuando dos o más resistores se encuentran conectados en serie es porque se posicionan uno seguido del otro. Por otra parte, tenemos una segunda manera de conectar las resistencias y esto es mediante una asociación en paralelo. Cuando dos o más resistencias se encuentran asociadas en paralelo, es porque su conexión está unida de sus extremos, es decir, cada resistencia forma parte de una rama diferente que a su vez divide el circuito, tal como se muestra en la imagen a continuación.
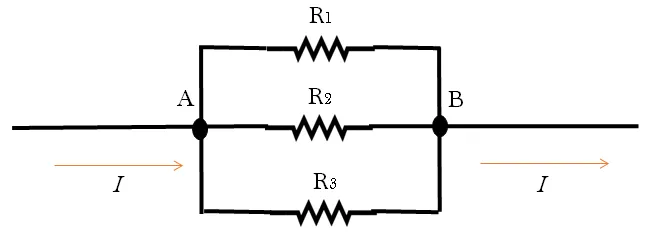
Ahora bien, es importante acotar que cuando existe una conexión en paralelo la intensidad de corriente eléctrica que atraviesa por cada resistor no resulta ser necesariamente la misma, pero por otra parte, la diferencia de potencial entre los extremos de cada resistencia deben ser las mismas e iguales a Vab. Es importante acotar que la diferencia de potencial entre cualquier punto, no depende del camino seguido entre dichos puntos. Si tenemos las siguientes corrientes I1, I2 y I3, y I = V/R
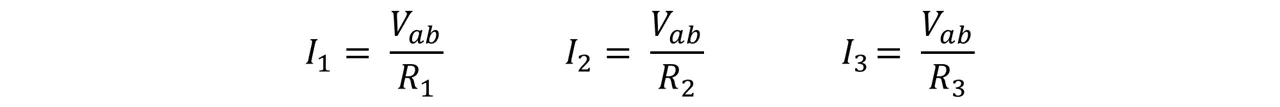
En líneas generales, la corriente es diferente en cada resistencia, ya que no se pierde, ni se acumula carga por el punto a, es por ello que la corriente total debe ser igual a las tres corrientes individuales.
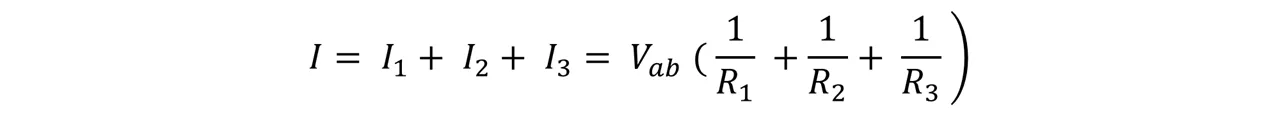
Si extraemos Vab al primer miembro de la ecuación nos queda que:
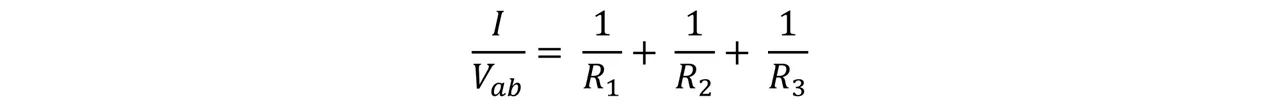
Como por definición tenemos que
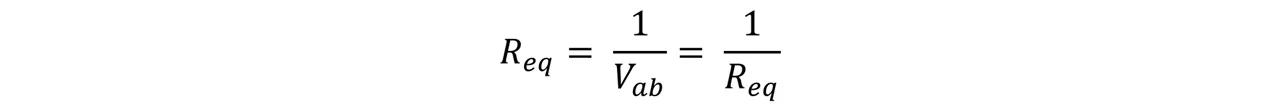
Por lo tanto,
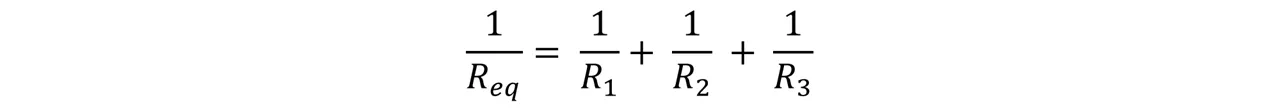
Es oportuno resaltar que esta expresión es simple para generalizarla a cualquier número de resistencias en paralelo:

Y partiendo de ésta expresión podemos resaltar la definición según Zemansky (2009) de una asociación de resistencias en serie como:
En el caso de cualquier número de resistores en paralelo, el recíproco de la resistencia equivalente es igual a la suma de los recíprocos de sus resistencias individuales.
Sabiendo también, que la resistencia equivalente siempre es menor que cualquiera de las resistencias individuales.
Si analizamos el resultado obtenido con el de la capacitancia equivalente de una asociación de capacitores en paralelo, podemos ver que los resistores conectados en paralelo se suman de manera recíproca ya que la corriente en cada uno de ellos es proporcional al voltaje común entre sus extremos y también es inversamente proporcional a la resistencia de cada uno. En los capacitores en paralelo se suman directamente porque la carga de cada capacitor es proporcional al voltaje entre sus bornes y es directamente proporcional a la capacitancia individual.

Ahora veamos desde el punto de vista práctico lo que hemos desarrollado. Supongamos que tenemos dos resistores, si se conectan en paralelo un resistor de 32 Ω y uno de 20 Ω, y se conecta la combinación entre los bornes una línea de corriente continúa de 240 V. ¿Cuál es la resistencia de la combinación en paralelo? ¿Cuál es la corriente total a través de la combinación en paralelo? ¿Cuál es la corriente a través de cada resistor?.
Éste es un ejemplo muy sencillo, consta de dos resistores que se encuentran conectados en paralelo y del cual primeramente nos piden calcular la resistencia equivalente. Sabiendo que la resistencia de dos resistores conectados en paralelo es:
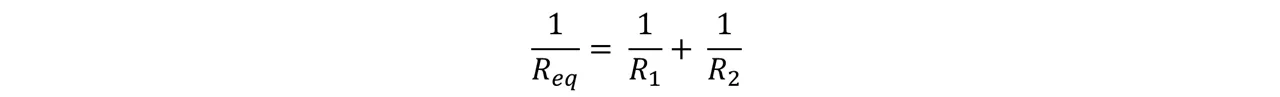
Si sustituimos los valores de los resistores tenemos que:
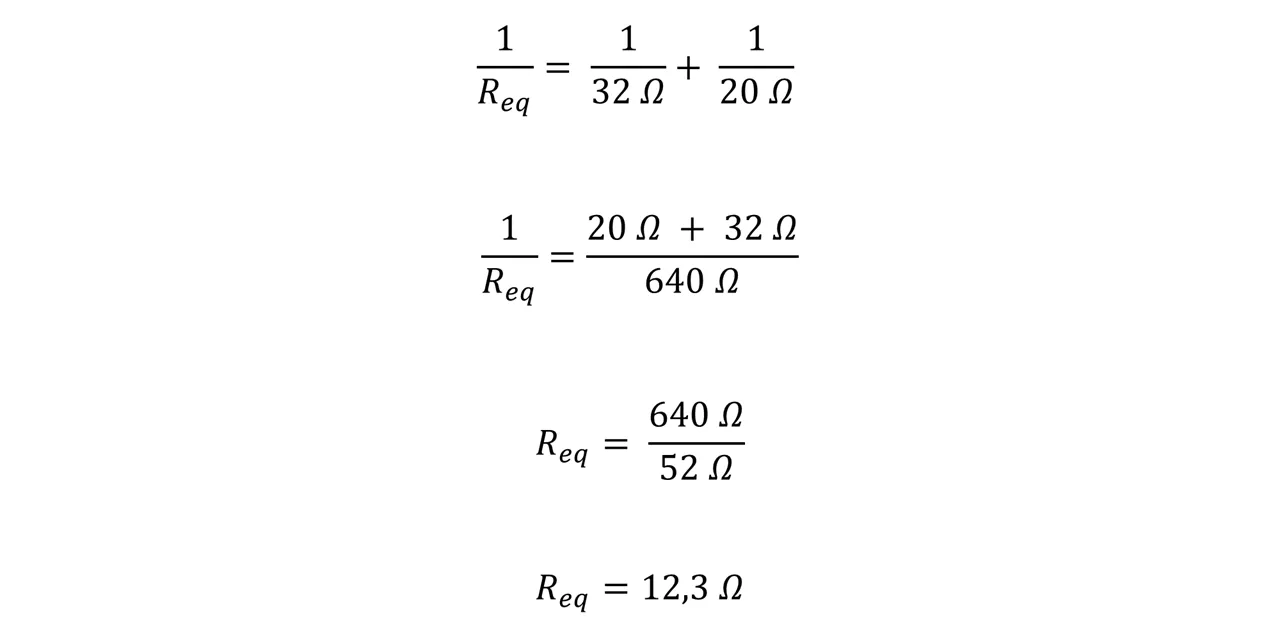
Una vez tengamos la resistencia equivalente podemos pasar a responder la segunda interrogante, la cual nos pregunta sobre la corriente total a través de toda la asociación. Para ello utilizaremos la siguiente expresión:
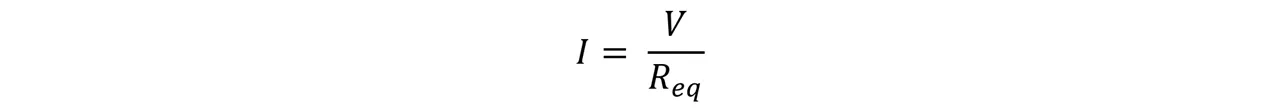
Sustituimos y nos queda:
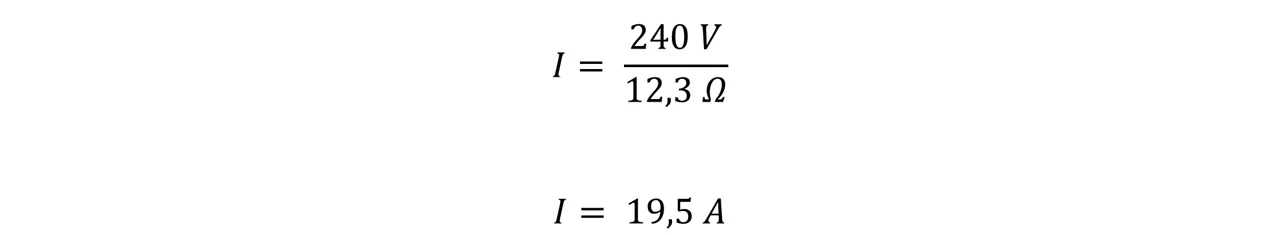
Ahora podemos responder la última pregunta la cual nos pide determinar la corriente través de cada resistor, para ello utilizaremos las resistencias individuales.
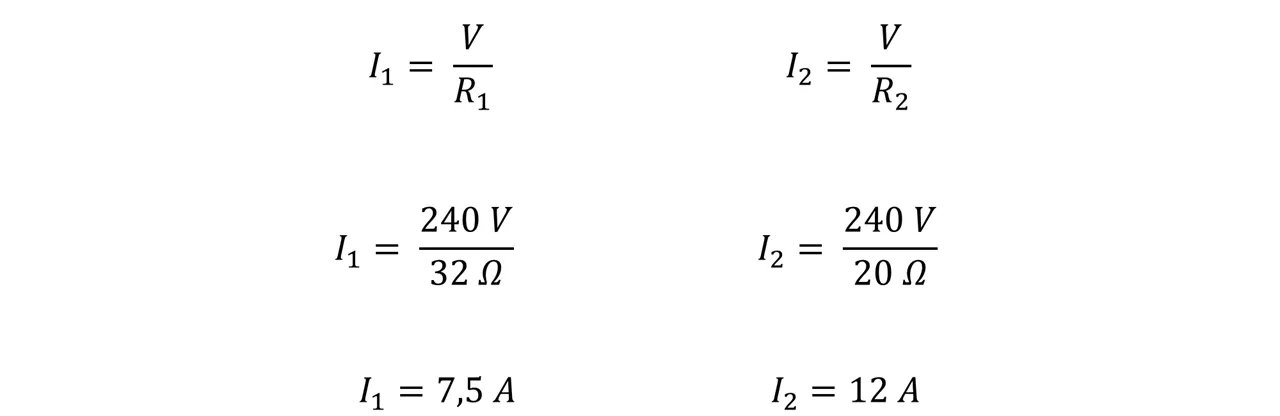
Finalmente podemos concluir que en una asociación de dos resistores en serie, cuyas resistencias sean 32Ω y 20Ω su resistencia equivalente será de 12,3Ω, por otra parte la corriente que circula por toda la combinación es de 19,5 A, mientras que la que pasa por el resistor 1 es de 7,5 A y por el 2 de 12A. De la cual podemos apreciar que donde la resistencia es mayor, menor es la corriente y viceversa.

Ahora veamos el segundo ejemplo el cual dice de la siguiente manera: Tres resistores con resistencias de 1,60Ω; 2,40Ω y 4,80Ω se conectan en serie a una batería de 28V cuya resistencia interna es insignificante. Hallemos: a) la resistencia equivalente de la asociación; b) la corriente en cada resistor, c) la corriente total a través de la batería; d) el voltaje entre los extremos de cada resistor.
En este ejemplo podemos observar que se trata de una asociación en serie, caso contrario al ejemplo que estudiamos anteriormente, lo primero que nos piden determinar es la resistencia equivalente, lo cual haremos mediante la siguiente ecuación:
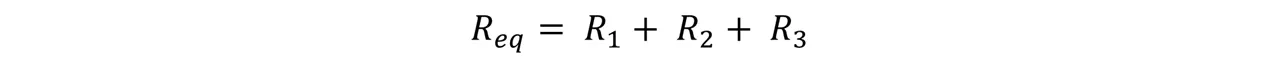
Sustituimos
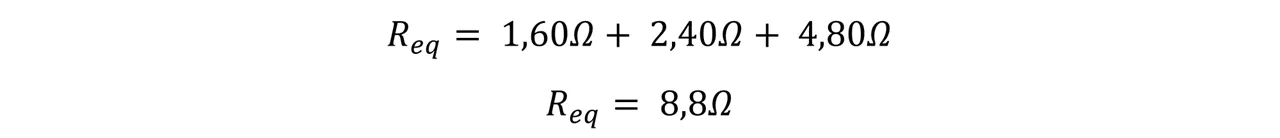
Como ya tenemos la resistencia equivalente, ahora podemos proceder a responder la pregunta dos, la corriente en cada resistor. Pero la corriente es la misma en cada resistor por lo que:
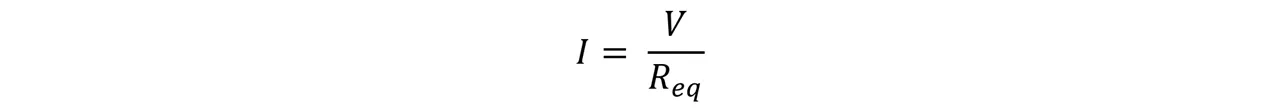
Sustituimos y nos queda:
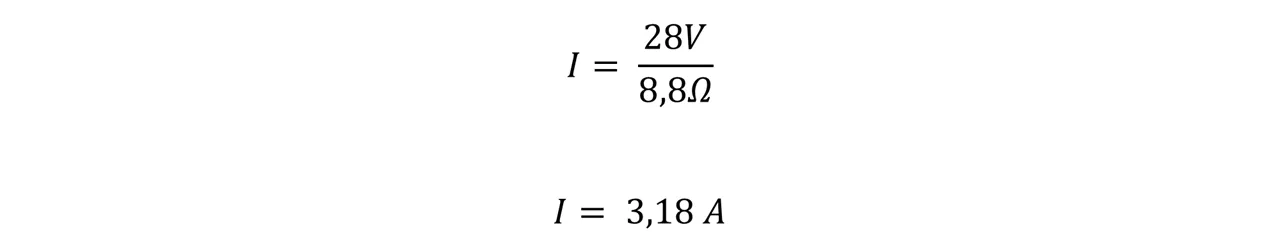
Una vez calculada la corriente en cada resistor, podemos responder la pregunta número que tres, donde nos piden hallar la corriente total a través de la batería, pero en un circuito en serie la corriente es la misma en toda la asociación, por lo que la corriente de la batería es 3,18A.
La última pregunta de este problema nos pide hallar el voltaje en cada extremo de los resistores, para ello utilizaremos las siguientes expresiones:
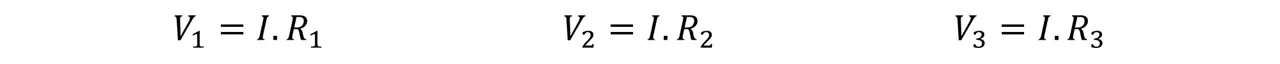
Sustituimos y obtenemos que:
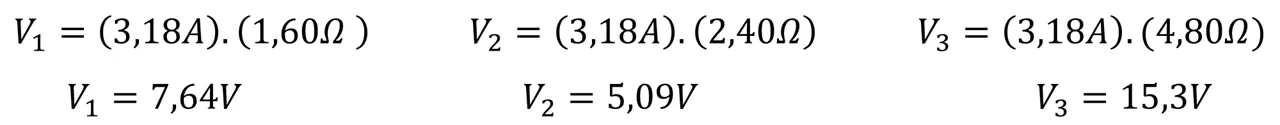
Ya para concluir podemos decir que para un circuito de tres resistores en serie, la resistencia equivalente que es la suma de cada resistencia individual es igual a 8,8Ω; mientras que la corriente de cada resistor y la que pasa por la batería es la misma y tiene un valor de 3,18A, pero los voltajes de cada resistor son diferentes y los mismos son 7,64V para el primer resistor, 5,09 para el segundo resistor y 15,3Vpara el ultimo resistor.

El tercer y último problema, consta de una combinación serie y paralelo. Calcule la resistencia equivalente de la red que se muestra en la imagen a continuación y encuentre la corriente total. Consideremos que la resistencia interna de la batería es insignificante.
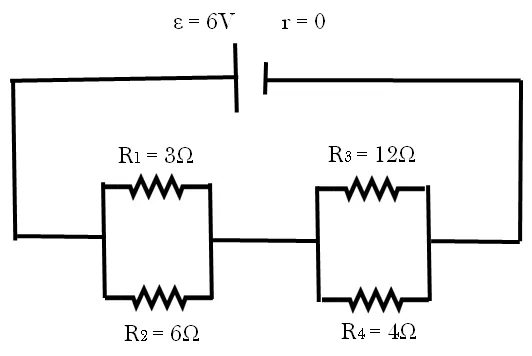
Lo primero que vamos hacer en este problema es determinar la resistencia equivalente, para ello comenzaremos primero las resistencias uno y dos que se encuentran en paralelo.
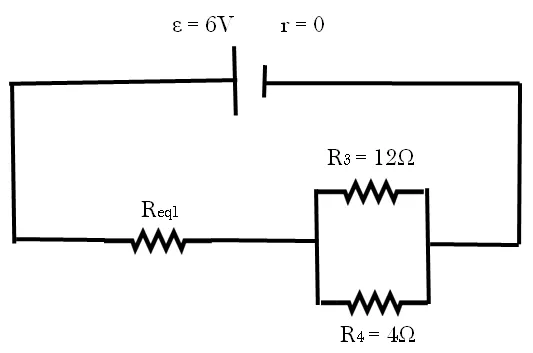
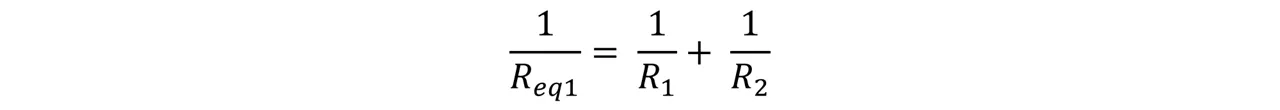
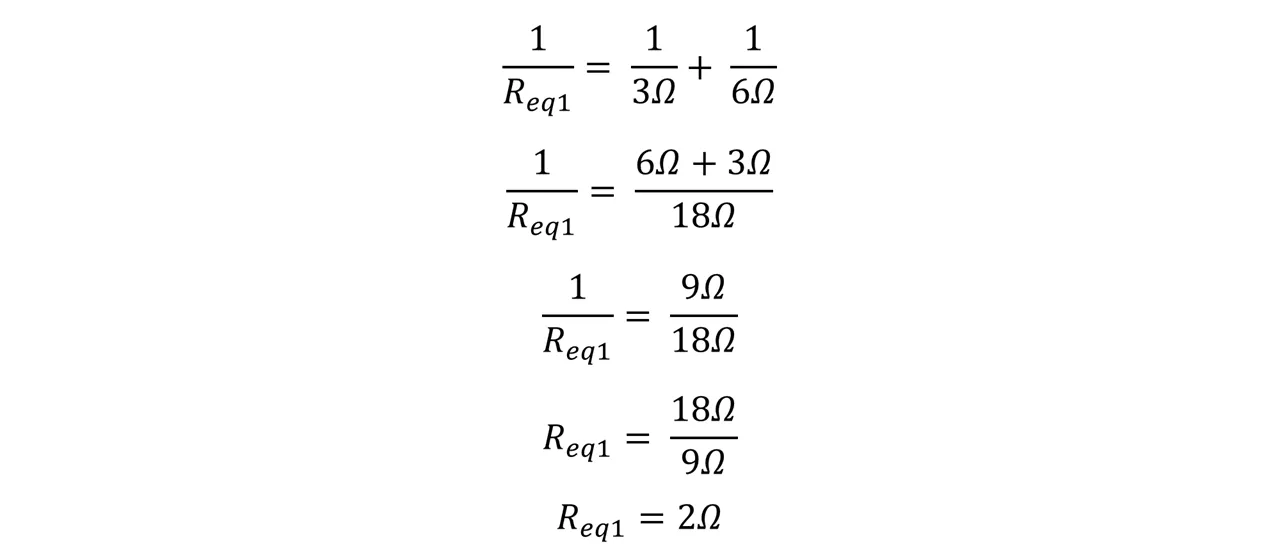
Luego buscamos la resistencia equivalente entre los resistores tres y cuatro.
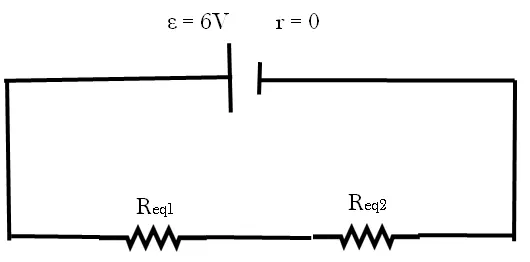
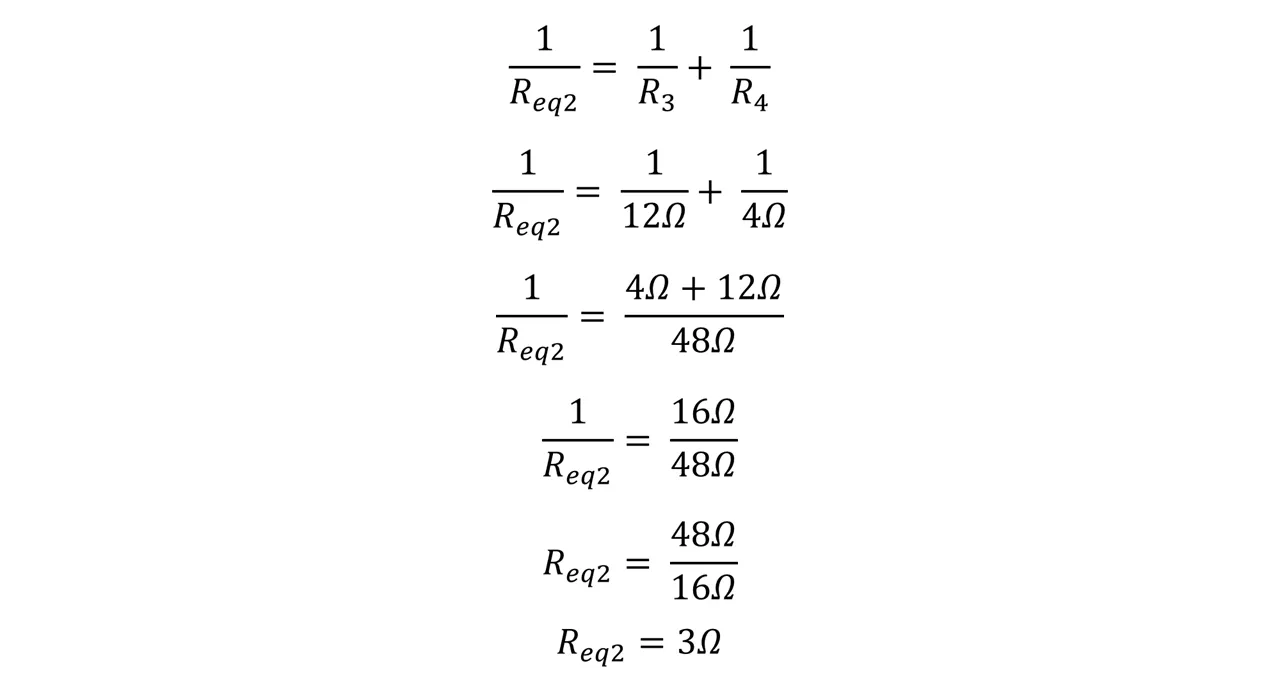
Como esas resistencias ahora quedaron en serie procedemos a sumar ambos resultados para obtener la resistencia equivalente total.
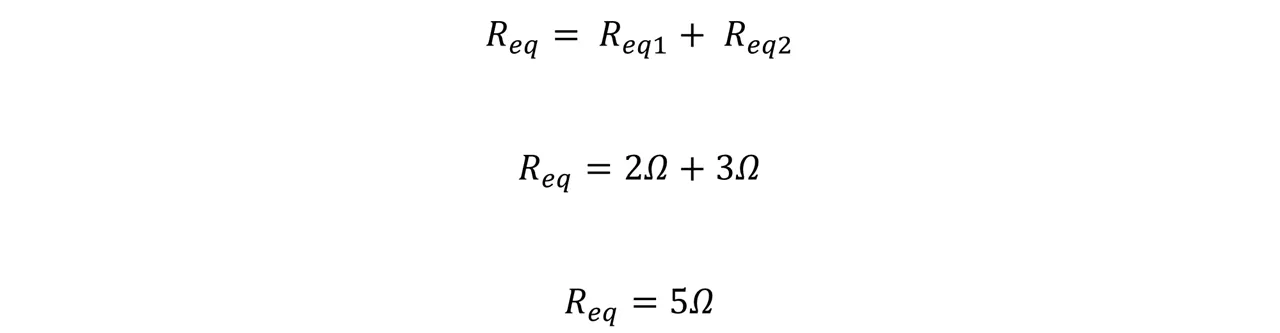
Ahora para continuar determinando la corriente en cada resistor debemos calcular I total.
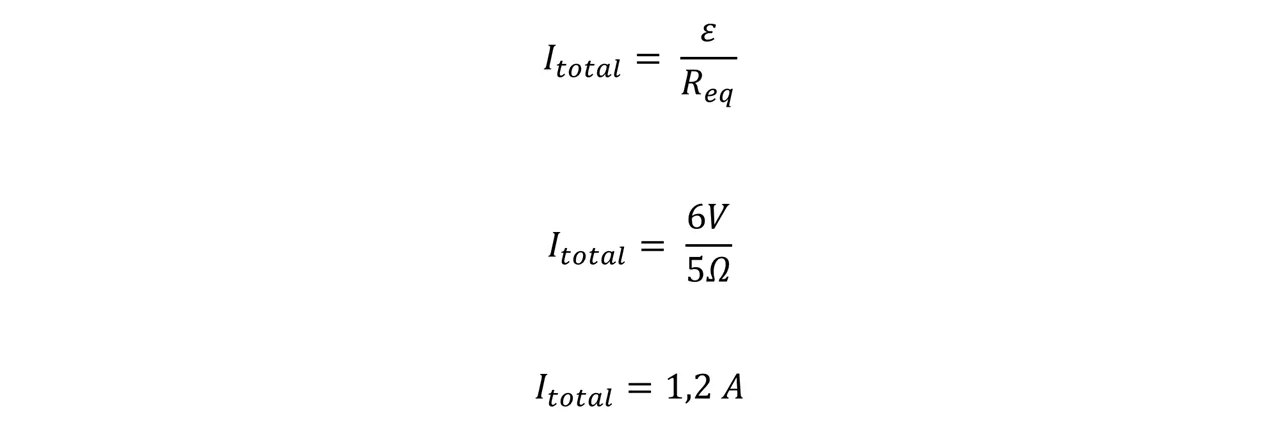
Finalmente podemos concluir que atendiendo a las diferentes formas en que se encontraban conectados los resistores la resistencia equivalente del circuito es de 5Ω y que I total es igual a 1,2A. Pero es importante tener en cuenta que ésta no es la corriente de cada resistor.

Referencias
Figuera, J. (2009). Física, Texto y problemario. Caracas: Ediciones CO-BO.
Sánchez, E. (2005). Física. Caracas: Ediciones CO-BO.
Zemansky, S. (2009). Física Universitaria Volumen II. México: Pearson Educación.

