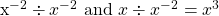Hi there. In this math post, I cover the topic of common factoring.
As usual math images are rendered in LaTeX with Quicklatex.com.
Topics
- Review Of Distributive Law
- Review Of Greatest Common Factors
- Common Factoring
- More Technical Cases
Review Of Distributive Law
Before getting into common factoring I do think it is a good idea to review distributive law from algebra and greatest common factors (GCF).
The distribute law algebra technique deals with a single term multiplied by a binomial or polynomial. Here are some examples.
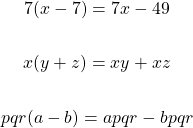
In all of these distributive law cases we multiply the left side not in brackets by every term in the bracket. The result is a sum of products. Do watch out for negatives when applying the distributive law.

Review Of Greatest Common Factors
Think of number factors as numbers that are used for multiplication. Factors of 10 are 1, 2, 5 and 10. This is because we have 1 x 10 = 10, and 2 x 5 = 10 and the other way around.
A common factor is a factor that is a factor in two different numbers. Common factors for 5 and 10 are 1 and 5.
Factors of 5: 1 and 5
Factors of 10: 1, 2, 5, 10
Common Factors: 1 and 5
The greatest common factor (GCF) is just the largest common factor between two numbers. For 5 and 10, the greatest common factor is 5.
GCF With Variables
Finding the greatest common factor with variables gets a bit more tricky. Consider finding the GCF for x and x cubed.
- Factors of x: 1, x
- Factors of x-cubed: 1, x, x-squared, x-cubed
- Common Factors: 1 & x
The greatest common factor here is just x.
Common Factoring
Common factoring from algebra builds upon the knowledge of greatest common factors. The reverse of the distributive law is common factoring.
Example One
Factor  .
.
Factors of x-squared are x-squared itself, x and 1. For 3x the factors are 1, 3x itself, 3 and x. The greatest common factor here is x.
Place this x GCF on the outside of the bracket. Inside the bracket would be x from x-squared divided by the GCF of x minus 3 from 3x divided by x.

Example Two
Use common factoring for 
The greatest common factor is just the number 3 as all the terms are multiples of 3.
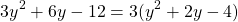
Example Three
Factor 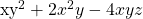
Be careful with this kind of case. If you need to start with greatest common factor as a number and then add the GCF in terms of variables.
Here the GCF here is 2xy. Every term has an even coefficient and has xy.


More Technical Cases
In this section I cover more technical cases that you may encounter.
Example One
Use factoring on 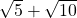
It is important to note that the square root of 10 is the square root of 5 times the square root of 2. The property of  is used.
is used.

The greatest common factor of the square root of 5 can be seen now.

The above factoring is usually not needed unless you need to simplify fractions with square roots. Factoring square roots can be useful.
Example Two
Factor 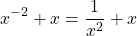
This case can be confusing. You may initially think that the GCF is just x. It is actually x to the power of negative 2. When you obtain the greatest common factor, you take the one with the smallest exponent.
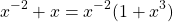
The 1 plus x-cubed is from