Saludos, bienvenidos a la Parte II de esta publicación, en la cual abordaremos el diagrama de fuerza cortante y sus bases matemáticas, donde podremos caracterizarlo por medio de ecuaciones que podemos encontrar de manera cuantitativa, a través del cálculo.

Como parte de este blog dedicado a la Estática Aplicada, asignatura introductoria al mundo de las Estructuras en el estudio de la Ingeniería Civil, nos encontramos abordando (y finalizando) el segundo tema referente a los diagramas de solicitaciones:
•Diagramas de fuerza axial (N).
•Diagramas de fuerza cortante (V).
•Diagramas de momento flector (Mf).
•Aplicaciones prácticas de los Diagramas de Solicitaciones.
•Metodología para elaborar los diagramas de solicitación ante cualquier sistema de cargas.
Introducción
Tal como lo he venido mencionando en publicaciones anteriores, las solicitaciones (cargas o fuerzas internas) en un sistema isostático, corresponden a las fuerzas internas que se generan como respuesta a la aplicación de cargas externas. Las características de las cargas externas serán las que determinen la manera en que “fluyen” o se comportan estas fuerzas internas o solicitaciones dentro de los distintos miembros del sistema.
En la Estática, resolvemos sistemas isostáticos, ya que el número de vinculaciones o restricciones (incógnitas) permiten la aplicación directa de las ecuaciones de equilibrio estático. En cambio, sistemas con mayor número de incógnitas que ecuaciones, necesitan de la aplicación de métodos adicionales para su resolución, los cuales escapan del área de la estática, y se estudian en cursos posteriores.
En cursos subsiguientes a “Estática Aplicada” se da paso a la resolución de estos sistemas con mayor número de incógnitas que ecuaciones (sistemas hiperestáticos), y más adelante, esto se sustituye por problemas en sistemas estructurales reales, como pórticos de edificios o estructuras de acero.
Sin embargo, la elaboración de los diagramas de solicitaciones siempre se basa en los mismos principios, sea un sistema isostático en el ámbito académico, o el sistema estructural de un edificio real. Por ello se entiende la importancia de aprender a elaborarlos con mayor efectividad antes de llegar a cursos posteriores, donde se asume que ya el estudiante sabe elaborarlos.
Aplicación del cálculo en los diagramas de solicitaciones |
Ya se había abordado esto en la publicación sobre las fuerzas axiales, pero en este caso intentaré profundizar un poco más en la teoría detrás del uso del cálculo para elaborar estos diagramas. La aplicación del cálculo se basa en que existen relaciones diferenciales e integrales entre las solicitaciones y las cargas externas.
Basándome en lo ilustrado y explicado por el Prof. Iván Rodríguez en su obra titulada “Estática de las Estructuras”, intentaré llevar a cabo este abordaje matemático de manera didáctica. En la siguiente imagen, podemos observar un elemento lineal horizontal “AB” (barra) sometido a una carga distribuida con la forma de una función cualquiera “q(x)” actuando en sentido positivo (hacia arriba).
Tendremos presente que:
-La carga distribuida en dirección del eje local cortante “V”, la cual podríamos llamar “qV(x)”, la llamaremos simplemente “q(x)”.
-Se obviará la representación de las fuerzas axiales y los momentos flectores, puesto que solo nos interesa estudiar la fuerza cortante.
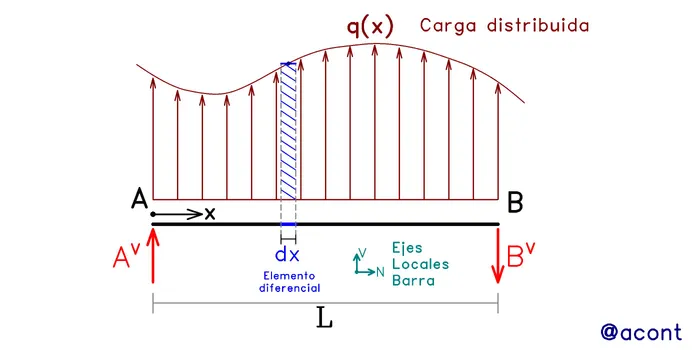
Existen reacciones verticales en sus extremos, las cuales se generan producto de la aplicación de la carga externa. Esto podría verse en cualquier elemento horizontal de un sistema isostático, o en una viga simplemente apoyada. Estas reacciones, al estar orientadas en dirección del eje local “V”, podría decirse que son fuerzas de corte actuando en los extremos.
Podemos observar en la Fig. N°1 que se ha resaltado un elemento diferencial “dx” del sistema. Si realizamos una especie de acercamiento o zoom a este elemento diferencial, nos encontraremos lo siguiente:

En el extremo izquierdo del elemento diferencial, observamos una fuerza de corte “V” actuando hacia arriba. Tenemos un segmento diferencial de la carga distribuida, cuya fuerza equivalente “F’” sería igual a su magnitud multiplicada por la longitud del elemento diferencial (q(x)∙dx).
Por otra parte, en el extremo derecho tenemos una fuerza de corte igual a “V+dV” actuando hacia abajo, ya que presenta una variación diferencial de su magnitud de un punto a otro que podemos llamar “dV”. La fuerza de corte en el extremo derecho se da de esta forma ya que esta es la magnitud y sentido necesarios para mantener el equilibrio estático en el elemento diferencial.
Seguidamente, procedemos a realizar una sumatoria de fuerzas en dirección del eje cortante “V”, el cual, en este caso, al ser la barra horizontal, coincide con la dirección vertical. Igualamos esta sumatoria a cero, puesto que estamos en presencia de equilibrio estático:

Simplificando esta expresión, obtenemos lo siguiente:

Hemos llegado a esta expresión, la cual según Rodríguez (2003) nos dice que la variación de la fuerza cortante es igual a la ordenada o magnitud de la fuerza transversal.
Pero ¿Cómo se interpreta esto? Podría decirse que la magnitud de la variación de la fuerza cortante de un punto a otro, es igual a la magnitud de la fuerza equivalente que existe entre esos dos puntos. Sin embargo, lo que más nos interesa es el valor de la fuerza de corte “V” y no su variación, por lo que vamos a integrar la expresión encontrada anteriormente:

Según Rodríguez (2003), tenemos que la ordenada (o magnitud) de la fuerza de corte, es igual al área de distribución de la carga transversal. Esto nos indica que la fuerza de corte se relaciona directamente con el área debajo de la curva que define a la carga distribuida “q(x)”.
Podemos ver que la fuerza de corte “V” estará en función de “x”, por lo que puede decirse que V=V(X). Evidentemente, el proceso de integrar la función “q(x)” arrojará una constante, y el valor de esta constante lo determinaremos más adelante.
Modelado matemático de las cargas externas: q(x)
El abordaje matemático anterior, no toma en cuenta a las cargas o fuerzas puntuales, ya que estas solamente causan discontinuidades en el diagrama de fuerzas cortantes.
Al igual que lo sucedido con las fuerzas axiales, las cargas distribuidas usualmente se representan de dos formas: uniformes (valor constante); o lineales (representadas por la ecuación de una recta). A esto podemos sumarle el hecho de que la carga distribuida también puede no existir, es decir, q(x)=0.

Podemos ver que se aplican los mismos principios que los utilizados para la elaboración de los diagramas de fuerza axial, solo que, en este caso, las cargas externas presentan una visualización un poco más evidente de las ecuaciones que las definen, en contraste con la carga distribuida axial, la cual se representa mediante flechas alineadas entre sí.
El valor de “a” y “b”, se obtiene mediante la evaluación de la ecuación al inicio y al final de la carga distribuida correspondiente. Para ilustrar esto de una manera más práctica, tenemos los siguientes ejemplos en la Figura N°4.
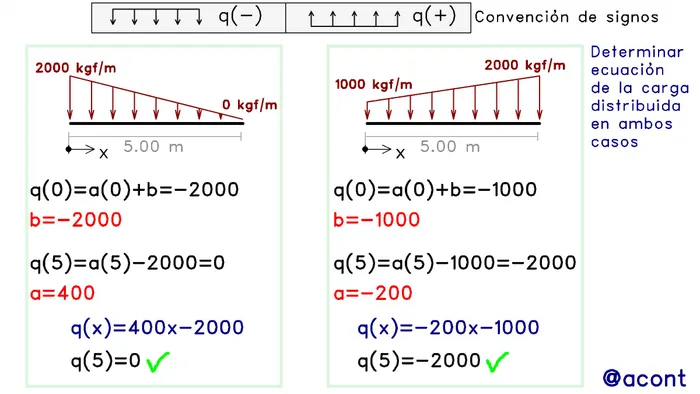
Si la carga distribuida se dirige hacia abajo, lo cual suele ser el caso frecuente, entonces el valor de “q(x)” es negativo, por ello al momento de evaluar esta función al inicio y al final, obtenemos ecuaciones igualadas a un término negativo, las cuales nos permiten despejar los valores de “a” y “b”.
Debo hacer hincapié en el hecho de que la ecuación q(x) no representa a la carga distribuida tal como se ve, sino a la carga distribuida en sus valores negativos o positivos. Esto se entiende mejor en la Fig. N°5:

Suele surgir mucha confusión a la hora de hallar los valores de “a” y “b”, ya que la ecuación hallada resulta tener una pendiente inversa a la forma observada de la carga distribuida, pero la forma correcta de comprobar esto es evaluando la ecuación encontrada para el punto inicial y el punto final, donde los valores a obtener deben coincidir en magnitud y signo con lo observado en la carga distribuida.
También es posible establecer ecuaciones con sus signos ya predeterminados para cada configuración de la carga distribuida trapezoidal (creciente, decreciente, hacia arriba o hacia abajo), donde solo hay que introducir los valores de la carga distribuida. En lo personal, recomiendo el método de evaluar “q(x)” para hallar los valores de “a” y “b”, ya que esto nos permite asegurarnos que los valores son los correctos de manera más efectiva, sin tener que memorizar cuatro ecuaciones alternativas.
Hallando la ecuación del diagrama de fuerzas cortantes: V(x)
Tal como se ha expresado anteriormente, para hallar la ecuación que define matemáticamente al diagrama de fuerzas cortantes, lo que haremos será integrar la ecuación de la carga distribuida.
Al ser una integral indefinida, el proceso de integración nos arroja una constante “C”. Para hallar el valor de esta constante, recurrimos al extremo inicial de la barra, es decir, el extremo izquierdo de la misma. Cuando x=0, tenemos que todos los términos de la ecuación V(x) se cancelan exceptuando la constante “C”. El valor de la fuerza cortante V(x) en el extremo izquierdo corresponde al valor de la reacción ya existente en ese punto, la cual es conocida previamente producto de la aplicación de las ecuaciones de equilibrio estático:

De esta manera, tenemos una ecuación con la cual podemos describir matemáticamente el diagrama de fuerzas cortantes.
Vamos ahora con ejemplos prácticos.
Ejemplo N°1
Veamos el siguiente sistema isostático simple constituido por dos barras. Se elaborará el diagrama de fuerza cortante solo de la primera barra.
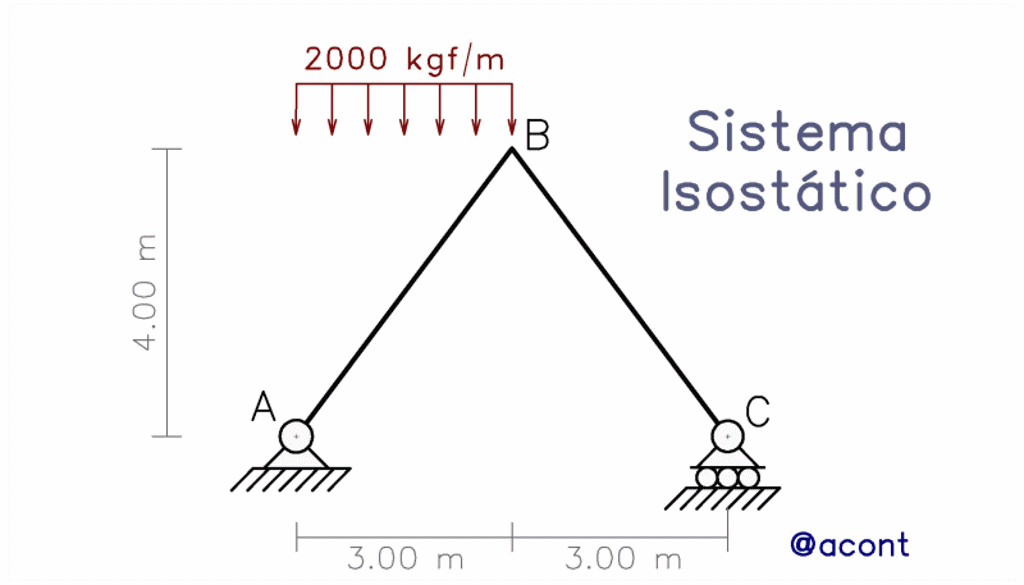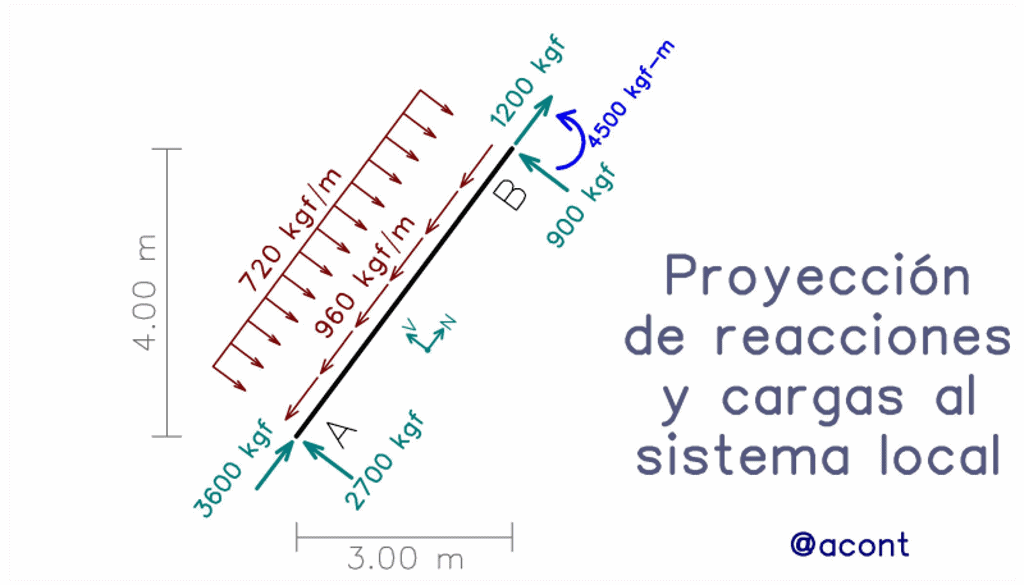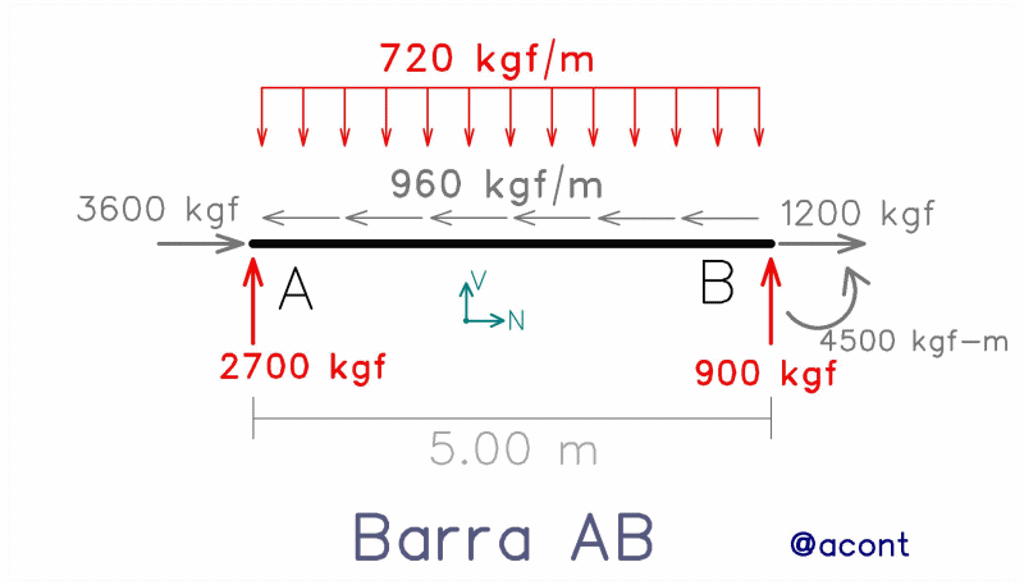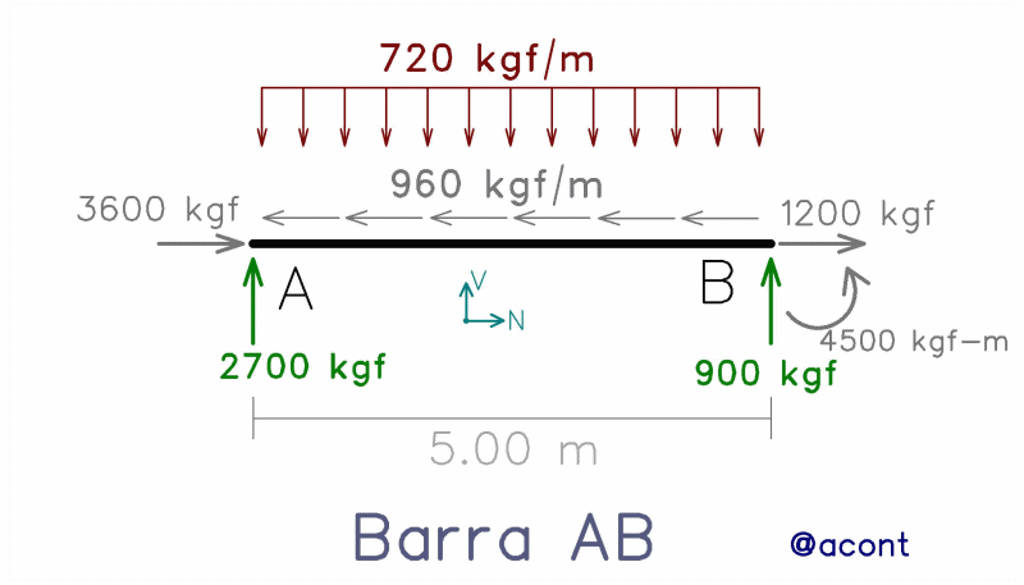
Tal como se observa, previamente a la elaboración del diagrama, se deben hallar las reacciones externas, realizar el despiece, y como la carga distribuida se encuentra en una dirección inclinada respecto al eje de la barra, fue necesario proyectarla al sistema de ejes locales de la barra. Dentro del material recomendado, podemos encontrar publicaciones dedicadas a estos procedimientos.
Cabe mencionar que, en problemas de la realidad, estos pasos previos a la elaboración del diagrama, suelen simplificarse en gran manera, ya sea por el uso de un programa de cálculo estructural o métodos aproximados para calcular directamente la fuerza de corte. No obstante, es importante que el estudiante adquiera sensibilidad respecto al cálculo que hay detrás y al resultado final, así como una buena noción de cómo las cargas externas influyen en las solicitaciones.
Volviendo al ejemplo, nos encontramos con una carga distribuida uniforme de 720 kgf/m dirigida hacia abajo. Esto nos permite formular la ecuación “q(x)” y posteriormente integrarla para obtener la ecuación del diagrama de corte “V(x)”:

Observamos que la constante “Vi”, es decir, el valor inicial, es conocida, pues es la fuerza de corte en el extremo izquierdo (2700 kgf). Su signo es positivo porque sigue la convención de signos para las fuerzas cortantes, donde la fuerza de corte en el extremo izquierdo del elemento es positiva hacia arriba. Esto nos permite graficar el diagrama (Fig. N°7).

Para comprobar que la ecuación hallada es correcta, evaluamos V(x) para x=5.00 m, esto nos arroja un valor negativo de -900 kgf, lo cual se valida, ya que observamos en el extremo derecho una fuerza de 900 kgf actuando hacia arriba. Según la convención de signos de esta solicitación, en el extremo derecho del elemento la fuerza cortante debe dirigirse hacia abajo para considerarse positiva.
Ejemplo N°2
Ahora abordaremos un caso con una carga trapezoidal (Fig. N°8):
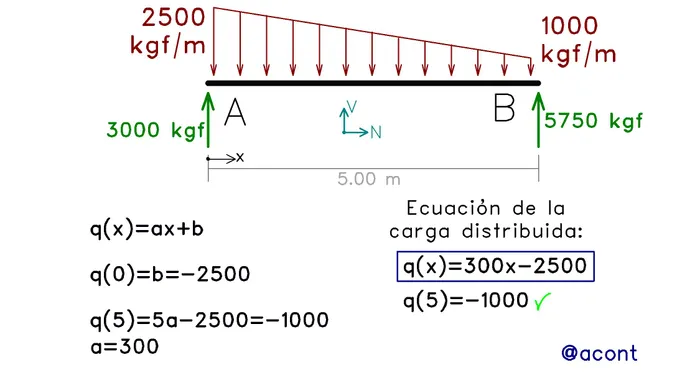
Al encontrar la ecuación que define a la carga distribuida, debemos verificar la misma. Si evaluamos q(0), esto nos arroja un valor de -2500. Si evaluamos q(5), esto nos arroja un valor de -1000, lo cual se valida al observar la carga.
Procedemos con la integración, lo cual nos arroja lo siguiente:

Conocido el valor inicial, procedemos a graficar esta parábola, mostrando así el comportamiento de la fuerza cortante dentro del elemento (Fig. N°9).

La ecuación encontrada nos permite caracterizar la forma del diagrama, si es una parábola que abre hacia arriba o hacia abajo, y si tiene o no puntos de corte en el dominio de interés. Si quisiéramos encontrar el punto exacto de corte con el eje del diagrama, es decir, donde V(x)=0, entonces debemos igualar la ecuación a 0 y despejar las dos soluciones de x:
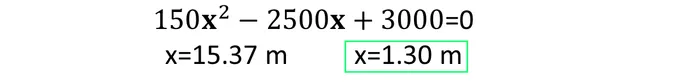
Las soluciones de x nos muestran que tenemos un punto donde V=0 a 1.30 m del extremo inicial, y otro punto que carece de interés práctico, ya que se sale de los límites del diagrama, pero nos muestra la ubicación del otro punto de corte con el eje en caso de extender la parábola fuera de los límites de interés.
Ejemplo N°3: discontinuidades, ejercicio de exámen.
Este ejemplo muestra una situación que suele ser un dolor de cabeza si no se logra identificar el error a la hora de abordar el ejercicio. Se trata de uno de esos detalles que pueden salir a la hora de un parcial. Veamos el siguiente caso, similar al anterior, solo que con una carga puntual actuando en conjunto con la carga trapezoidal (Fig. N°10).

Ya sabemos que la carga puntual nos introduce una discontinuidad en el diagrama. Sabemos que la ecuación de la fuerza de corte resulta de integrar la ecuación de la carga. Pero el detalle aquí es que la ecuación de la carga no es la misma antes y después de la carga puntual.
El error que se suele cometer es que se asume que la ecuación q(x) que representa a todo el trapecio es la misma a usar para ambos tramos (las discontinuidades nos dividen la barra en “tramos” o intervalos donde la ecuación de la carga puede cambiar).
El procedimiento correcto se expresa en la siguiente figura:

Se puede observar que el valor “b” de la ecuación de la carga distribuida cambia para el segundo tramo, es decir, la carga distribuida ya no está empezando en el valor del extremo izquierdo, sino en un valor intermedio, lo cual a su vez nos modifica la ecuación de corte V(x) para el segundo tramo.
Conclusiones y aportes
| Los diagramas de fuerza cortante nos muestran el comportamiento de una solicitación de suma importancia en el ámbito de la Ingeniería Civil, específicamente la ingeniería estructural. Se ha demostrado como la fuerza cortante depende directamente de las características de las cargas externas y cómo podemos emplear la matemática para caracterizar el diagrama. Se resume que el diagrama de corte puede ser constante, lineal o parabólico, dependiendo de si la carga distribuida es nula, uniforme o lineal respectivamente, es decir, se aumenta en un grado la ecuación matemática inicial. Esta publicación aporta un método para hallar la ecuación de la carga distribuida de una manera más eficiente, donde se puede entender el origen de los valores de “a” y “b” que posteriormente conforman la ecuación de la fuerza cortante. De esta manera se aporta material útil en el ámbito académico. |
Referencias Bibliográficas
[1]Rodríguez, Iván. (2003). Estática de las Estructuras. (p. 112-118).Fuente
Material recomendado
•Las Ecuaciones de Equilibrio Estático y algunas aplicaciones en la Ingeniería Civil
•Estática Aplicada: transformación de reacciones al sistema local en barras inclinadas
•Estática Aplicada | Proyección de cargas externas al sistema local de solicitaciones
•Estática Aplicada. Diagramas de Solicitaciones: Fuerza Axial Parte II
•Estática Aplicada. Diagramas de Solicitaciones: Fuerza Cortante Parte I
Imágenes y ecuaciones de autoría propia realizadas mediante LibreCAD y Microsoft PowerPoint. Gif creado mediante Photoscape.
Publicado mediante la dApp STEMsocial |
Visite la comunidad StemSocial y las etiquetas #STEMsocial y #STEM-espanol para encontrar contenido de calidad referente a Ciencias, Tecnología, Ingeniería, Matemáticas (STEM por sus siglas en inglés) y otros tópicos relacionados. STEMsocial es una comunidad con cuatro años de trayectoria conformada por autores de todo el mundo en la que se comparte y apoya la difusión de contenido STEM de calidad entre sus usuarios.
| Invitación al servidor de Discord de STEM-espanol: https://discord.gg/UJwQXWP | Registro en Hive |