Hello! math bugs(🐞) and hivers🐝)
I hope all is well.Thank you for your support.
Let's just head towards the subject.
In Geometry similarity is an easy topic but I have seen people to suffer when it comes with a right angle triangle and have a perpendicular drawn to hypotenuse from the opposite vertex as you have seen in cover photo.
Today I am here to make it lucid to you if you read me for a while.The figure below has three similiar triangle namely ∆ ABC , ∆ BDC and ∆ ADB. You may have noticed,I have mentioned the triangles in advancing order in area. Please take a look at the figure:⬇️
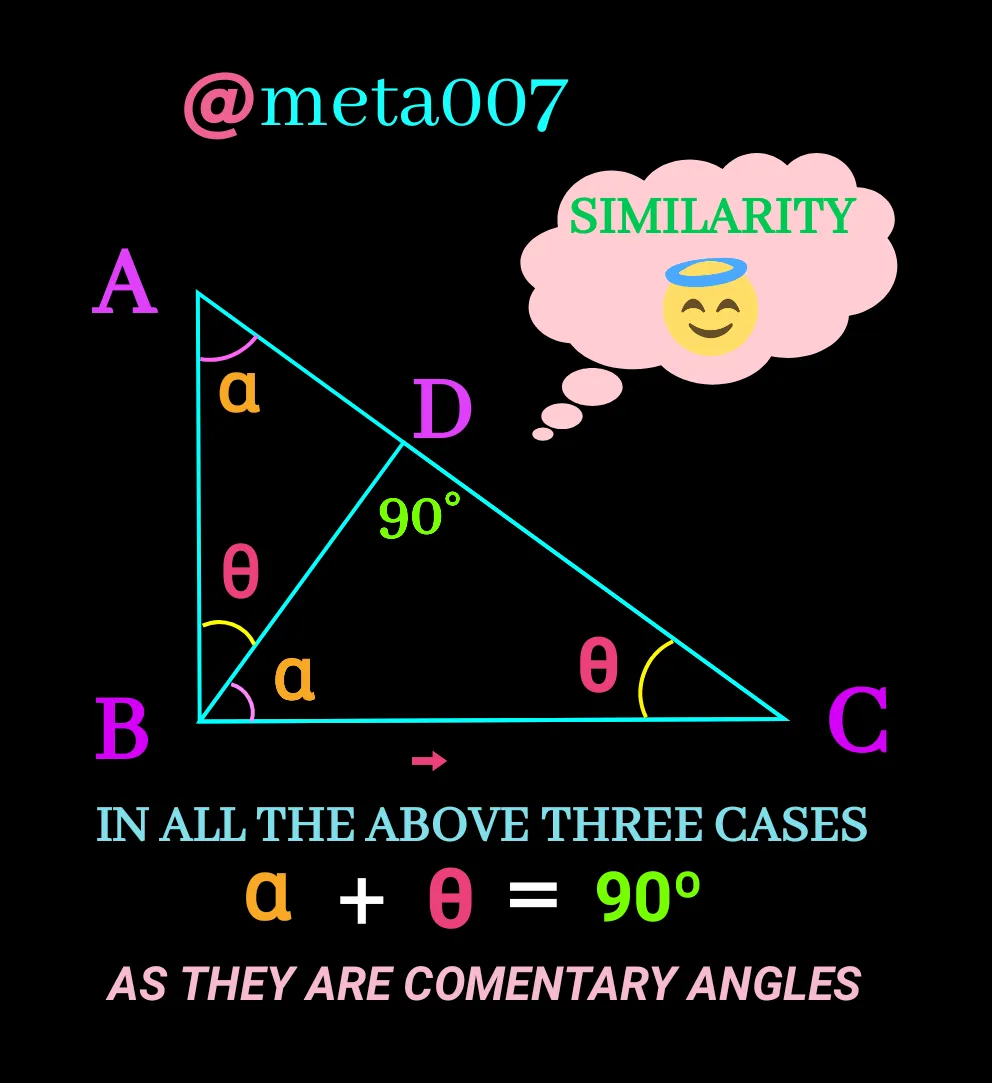
In above figure the triangles are combined together. let's make them separate in advancing order and naming them will also be in a order. I have named the ∆ ABC, ∆ BDC & ∆ ADB; you can't change order of the letters for one or two ∆ only .If you do, make it the same arrangement for every triangle accordingly. Check details:⬇️
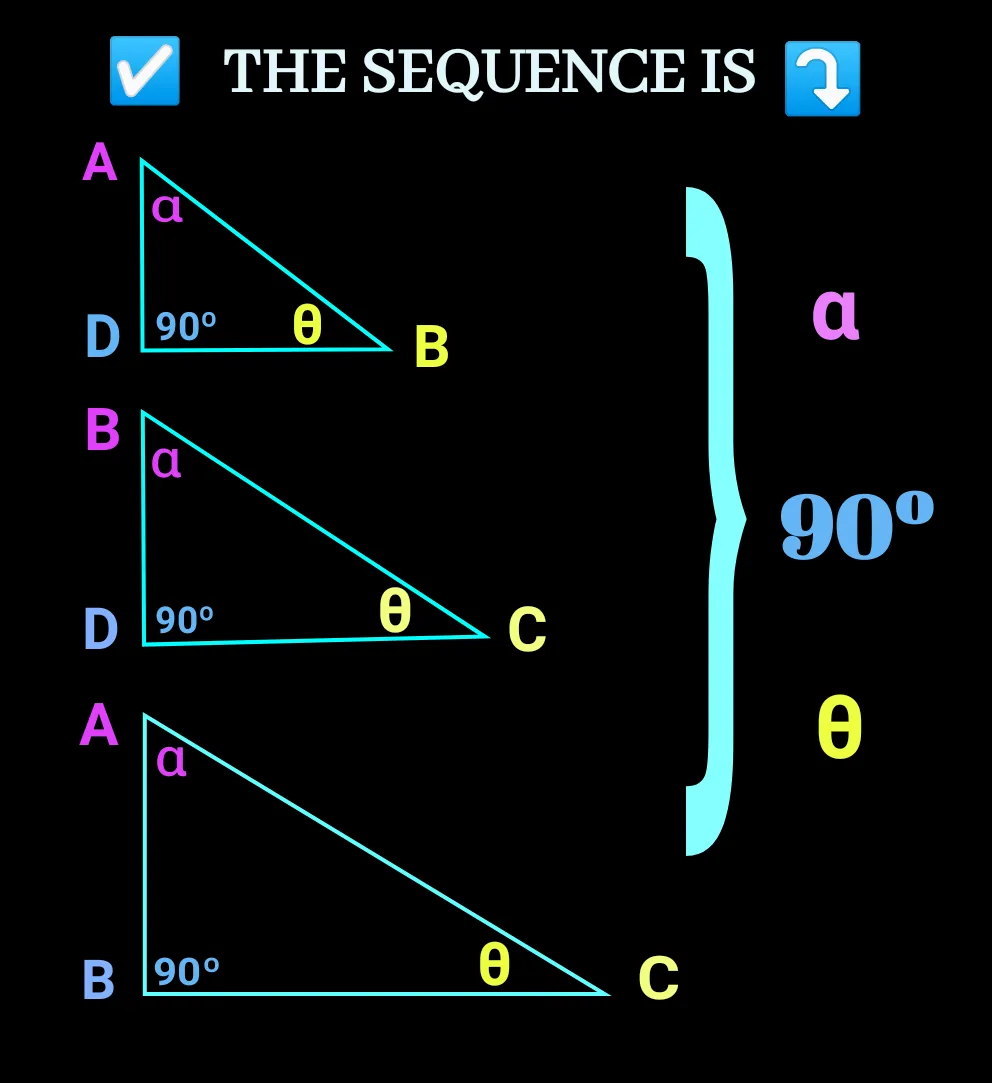
If you try to arrange the triangles like as shown in the above figure, it may cost you time. I have done it for your better understanding.The sequence of taking angles can be any but make sure they are the same for each triangle.let check how it can be done easily; how we can make the ratios instantly.
Confirm your sequence.
Let's go ascending order for now as my figures are based on it.
Small∆ > medium∆ > large ∆
RATIO: between angle & its opposite side.
Let's go: ⤵️⤵️

The above ratios are taken generally in case of trigonometry. If you are good at trigonometry, the problem won't arrive as I think but the other way we can represent it as follows :
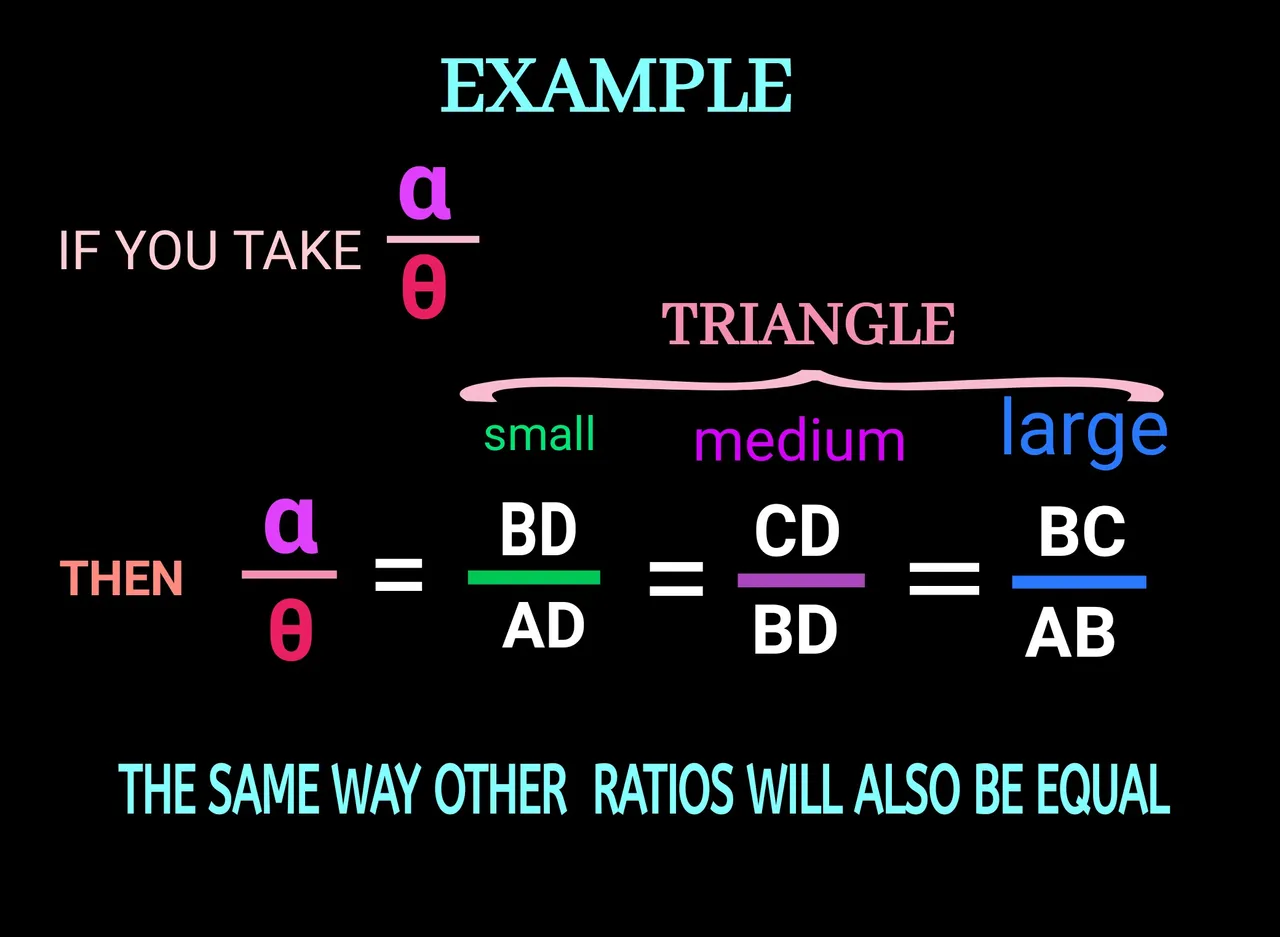
Ratio of any angle can be considered to form the ratios of sides as shown in the above figure.
You may think about what is going on. Let me face you a problem.If you try to solve the problem, you will get it if you go carefully trough what I tried to explain.Here is the problem:

Please feel free to make a comment.I shall be highly glad. I'm awaiting you.
I hope you have liked my post.
Thank you for stoping by.
Regards: @meta007
