| English | Español |
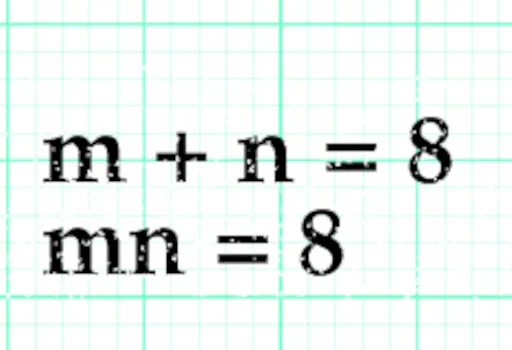
This problem shows a nice property, the equations are symmetric1 functions.
It's well know that the coefficients of a polynomial are symmetric functions of its own roots, so take the quadratic,
x² - (x1 + x2)x + (x1x2) = 0
We can transform our system of equations into a quadratic equation,
x² - 8x + 8 = 0
Solving, by completing the square,
x² - 8x = -8
x² - 8x + 16 = -8 + 16
x² - 8x + 16 = 8
(x - 4)² = 8
x - 4 = ± 2√2
x = 4 ± 2√2
x² - 8x + 16 = -8 + 16
x² - 8x + 16 = 8
(x - 4)² = 8
x - 4 = ± 2√2
x = 4 ± 2√2
whence,
m = 4 + 2√2
n = 4 - 2√2
m = 4 - 2√2
n = 4 + 2√2
the two solutions of the problem at hand.
1Symmetric function:
A function is symmetric if the exchange of its variables does not alters its value⤍| Español | English |
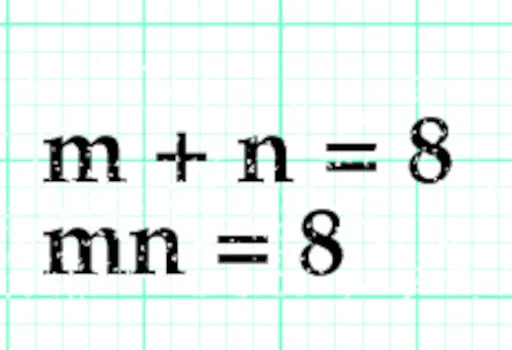
Este problema presenta una particularidad determinante, ya que las funciones que forman el sistema de ecuaciones lo son de un tipo muy especial, ya que son funciones simétricas1.
Es conocido que los coeficientes de un polinomio son funciones simétricas de las raices del mismo, así en el caso del polinomio de segundo grado,
x² - (x1 + x2)x + (x1x2) = 0
Podemos transformar el sistema de ecuaciones dado en una ecuación de segundo grado,
x² - 8x + 8 = 0
La resolvemos, por ejemplo, completando el cuadrado,
x² - 8x = -8
x² - 8x + 16 = -8 + 16
x² - 8x + 16 = 8
(x - 4)² = 8
x - 4 = ± 2√2
x = 4 ± 2√2
x² - 8x + 16 = -8 + 16
x² - 8x + 16 = 8
(x - 4)² = 8
x - 4 = ± 2√2
x = 4 ± 2√2
Por lo tanto,
m = 4 + 2√2
n = 4 - 2√2
m = 4 - 2√2
n = 4 + 2√2
son las dos soluciones del problema planteado.
1Función simétrica:
Una función es simétrica si intercambiando sus variables su valor no se ve alterado ⤍