Hi there. In this math post I cover the Mean Value Theorem or MVT for short.

Mean Value Theorem: Conditions and Formula
Let the function f(x) be continuous over the closed interval [a, b]. This function f(x) is also differentiable on the open interval (a, b). Then there is at least one point c ∈(a,b) (point c is in open interval (a, b)) such that
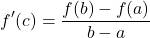
The right side of the equation is the slope of a line that passes through the points (a, f(a)) and (b, f(b)). Think of the slope equation from high school math.

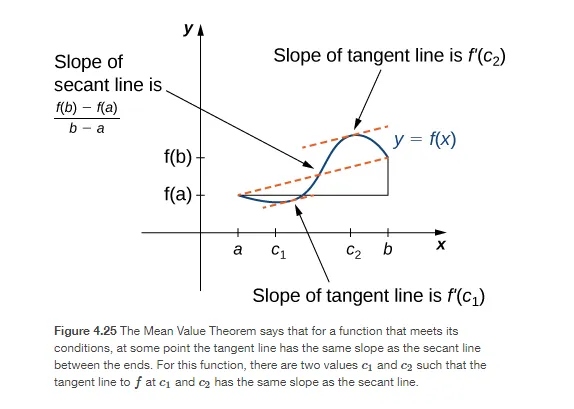
The left side of the Mean Value Theorem equation is the derivative of f(x) at the point c. The point c is an input value somewhere between the interval (a, b). This means that the slope of the line passing through (a, f(a)) and (b, f(b)) is the same value as the derivative at point c. Picture from openstax.org. shown below.
Different Formula
The Mean Value Theorem equation is:
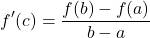
Sometimes you may seen the equation in a different form. This is because both sides are multiplied by (b - a).
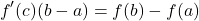
An Example
It is important to note that the Mean Value Theorem does not tell you what the value of c. The Theorem lets you know that there is a value c that satisfies the Mean Value Theorem equation seen above. You would have to have the value of c yourself.
Use the Mean Value Theorem where f(x) = 4x^2 - 1 on the interval [-1, 3] to determine all numbers `c in the interval (-1, 3).
The quadratic function is a continuous function on the interval [-1, 3]. This function is also differentiable on the open interval (-1, 3). The conditions for the Mean Value Theorem are satisfied.
With this question a = -1 and b = 3. The value of f(-1) is equal to 3 and the value of f(3) is equal to 35. Substitute these values into the slope part of the Mean Value Theorem.
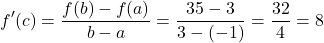
We now have f'(c) equal to 8. There is some value c such that the derivative at point c in the open interval (-1, 3) is equal to 8. Compute the derivative of f(x),
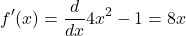
Set this derivative to the value of 8 computed earlier. Then solve of x.
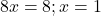
Check if this value of 1 is in the open interval (-1, 3). It is. The value of c is 1. The derivative of f(x) at x = 1 has the same value as the slope that passes through the points (-1, 3) and (3, 35). Desmos screenshot below. Note that that I have determined the equation of the line that passes through the points (-1, 3) and (3, 35). This line is 8x + 11.

Posted using STEMGeeks