Hi there. In this math post I cover the derivatives of exponential functions.
Math images rendered in LaTeX with QuickLatex.com.

Quick Review Of Exponential Functions
An exponential function has a number base to the power of an exponent that is a variable. One example of an exponential function is five to the power of x.
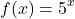
When x is equal to 1 you have the output f(x) equal to 5. With x equal to two you have five to the power of two which is 25. The input is the exponent.

Obtaining The Derivative Of Exponential Functions
The derivative of the exponential function is the slope of the exponential function at a given point x. Slope can also be viewed as rate of change.
For the derivative of the exponential function, here is the general method. Note that b is a number base and the function g(x) is another function of x in the exponent.
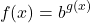
Step One: For the derivative. Take the natural logarithm of the base. This would be ln(b).
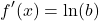
Step Two: Multiply this natural logarithm with the original exponential function f(x).

Step Three: Multiply by the derivative of the exponent g(x). You are multiplying by g'(x) via the Chain Rule.
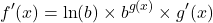
This may look complicated but let's look at some examples.

Example One
What is the derivative of two to the power of x?
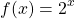
Take the natural logarithm of the base two to start.
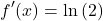
Multiply the natural logarithm by the original exponential. That is multiply by 2 to the power of x.
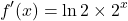
From the Chain rule take the derivative of the exponent. The derivative of x is just 1. Multiply one with the above.
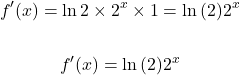
Example Two
What is the derivative of five to the power of -x?
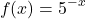
First, take the natural logarithm of five.
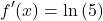
Next, copy the original exponential function and multiply this with ln(5).
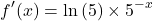
From the chain rule multiply by the derivative of the exponent. The derivative of the exponent negative x is negative one.

Example Three
Compute the derivative of ten to the power of x-cubed.
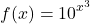
Take the natural logarithm of ten and multiply by the original exponential function.
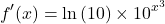
Then multiply by the derivative of the exponent. The exponent here is x cubed so the derivative of this 3 x-squared. Multiply this 3 x-squared with the other components.


Posted using STEMGeeks