
In Book 1 of Euclid’s Elements, Definition 21 reads (Fitzpatrick 6):
| Greek | English |
|---|---|
| καʹ ̓́Ετι δὲ τῶν τριπλεύρων σχημάτων ὀρθογώνιον μὲν τρίγωνόν ἐστι τὸ ἔχον ὀρθὴν γωνίαν, ἀμβλυγώνιον δὲ τὸ ἔχον ἀμβλεῖαν γωνίαν, ὀξυγώνιον δὲ τὸ τὰς τρεῖς ὀξείας ἔχον γωνίας. | 21. And further of the trilateral figures: a right-angled triangle is that having a right-angle, an obtuse-angled (triangle) that having an obtuse angle, and an acute-angled (triangle) that having three acute angles. |
In Definition 20, triangles were divided into three groups according to the lengths of their sides:
- Equilateral Triangle: All three sides are of equal length.
- Isosceles Triangle: Two and only two sides are of equal length.
- Scalene Triangle: All three sides are of different lengths.
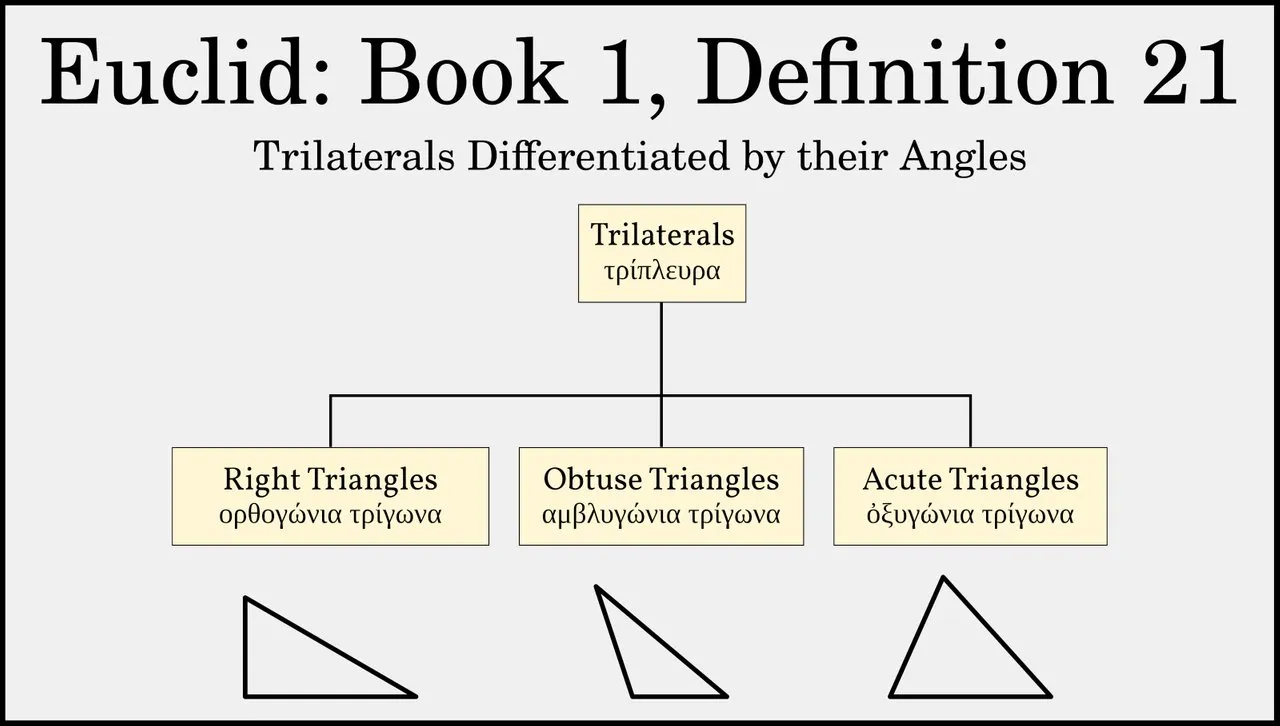
Definition 21 does something similar, but this time it is the triangle’s three angles that are taken into account:
- A right triangle—or right-angled triangle—has one right angle.
- An obtuse triangle—or obtuse-angled triangle—has one obtuse angle.
- An acute triangle—or acute-angled triangle—has three acute angles.
Definitions 10-12 defined a right angle as half a straight angle, an obtuse angle as an angle greater than a right-angle, and an acute angle as an angle less than a right angle.
Proposition 1:17 will prove that for any triangle the sum of any two angles is less than two right angles. Therefore:
- No triangle can contain more than one right angle.
- No triangle can contain more than one obtuse angle.
- No triangle can contain a right angle and an obtuse angle.
From these facts it follows that every triangle must belong to one and only one of the three categories of triangle defined in this definition.
Proclus’s Seven Triangles
In his Commentary on the First Book of Euclid’s Elements, the 5th-century philosopher Proclus notes that Definitions 20 and 21, when taken together, define seven different kinds of triangles:
| Proclus’s Seven Triangles | Definition 20 | Definition 21 |
|---|---|---|
| Equilateral | Equilateral | Acute |
| Right Isosceles | Isosceles | Right |
| Obtuse Isosceles | Isosceles | Obtuse |
| Acute Isosceles | Isosceles | Acute |
| Right Scalene | Scalene | Right |
| Obtuse Scalene | Scalene | Obtuse |
| Acute Scalene | Scalene | Acute |
There are no equilateral triangles that are right-angled or obtuse-angled. All equilateral triangles are also equiangular (and vice versa). Curiously, Euclid never proves this theorem (or the converse) explicitly, though it can be deduced from Propositions 1:5 and 1:6:
In his 20th definition in the book, Def.I.20, Euclid defines an equilateral triangle as a triangle with three equal sides. Note that he doesn’t include in his definition that the three angles must be equal, too; that would be called an equiangular triangle. Now, we all know that equilateral triangles are equiangular, but at this stage that has not been proved. If you skip forward to I.5, you’ll see a proposition that implies that equilateral triangles are equiangular, and the next proposition, I.6, implies that equiangular triangles are equilateral. (David Joyce)
Proclus’s Four-Sided Trilaterals
In his discussion of Euclid’s trilaterals, Proclus also makes the extraordinary claim that not all triangles are trilaterals:

Today, no geomater would refer to these figures as triangles. They are quadrangles, with four angles. Proclus, it seems, did not recognize the re-entrant angle—also known as a reflex angle—as an angle in the Euclidean sense. Euclid never defines reflex angles in the Elements. When he defines an obtuse angle as an angle greater than a right angle, is he assuming that all angles are less than or equal to a straight angle? Perhaps he did. When discussing Definition 9, David Joyce comments:
When the sum of angles happens to be greater than two right angles, it is continued to be treated as a sum of angles rather than an individual angle. (David Joyce)
Proclus’s idea of four-sided triangles, however, is not shared by Euclid. In the Elements, Euclid uses the terms trilateral [τρίπλευρον] and triangle [τρίγωνόν] interchangeably. In fact, he only uses the former term in Definitions 20 and 21. Thereafter, he always refers to trilaterals as triangles.
There is, in fact, no evidence that any other ancient mathematicians were of the same opinion as Proclus. Although, as Proclus concedes, some geomaters—eg Zenodorus—had special terminology to describe such re-entrant figures, they did not think of them as triangles.
Modern Editions
In his 1814 edition of the Elements, François Peyrard divided this definition into three separate definitions, numbered 27, 28 and 29 (Peyrard 4)—just as he had done with Definition 20. Ernst Ferdinand August followed suit in his edition of 1826 (August 2). In 1883, Johan Ludvig Heiberg re-integrated these into a single definition, numbered 21 (Heiberg 6-7). This is believed to correspond to Euclid’s original manuscript.
One curious discrepancy between August’s edition and the other two involves the use of the word μίαν, one in the definitions of the right and obtuse triangles. August’s use of this numeral—feminine accusative singular of εἷς—makes it explicit that a right triangle has one and only one right angle and that an obtuse triangle has one and only one obtuse angle. As we have seen, Proposition 1:17 will prove these facts, so there is no need to include them in the definitions.
And that’s a good place to stop.
References
- Ernst Ferdinand August, Euclidis Elementa, Part 1, Theodor Trautwein, Berlin (1826)
- Richard Fitzpatrick (translator), Euclid’s Elements of Geometry, University of Texas at Austin, Austin, TX (2008)
- Thomas Little Heath (translator & editor), The Thirteen Books of Euclid’s Elements, Second Edition, Dover Publications, New York (1956)
- Johan Ludvig Heiberg, Heinrich Menge, Euclidis Elementa edidit et Latine interpretatus est I. L. Heiberg, Volumes 1-5, B G Teubner Verlag, Leipzig (1883-1888)
- Glenn Raymond Morrow (translator), Proclus: A Commentary on the First Book of Euclid’s Elements, Princeton University Press, Princeton, NJ (1970)
- François Peyrard, Les Œuvres d’Euclide, en Grec, en Latin et en Français, Volumes 1-3, Charles-Frobert Patris, Paris (1814, 1816, 1818)
Online Resources
