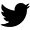Der Spieltisch beim Roulette beinhaltet die Zahlen von 1 bis 36. Die Zahlen sind in Dreierblöcken angeordnet. Addiert man die Zahlen, die in einer Zeile stehen und berechnet solange die Quersummer bis die Zahl einstellig ist, erhält man immer die Zahl 6. Das wiederholte Ausführen der Quersumme werde ich nachfolgend iterierte Quersummer (iQS) nennen. Ich bin diese Woche auf diese Kuriosität gestoßen und habe mich gefragt, warum das so ist. Hier mal ein paar Beispiele für das bessere Verständnis:
The roulette table contains the numbers from 1 to 36. The numbers are arranged in blocks of three. If you add up the numbers that are in a row and calculate the digit sum until the number is in single digits, you always get the number 6. I will call the repeated execution of the digit sum iterated digit sum (iDS) in the following. I came across this curiosity this week and wondered why. Here are a few examples for a better understanding:
| line | sum | iDS |
|---|---|---|
| 1,2,3 | 6 | 6 |
| 4,5,6 | 15 | 6 |
| 7,8,9 | 24 | 6 |
| 34,35,36 | 105 | 6 |
Ok, jetzt wo wir uns das Prinzip klar gemacht haben, suchen wir nach einem Muster, damit wir beantworten können, warum das so ist und können uns natürlich auch noch fragen, ob das auch immer so ist. Oder hört diese Kuriosität irgendwann auf?
Wenn man sich immer die erste Zahl anschaut, ist diese Zahl immer durch 3 teilbar, sobald man 1 abzieht. Die ersten Zahlen haben also die Form 3·n+1. Sprich es wird 3n+1+3n+2+3n+3 gerechnet, was 9n+6 ergibt, wobei n eine natürlich Zahl ist. Jetzt müssen wir nur noch iQS(9n+6) berechnen. Da wir uns im Dezimalsystem befinden. erhalten wir die iQS, wenn wir mod 9 rechnen.
Ok, now that we have made the principle clear, we are looking for a pattern so that we can answer why this is the case and of course we can also ask ourselves whether this is always the case. Or does this curiosity end at some point?
If you always look at the first number, this number is always divisible by 3 as soon as you subtract 1. So the first numbers have the form 3·n+1. Say we calculate 3n+1+3n+2+3n+3, which gives 9n+6, where n is a natural number. Now we just have to calculate iDS(9n+6). Since we are in the decimal system, we get the iDS if we calculate mod 9.
Das heißt also, dass die iterierte Quersumme jedes Triples auf dem Roulettetisch immer 6 ist. Und auch wenn unser Roulettetisch unendlich groß wäre, würden wir immer die Zahl 6 erhalten. Daher können wir diese Überlegung mit q.e.d. abschließen.
Man könnte sich natürlich auch noch fragen, ob dahinter eine tiefere Bedeutung steckt. Meiner Meinung nach könnte es gut möglich sein, dass "der Erfinder" des Roulettetisches einfach die Zahlen so angeordnet, weil es sterisch praktisch ist. Dennoch sei an dieser Stelle angemerkt, dass es nicht unüblich ist, dass Menschen mathemische Easter-Eggs irgendwo einbauen, aus welchen Gründen auch immer.
So this means that the iterated sum of the digits of each triple on the roulette table is always 6. And even if our roulette table were infinitely large, we would always get the number 6. Therefore, we can conclude this consideration with q.e.d..
Of course, one could also ask whether there is a deeper meaning behind this. In my opinion, it could well be that "the inventor" of the roulette table simply arranged the numbers this way because it is sterically practical. Nevertheless, it should be noted at this point that it is not unusual for people to insert mathematical aaster aggs somewhere, for whatever reason.