Bitcoin and most other cryptocurrencies today are based in part on Elliptic Curve Cryptography (ECC). What is it about ECC makes it safe to trust your hard-earned money on the Bitcoin blockchain?
Elliptic Curves
A Cartesian Coordinate System has a number of axes that are perpendicular to each other. Normally, we see this represented as a 2-dimensional plane with an X axis and a Y axis. Points can be represented on such a plane by an (x, y) pair. You count over 'x' number of units horizontally, and then count up 'y' number of units vertically, and that's your point.
A function can be used to define a collection of points. For example, y=x2 determines the value of 'y' for any given 'x' by squaring the 'x' value. This gives a parabola with a vertex located at (0, 0)
An Elliptic Curve is a special function. For Bitcoin and others, a well-known curve named "secp256k1" is used. This curve uses the formula y2=x3 + 7, and appears like this when plotted:

Given an Elliptic Curve, there are well-defined rules about how to add any two points on the curve in order to derive a third point that is also on the curve. There is also a rule about how to double any point (essentially adding it to itself) in order to derive a point. With these two rules combined, it is then possible to multiply any point by a number (known as a scalar) in order to derive another point on the curve.
Fields and Affine Points
The graph of the secp256k1 Elliptic Curve above is plotted over the group of real numbers. This means that every possible fraction on the X axis has a Y value, giving you a continuous line with no breaks. Cryptography does not use fractional numbers, though, so we need to consider only whole numbers, or integers, for any ECC work.
If we just removed the fractional parts, there would be a problem: not every integer value of X will produce an integer value of Y. For example, when x=2, y would be +/- sqrt(15), which is a fraction. So, our collection of possible points that lie on the curve are greatly reduced.
How can you do things like divide numbers, then, without resulting in fractions?
Cryptography solves this by limiting the range of possible numbers that X and Y can be. We call this limit a Finite Field of numbers defined by a prime number of elements. For example F17 is a field containing 17 elements. Because 17 is a prime number, you can take any number and divide by 17 and you will get one of 17 numbers from 0 to 16 as the remainder:
6 / 17 = 0 R 6
21 / 17 = 1 R 4
159 / 17 = 9 R 6
Notice that 6 and 159 both resulted in a remainder of 6. We say that these numbers are congruent to each other modulo 17. This is important because you can substitute 6 for any operation that has 159 in it, and get the same result (mod 17):
159 * 32 = 5088 = 299 * 17 + 5 = 5 (mod 17)
6 * 32 = 192 = 11 * 17 + 5 = 5 (mod 17)
So as far as cryptography is concerned, 6 and 159 are the same number (mod 17) because our field only has 17 numbers total (and then the pattern repeats).
This can be applied to the Elliptic Curve points, too:
Given: x = 8, we find y by:
y2 = 83 + 7
y = +/- sqrt(512 + 7) = +/- sqrt(519) = +/- sqrt(9 (mod 17))
y = +/- 3 (mod 17)
Check the result:
32 = 9 (mod 17)
9 = 9 (mod 17)
9 (mod 17) = 9 (mod 17)
So the point (8, 3) is on the curve over the field F17, as well as point (8, 14) because 17 - 3 = 14. However, not every value of x will result in a valid y. x2 must be a quadratic residue (mod 17) for it to be a valid point on the curve over F17. The collection of valid points over F17, then, are known as the affine points over that field. These are what ECC uses.
Plotting the affine points bears no resemblance to the plot of the curve over the real numbers. For example, here is what the secp256k1 curve looks like over F17:
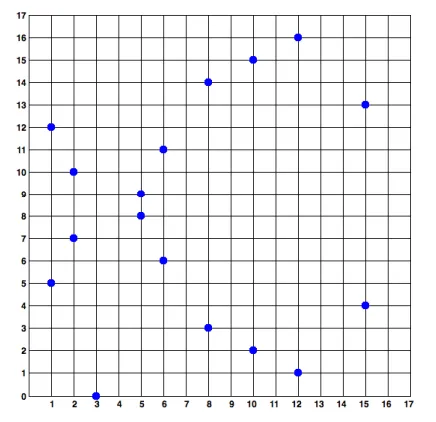
It becomes more chaotic as the size of the field grows. F59:

The actual secp256k1 curve used by Bitcoin is defined over a 256-bit prime number - any patterns that you think you may see in the above small prime plots will be completely lost if you could view the actual affine coordinates used by ECC for Bitcoin.
But, what's important to know for ECC, is that the same rules for addition and multiplication of points works - add any two affine points, and you will get a third affine point as a result. Likewise, multiply any affine point by a scalar value, and you will get an affine point as the result. Yay Math! :-)
Discrete Log Problem
If you skipped over the above introduction, here's the TLDR:
- We know how to multiply a point on an elliptic curve by a scalar number in order to get another point
- The affine points of an elliptic curve over a prime field is essentially random in nature
In Bitcoin, you have a private key that is a 256-bit number, and a public key that is an elliptic curve point. In order to generate the public key, you multiply a well-known point on the curve (known as the Generator) by your private key (a scalar) and return the coordinates of the resulting affine point.
What keeps somebody from deriving your private key (the scalar) given the public key (the Generator multiplied by the scalar)?
First, an analogy:
Working with affine points over a prime field is like having a huge stack of papers that are all out of order. Maybe the first piece of paper is labeled Page 999, the second paper is labeled Page 4, and the third paper is labeled page 12345678. You can easily count through the stack of papers to see what page number is listed on each sheet, but if I were to ask you "which piece of paper is labeled Page 17?" you wouldn't be able to do it easily.
You could start through the list and keep track of what pages you find: 999, 4, 12345678, 42, etc., until you find the one labeled 17. If the stack of papers is small enough, then this may not take much time at all. But what if that stack of papers stretched all the way to the Moon? Or to the Sun? Or to the Andromeda Galaxy?
A stack of papers that stretched to the Andromeda Galaxy, by the way, would only have an 85-bit number of pages in it. If you doubled that distance, then that would be an 86-bit number. For Bitcoin, we use a 256-bit number of pages. Let that sink in.
It is an "intractable problem" to figure out which piece of paper in the stack has a certain page number written on it. In terms of ECC, it is an intractable problem to figure out the scalar (piece of paper) that generated a point (page number) within the stack (resulting affine points from multiplying the Generator point by the scalar value).
This is known as the Elliptic Curve Discrete Log Problem, and is the foundation of everything that keeps your Bitcoin secure. If the ECDLP was ever broken, then anyone with your public key could steal your Bitcoin because they could derive your private key.
Credit for affine point plots: https://bitcoin.stackexchange.com/questions/21907/what-does-the-curve-used-in-bitcoin-secp256k1-look-like