
[Custom Thumbnail]
All the Code of the series can be found at the Github repository:
https://github.com/drifter1/compiler
Introduction
Hello it's a me again @drifter1! Today we continue with my Compiler Series, a series where we implement a complete compiler for a simple C-like language by using the C-tools Flex and Bison. In this article we will write the needed action rules for Expressions, excluding function call for now!More specifically, the topics that we will cover today are:
- Separating the operator tokens of the lexer
- Action Rules for Expressions
- Running the compiler
Requirements:
Actually you need to read and understand all the topics that I covered in the series as a whole, as these articles will give you access to knowledge about:- What Compiler Design is (mainly the steps)
- For which exact Language the Compiler is build for (Tokens and Grammar)
- How to use Flex and Bison
- How to implement a lexer and parser for the language using those tools
- What the Symbol Table is and how we implement it
- How we combine Flex and Bison together
- How we can pass information from the Lexer to the Parser
- How we define operator priorities, precedencies and associativity
- What Semantic Analysis is (Attributes, SDT etc.)
- How we do the so called "Scope Resolution"
- How we declare types and check the type inter-compatibility for different cases, including function parameters
- How we check function calls later on using a "Revisit queue", as function declarations mostly happen after functions get used (in our Language)
- Intermediate Code Representations, including AST's
- How we implement an AST (structure and management)
- Action Rules for Declarations and Initializations
Difficulty:
Talking about the series in general this series can be rated:- Intermediate to Advanced
- Medium
Actual Tutorial Content
Separating the operator tokens of the lexer
Having different operators that return the same token to the parser, we of course can't know which exact operator we have in each case. So, before getting into the actual expression rules, we first have to find a way to overcome this problem! To fix it we can set a specific value for the Value union val.ival, which depends on each operator. Value val is the token type that we chose to have for most of the tokens.More specifically, the tokens that represent more than one operators are:
- ADDOP, which is used for '+' and '-'
- INCR, which is used for "++" and "--"
- EQUOP, which is used for all the equality operators
- RELOP, which is used for all the relational operators
In the AST structure we defined some enums for all these operator types to be able to separate them in each expression node. And so it's wise to use these already defined values for the separation of the operators in the lexer. This means that we have to set the val.ival value and then return the token type to the parser.
So, the lexer.l file now contains:
...
"+" { yylval.val.ival = ADD; return ADDOP; }
"-" { yylval.val.ival = SUB; return ADDOP; }
"*" { return MULOP; }
"/" { return DIVOP; }
"++" { yylval.val.ival = INC; return INCR; }
"--" { yylval.val.ival = DEC; return INCR; }
"||" { return OROP; }
"&&" { return ANDOP; }
"!" { return NOTOP; }
"==" { yylval.val.ival = EQUAL; return EQUOP; }
"!=" { yylval.val.ival = NOT_EQUAL; return EQUOP; }
">" { yylval.val.ival = GREATER; return RELOP; }
"<" { yylval.val.ival = LESS; return RELOP; }
">=" { yylval.val.ival = GREATER_EQUAL; return RELOP; }
"<=" { yylval.val.ival = LESS_EQUAL; return RELOP; }
...Pretty simple right? Let's now get into the expressions!
Action Rules for Expressions
The grammar of our language allows many types of expressions. In general, we can say that we have the following expression cases: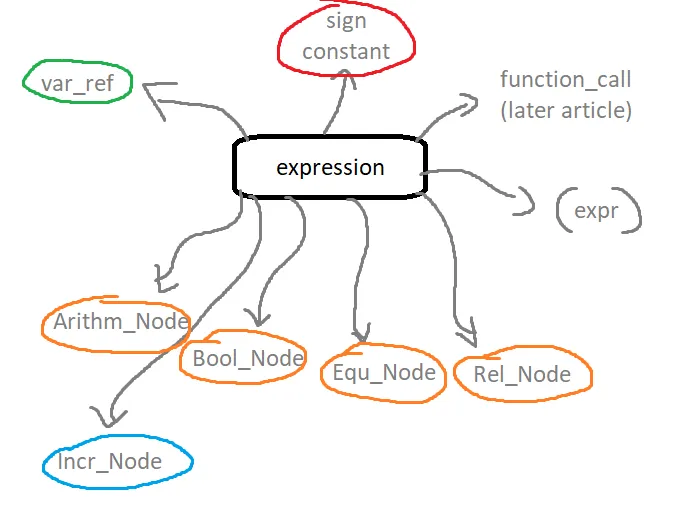
So, an expression can be:
- var_ref, which is a variable with or without reference
- sign constant, which is a constant with or without sign
- function_call, that we will cover in a later on article
- An expression in parenthesis "( )"
- Increment expression
- Arithmetic expression node
- Boolean expression node
- Equality expression node
- Relational expression node
Let's take a look at each of them, grouping similar ones together!
Variable with or without reference
A var_ref node can be visualized as following:
Let's expain this a little bit better. The "var_ref" rule has two sub-rules: "variable" and "REFER variable", where REFER is the symbol '&', mainly used for address references. As we saw last time the variable rule is used for simple variables (ID), pointers and arrays, and so for any kind of variable that can occur in our language. The variable rule gives back the variable information in form of a symbol table entry. So, this information is accessible in both sub-rules. The rule with the '&' symbol will have to "add" some new information, which tells us that we are talking about a reference of a variable. There is no entry for that in the symbol table definition, but we should also not add this information there! Any change in the symbol table entry happens globally, which is not something that we want to happen! You might have noticed that we don't have a AST Node type that stores symbol table entries yet. An expression is an AST node and so passing the information of this variable reference higher, can't be done right now!
So, where does all this all lead us into? Well, we need a new AST node type for variable references. Let's call this new Node_Type "REF_NODE" and the corresponding structure "AST_Node_Ref". This structure will store a symbol table entry and an integer value "ref", where '0' means that we have no reference, whilst '1' means that we have a reference. Creating this new structure we of course also have to create a function that creates such a node. We should don't forget to make changes in the node printing function "ast_print_node", so that it includes this new type in it's implementation.
The ast.h file will now contain:
typedef enum Node_Type {
BASIC_NODE, // no special usage (for roots only)
// declarations
DECL_NODE, // declaration
CONST_NODE, // constant
// statements
IF_NODE, // if statement
ELSIF_NODE, // else if branch
FOR_NODE, // for statement
WHILE_NODE, // while statement
ASSIGN_NODE, // assigment
SIMPLE_NODE, // continue, break and "main" return statements
INCR_NODE, // increment statement (non-expression one)
FUNC_CALL, // function call
// expressions
ARITHM_NODE, // arithmetic expression
BOOL_NODE, // boolean expression
REL_NODE, // relational expression
EQU_NODE, // equality expression
REF_NODE, // identifier in expression
// functions
FUNC_DECL, // function declaration
RETURN_NODE, // return statement of functions
}Node_Type;
...
typedef struct AST_Node_Ref{
enum Node_Type type; // node type
// symbol table entry
list_t *entry;
// reference or not1
int ref; // 0: not reference, 1: reference
}AST_Node_Ref;
...
AST_Node *new_ast_ref_node(list_t *entry, int ref);
...In the ast.c the node creation is implemented such as:
AST_Node *new_ast_ref_node(list_t *entry, int ref){
// allocate memory
AST_Node_Ref *v = malloc (sizeof (AST_Node_Ref));
// set entries
v->type = REF_NODE;
v->entry = entry;
v->ref = ref;
// return type-casted result
return (struct AST_Node *) v;
}The print node function has no big changes and so I will leave it to you to go to GitHub to check it out :P
So, by having this new node type we can now set the types of the non-terminals that occur in expressions in general and the case that we are covering right now. The "var_ref" rule of course has to be of type "node" being a AST_Node. Of course an expression is also a node and so we have the following non-terminal definition:
%type <node> expression var_ref
In the expression rule we only have to set the expression node equal to the node that was created by the var_ref rule. So, the actual work will be done in the actual var_ref rule. Depending on the case, var_ref will create an AST_Node of the type "Ref_Node" with or without reference, which is denoted by the value of the second parameter "ref".
These action rules look as following:
expression:
... other sub-rules ...
| var_ref
{
$$ = $1; /* just pass information */
}
... other sub-rules ...
;
...
var_ref: variable
{
$$ = new_ast_ref_node($1, 0); /* no reference */
}
| REFER variable
{
$$ = new_ast_ref_node($2, 1); /* reference */
}
;
...Constant with or without sign
This is a somewhat simple case that can be visualized as following: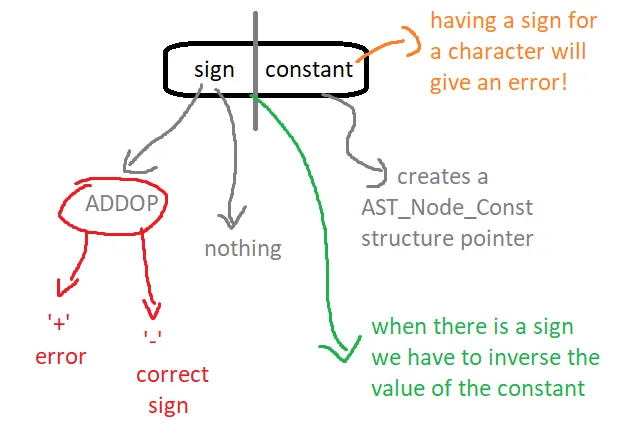
The "sign constant" rule is build up of a constant, that already stores a constant in form of an constant AST node and the optional sign rule. The sign rule either is an ADDOP (where we will have to check if it's an '-') or nothing/empty. Storing an integer value in form of the Value.ival entry we can pass this information over to the "sign constant" rule, through the sign rule. Let's say that '0' means no sign, whilst '1' means a sign which of course is also correct. When having a sign we of course have to inverse the value of the constant depending on the constant type, which is pretty easy to do using a switch case statement!
The token definition of the sign rule is:
%type <val> signAnd so the action code for these rules is:
expression:
... other sub-rules ...
| sign constant
{
/* sign */
if($1.ival == 1){
AST_Node_Const *temp = (AST_Node_Const*) $2;
/* inverse value depending on the constant type */
switch(temp->const_type){
case INT_TYPE:
temp->val.ival *= -1;
break;
case REAL_TYPE:
temp->val.fval *= -1;
break;
case CHAR_TYPE:
/* sign before char error */
fprintf(stderr,
"Error having sign before character constant!\n");
exit(1);
break;
}
$$ = (AST_Node*) temp;
}
/* no sign */
else{
$$ = $2;
}
ast_traversal($$); /* just for testing */
}
... other sub-rules ...
;
sign: ADDOP
{
/* plus sign error */
if($1.ival == ADD){
fprintf(stderr, "Error having plus as a sign!\n");
exit(1);
}
else{
$$.ival = 1; /* sign */
}
}
| /* empty */
{
$$.ival = 0; /* no sign */
}
;
...Simple cases
The parenthesis and increment rules are pretty easy to do. The parenthesis is the easiest of them all, as the "parent" expression just has to get the value of the expression inside of the parenthesis. In the same way, storing the increment or decrement type inside of the token INCR and knowing the position (prefix or postfix) of the operator in the expression, we can easily create a Incr-Node! So, let's do this!expression:
... other sub-rules ...
| ID INCR
{
/* increment */
if($2.ival == INC){
$$ = new_ast_incr_node($1, 0, 0);
}
else{
$$ = new_ast_incr_node($1, 1, 0);
}
ast_traversal($$); /* just for testing */
}
| INCR ID
{
/* increment */
if($1.ival == INC){
$$ = new_ast_incr_node($2, 0, 1);
}
else{
$$ = new_ast_incr_node($2, 1, 1);
}
ast_traversal($$); /* just for testing */
}
... other sub-rules ...
| LPAREN expression RPAREN
{
$$ = $2; /* just pass information */
}
... other sub-rules ...
;
Operator cases
The rest of the operators can be summarized in the following visualization: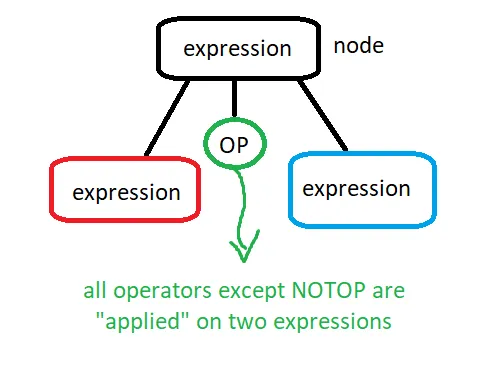
All the operators are very simple. They have a left and right side and a operator depending on their type which can be: arithmetic, boolean, equality and relational. The information about the exact type of operator is either directly known from the token (token of one operator) or is stored in the token inside of the Value.ival entry. All except the NOTOP operator have two childs (left an right). For the NOTOP operator we add the single operand as the left child, whilst the other is NULL.
In code the action rules are:
expression:
expression ADDOP expression
{
$$ = new_ast_arithm_node($2.ival, $1, $3);
ast_traversal($$); /* just for testing */
}
| expression MULOP expression
{
$$ = new_ast_arithm_node(MUL, $1, $3);
ast_traversal($$); /* just for testing */
}
| expression DIVOP expression
{
$$ = new_ast_arithm_node(DIV, $1, $3);
ast_traversal($$); /* just for testing */
}
... other sub-rules ...
| expression OROP expression
{
$$ = new_ast_bool_node(OR, $1, $3);
ast_traversal($$); /* just for testing */
}
| expression ANDOP expression
{
$$ = new_ast_bool_node(AND, $1, $3);
ast_traversal($$); /* just for testing */
}
| NOTOP expression
{
$$ = new_ast_bool_node(NOT, $2, NULL);
ast_traversal($$); /* just for testing */
}
| expression EQUOP expression
{
$$ = new_ast_equ_node($2.ival, $1, $3);
ast_traversal($$); /* just for testing */
}
| expression RELOP expression
{
$$ = new_ast_rel_node($2.ival, $1, $3);
ast_traversal($$); /* just for testing */
}
... other sub-rules ...
;Running the compiler
Running the compiler for the "full_example.c" file, the compiler prints out the following info-messages: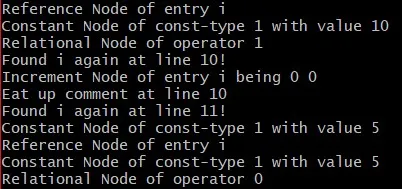

So, our compiler now detects the types of expressions that occur during the syntax analysis. We use the traversal function on each node, which explains why some nodes get print out more than one times! Constants, reference nodes etc. are childs of other nodes and so get print out on their own, but also during the traversal of their parent nodes...and the parent nodes of their parent nodes.
Note that we will also have to do type checking someday in the future!
RESOURCES
References:
No references, just using code that I implemented in my previous articles.Images:
All of the images are custom-made!Previous parts of the series
- Introduction -> What is a compiler, what you have to know and what you will learn
- A simple C Language -> Simplified C, comparison with C, tokens, basic structure
- Lexical Analysis using Flex -> Theory, Regular Expressions, Flex, Lexer
- Symbol Table (basic structure) ->Why Symbol Tables, Basic Implementation
- Using Symbol Table in the Lexer -> Flex and Symbol Table combination
- Syntax Analysis Theory -> Syntax Analysis, grammar types and parsing
- Bison basics -> Bison tutorial actually
- Creating a grammar for our Language -> Grammar and first Parser
- Combine Flex and Bison -> lexer and parser combined
- Passing information from Lexer to Parser -> Bug Fix, yylval variable, YYSTYPE union, Setting up the Parser, Passing information "directly" and through the symbol table (special case) with examples.
- Finishing Off The Grammar/Parser (part 1) -> Adding the missing grammar rules, small fixes
- Finishing Off The Grammar/Parser (part 2) -> Operator priorities, precedencies and associativity, complete example file (for testing), grammar rule visualization, finish off grammar/parser
- Semantic Analysis Theory -> What is Semantic Analysis about, CSG and CSL, Attribute Grammars, Syntax Directed Translations (SDT)
- Semantics Examples -> Visualization of Semantics for different rules/cases, needed attributes, what we have to implement from now on
- Scope Resolution using the Symbol Table -> What we have now, scope resolution, integration, compiler output
- Type Declaration and Checking -> Type declaration and type checking code, "simple" code integration
- Function Semantics (part 1) -> Code for parameter definitions, function declarations and parameter compatibility checking
- Function Semantics (part 2) -> Revisit queue concept, basic implementation, inserting undeclared identifiers
- Abstract Syntax Tree Principle -> Intermediate code generation and representations, how to design an AST
- Abstract Syntax Tree Structure -> Node, operator and value types, AST node structures, some management functions, integration with the rest of the compiler
- Abstract Syntax Tree Management -> Tweaking Nodes, Node creation and AST traversal functions, "manual" testing of the AST
- Action Rules for Declarations and Initializations -> Replacing many values with a Value union, Other smaller changes, Action rules for declarations, Action rules for initializations
Final words | Next up on the project
And this is actually it for today's post! I hope that I explained everything as much as I needed to, meaning that you learned something out of it.Next up on this series are:
- Semantic analysis (using more action rules in Bison)
- Intermediate Code generation (using the AST structure for more cases)
- Machine Code generation (MIPS Assembly)
So, see ya next time!
GitHub Account:
https://github.com/drifter1
Keep on drifting! ;)
