
[Custom Thumbnail]
All the Code of the series can be found at the Github repository:
https://github.com/drifter1/circuitsim
Introduction
Hello it's a me again @drifter1! Today we continue with the Electric Circuit Simulation series, a tutorial series where we will be implementing a full-on electronic circuit simulator (like SPICE) studying the whole concept and mainly physics behind it! In this article we will cover the Nodal Analysis Method, which is based on Kirchhoff's Current Law (KCL) and is used to calculate Node Voltages.Requirements:
- Physics and more specifically Electromagnetism Knowledge
- Knowing how to solve Linear Systems using Linear Algebra
- Some understanding of the Programming Language Python
Difficulty:
Talking about the series in general this series can be rated:- Intermediate to Advanced
- Intermediate
Actual Tutorial Content
Nodal Analysis Method
Nodal (Node-Voltage) Analysis is based on Kirchhoff's Current Law (KCL), which means that it's used to calculate the voltage in the various Nodes of the Circuit. This method is used in the popular circuit simulator: SPICE, and the same modification of this technique will also be used in our simulator! So, what exactly does this method do? Well, using a very efficient way of organizing the information from a circuit, we find the so called node voltage of all except one nodes of the circuit. The remaining node is called the reference node and almost always called the ground node. The potential of this ground node is defined to be 0V (In spice net-lists node 0 is the reference node). The potential of all the other nodes is measured relative to the ground.Node Voltage
Before continuing with the steps of the method, we should first define what node voltage means! The voltage across the terminals of a single element is called an element voltage or branch voltage (as all elements are considered to be branches of the circuit). With node voltage we are referring to the potential difference between two nodes of the circuit, where a node is the connection point between two or more circuit elements or branches.For example let's suppose that we have the following circuit:
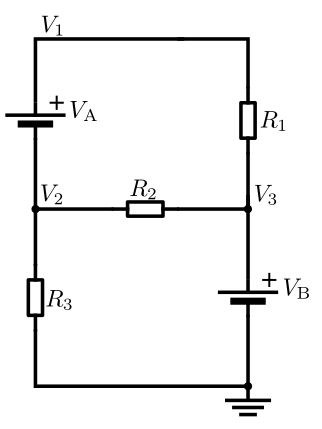
[Image 1]
In this circuit there are 4 nodes and so we have to calculate 3 node voltages, because we "grounded" one of them to 0V. To apply KCL we also have to define which node has the largest potential in each potential difference (or voltage) calculation. This means that we will also have to suppose some current direction. If the current moves from some node A to another node B, and so from the + to the - pole of the element/branch, then the voltage is:
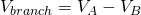
(In this case VA has more potential)
If the current moves from B to A, then the voltage is:
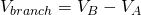
(In this case VB has more potential)
So, now that we have a way to calculate the voltage for each element, what's the voltage of the elements: R1, R2 and R3, in the case of the example circuit? Well, supposing V1 > V2 > V3 we have:

As always the direction of the current or the random hypothesis of which node has the larger potential will not have such a big impact on the result. The result might just turn out to be negative, telling us that we chose the wrong direction. The voltage of R3 is considered to be an easy node case, cause one node is the reference node. As you might expected already, the reference node can be any of the nodes of the circuit. So, we tend to select the node that "puts" the most zeros into the potential difference! Of course, this can't be automated that easily and so node 0 is selected "randomly" or directly from the net-list file...
Nodal Analysis Steps
Thinking about how KCL works (identify nodes, assign current directions, write KCL, solve linear system, solve for other currents and voltages using Ohm's Law), the steps of Nodal Analysis are:- Identify the nodes of the circuit by also choosing one to be the ground node
- Assign labels to each node, by also supposing some current direction
- Write the KCL equations for all except the ground node
- Solve the resulting linear system for all node voltages
- Solve for other element currents and voltages you want using Ohm's Law
Nodal Analysis Example
Let's consider the following electronic circuit from Khan Academy: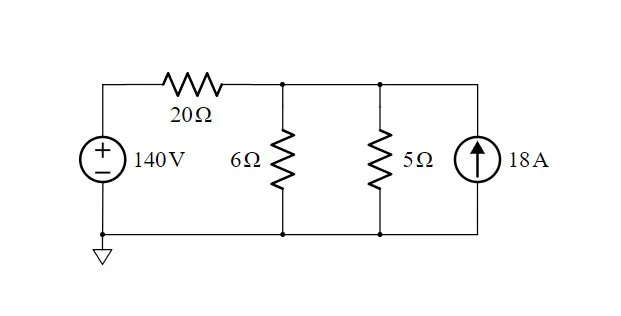
[Image 2]
Let's apply Nodal Analysis to calculate the Current and Voltage of all Elements!
1. Identify Nodes
The circuit has the following 3 nodes: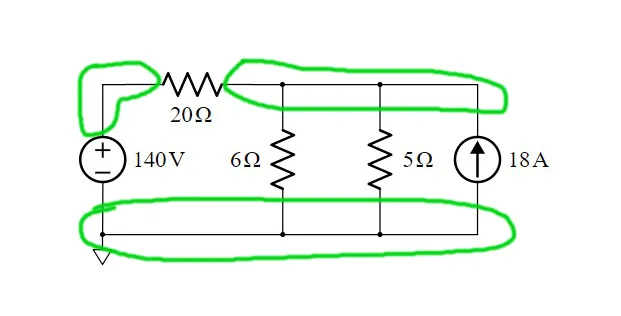
2. Assign Node Labels
Let's assign the labels 0, A and B to the nodes, where 0 is the ground node: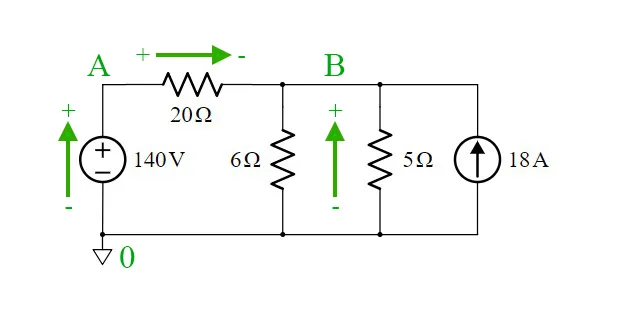
3. Write KCL Equations
Before we get into KCL, we should recall how exactly KCL works. We can apply KCL as "sum of entering = sum of leaving currents" or we can also suppose that all are entering or leaving the node, by putting a negative sign if the current does the opposite. That way we will end up with something in the form: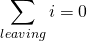
So, instead of thinking about larger, smaller etc. we can just assume that all currents are leaving the node. Thus, the potential of the node that we are solving is supposed to be larger than the potential of the other nodes in the equation. In other words, the circuit's currents are as following:
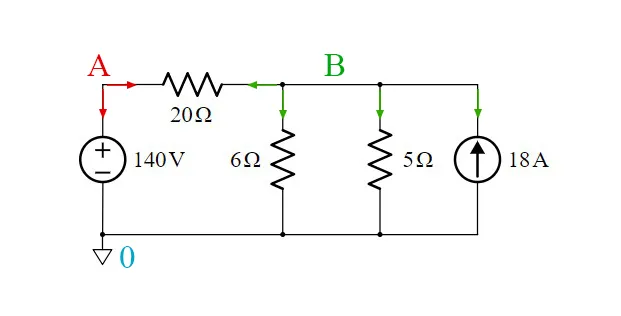
So, with all that in mind, let's start with node A. Without even thinking about the direction of currents in node A, we can already say that the voltage of Node A is equal to the voltage of the voltage source, which is 140V. Therefore:
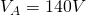
For node B we apply the "leaving" trick:

4. Solve the Linear System
Let's now solve the linear system! Of course this one is quite simple, as we already know the value of voltage for node A (VA). Either way we have:
As you can see both voltages came out positive, as we never really supposed a current direction!
5. Solve for other Currents and Voltages
Let's now also find the unknown currents across all the resistors! This can be done pretty easily by applying Ohm's Law:
Manual Python Implementation
To understand how we will get into the Circuit Simulator applying this exact method, let's solve the previous problem using Python! You will again see that the method can't be automatized right now, which means that we will have to modify it a little bit...Either way, the code for solving the previous problem is:
import numpy as np
'''
Electronic Circuit is
+┌─ R1 ┬─────┬────┐
V R2 R3 I ↑
-└─────┴─────┴────┘
with following values:
'''
V = 140
I = 18
R1 = 20
R2 = 6
R3 = 5
'''
1/2. Identify and Assign Nodes
Node 0: Connecting V-R2-R3-I (node at the bottom)
Node A: Connecting V-R1 (upper left node)
Node B: Connecting R1-R2-R3-I (upper right node)
'''
# 3. Apply KCL for Nodes A and B
# Node A
# simple case with VA = V
VA_nodeA = 1
VB_nodeA = 0
b_nodeA = V
# Node B
# (VB-VA)/20 + VB/6 + VB/5 - 18 =0
# ...
# 25 VB + (-3) VA = 1080
VA_nodeB = -(1/R1)*60
VB_nodeB = ((1/R1) + (1/R2) + (1/R3))*60
b_nodeB = I*60
# 4. Solve the Linear System
# 1 VA + 0 VB = 25
# - 3 VA + 25 VB = 1080
a = np.array([[VA_nodeA, VB_nodeA],[VA_nodeB, VB_nodeB]])
b = np.array([b_nodeA, b_nodeB])
# Solve System
x = np.linalg.solve(a,b)
print(x)
# 5. Solve for other Currents and Voltages
V20 = (x[0] - x[1])/R1
print("v20: ", V20)
V6 = (x[1])/R2
print("v6: ", V6)
V5 = (x[1])/R3
print("v5: ", V5)Running this code we get the same results as before:
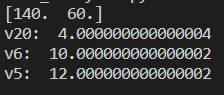
You can see that the A-matrix contains only Conductance (1 / Resistance), whilst the b-matrix contains only Currents. This might already make you think about an automation, but either way, let's wait for the next articles to make the Inspection in the correct way!!
RESOURCES
References:
- https://www.khanacademy.org/science/electrical-engineering/ee-circuit-analysis-topic/ee-dc-circuit-analysis/a/ee-node-voltage-method
- https://www.tutorialspoint.com/network_theory/network_theory_nodal_analysis.htm
- https://www.electronics-tutorials.ws/dccircuits/dcp_6.html
Images:

- https://www.khanacademy.org/science/electrical-engineering/ee-circuit-analysis-topic/ee-dc-circuit-analysis/a/ee-node-voltage-method
Mathematical Equations were made using quicklatex
Previous parts of the series
- Introduction
- Electromagnetism Background (part 1)
- Electromagnetism Background (part 2)
- Mesh Analysis
Final words | Next up on the project
And this is actually it for today's post! I hope that the Full-on example and "Manual" Python Implementation helped you understand what this method is all about!Next up on this series we will modify the two methods that we covered (Mesh and Nodal Analysis) by Inspection to create the Linear System somewhat automatically, without having to apply KVL and KCL correspondingly.
So, see ya next time!
GitHub Account:
https://github.com/drifter1
Keep on drifting! ;)
