
[Custom Thumbnail]
All the Code of the series can be found at the Github repository:
https://github.com/drifter1/circuitsim
Introduction
Hello it's a me again @drifter1! Today we continue with the Electric Circuit Simulation series, a tutorial series where we will be implementing a full-on electronic circuit simulator (like SPICE) studying the whole concept and mainly physics behind it! In this article we will modify Kirchhoff's Laws, using a concept of Graph Theory which is called an Incidence Matrix. Doing that, we will be one step closer to the automation of the linear system creation...Requirements:
- Physics and more specifically Electromagnetism Knowledge
- Knowing how to solve Linear Systems using Linear Algebra
- Some understanding of the Programming Language Python
Difficulty:
Talking about the series in general this series can be rated:- Intermediate to Advanced
- Intermediate
Actual Tutorial Content
Incidence Matrix
For a graph G of n vertices and m edges, we define a n x m incidence matrix I(G) or A0. The elements of the matrix show us how many times vertex vi is incident to edge ej. Don't confuse it with the adjacency matrix that is a graph representation.Either way, the general form of an incidence matrix is:
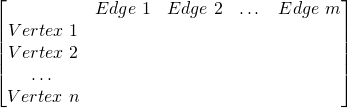
In the case of un-directed graphs, we put:
- 1, whenever edge j is connected to vertex i
- 0, if not
In the case of directed graphs, we put:
- 1, whenever edge j is "leaving" vertex i
- -1, whenever edge j is "entering" vertex i
- 0, if not
Reduced Incidence Matrix
The reduced incidence matrix A is obtained by deleting any row of the incidence matrix A0. Thinking about Nodal Analysis this will be quite useful as one of the vertices is somewhat "eliminated" (reference or ground node) and of no use in the linear system. So, we will always remove the row about the 0th node...Example
Before we get into Kirchhoff's Laws and how they are modified based on Incidence Matrices, let's first create the incidence matrix for a simple directed graph.Suppose the following Graph:
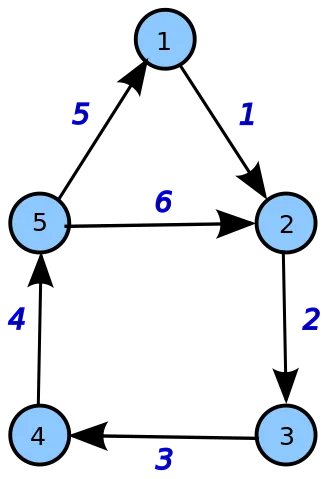
[Image 1]
As you can see this Graph contains 5 vertices and 6 edges. Based on the rules for directed graphs (1 when "leaving", -1 when "entering", 0 else), the Incidence Matrix of this Graph is:

Supposing that the Graph represents some Electronic Circuit, we would put the ground node at one of the vertices with the most entries in its row of the Incidence Matrix. So, the ground node would be Vertex 2 or 5. Selecting vertex 5 and so the 5th row, the Reduced Incidence Matrix is:

Modified Kirchhoff Laws
Notations
Before we get into the modified versions of Kirchhoff's Laws, we should first explain the various notations of symbols that we will use in the equations. Even though we use common quantities and symbols, some might look very similar (E.g. v and u) in LaTeX.The Mathematical notations are:

In the Modified Laws we will be using:
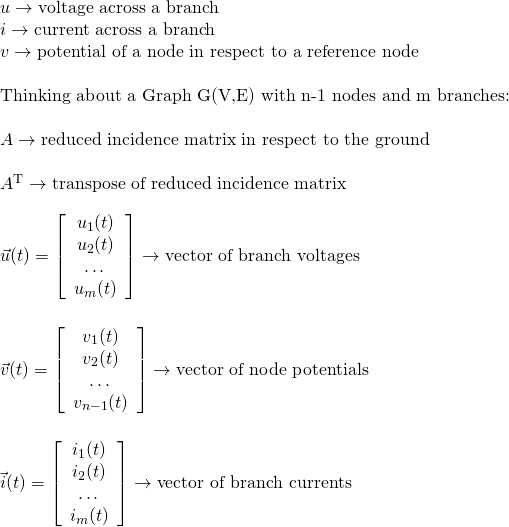
The dimensions of the matrices and vectors are:
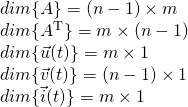
Using all this we can now rewrite the Kirchhoff Laws...
Modified KCL
KCL tells us that the the sum of all currents leaving a node is equal to the sum of all current entering the node. Putting a positive sign when they are leaving and a negative sign when they are entering the total sum of all currents is zero. Thinking about the Incidence Matrix, this matrix gives us the sign of the currents in the sum and so using only the Reduced Incidence Matrix A and the vector of branch currents i(t) we can write KCL as: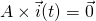
Modified KVL
Instead of using the "classic" KVL Law that tells us that the voltage sum of any loop is equal to zero, we will be using the transpose incidence matrix, node potential vector and branch voltage vector, to define the voltage of each branch as the potential difference between the nodes that the branch is connected with. The incidence matrix will tell us if the voltage is positive or negative. So, KVL becomes: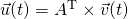
Full-On Example
Consider the following electronic circuit:
Made with Circuit Diagram
This circuit has 3 vertices and 5 edges, which can be any circuit element. Selecting one of the vertices to be the ground node (as it is shown in the diagram), we can create the following Reduced Incidence Matrix:
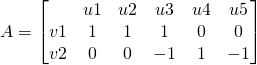
where we consider the currents i1, i2, i3 to be leaving node v1, i4 to be leaving v2 and i5 to be entering v2. That way each of them is basically entering or leaving each circuit element.
KCL for this circuit looks like this:
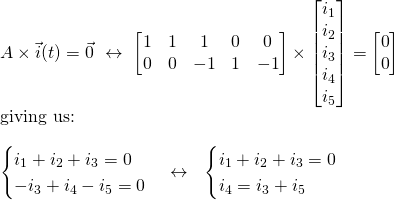
KVL for this circuit looks like this:
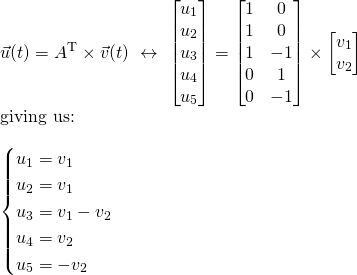
In this previous example the rectangles could be anything and so the value or equation of each edge (ui) is quite diverse. Remembering how Nodal Analysis had trouble with voltage sources and Mesh Analysis had trouble with current sources, we will use today's concept of the Incidence Matrix and the Modified versions of Kirchhoff's Laws (KCL and KVL) in the next articles to make another modification to Nodal Analysis. That way this method will be able to cover elements that can be written in respect to current and elements that cannot be written in respect to current, but only voltage. To keep things simple in the beginning we will first make a Static (or DC) Analysis of Electronic Circuits, where the behavior of Capacitors and Inductors is "static" (the first acts like an open circuit, whilst the second acts like a simple wire).
RESOURCES
References:
- http://mathonline.wikidot.com/incidence-matrices
- http://www-inst.eecs.berkeley.edu/~ee100/fa08/lectures/EE100supplementary_notes_11c.pdf
- https://basicelectronicsguide.blogspot.com/2018/07/incidence-matrix.html
Images:
Mathematical Equations were made using quicklatex
Previous parts of the series
- Introduction
- Electromagnetism Background (part 1)
- Electromagnetism Background (part 2)
- Mesh Analysis
- Nodal Analysis
- Modified Mesh Analysis by Inspection
- Modified Nodal Analysis by Inspection
Final words | Next up on the project
And this is actually it for today's post! I hope that I was able to explain everything as much as needed!Based on what we covered today, next time we will modify Nodal Analysis again to automate the generation of the Linear System for Static (or DC) Analysis...something that might take more than one article complete (not quite sure yet).
So, see ya next time!
GitHub Account:
https://github.com/drifter1
Keep on drifting! ;)

