Lo maravilloso de estudiar el alcance de los números, como un sistema que utiliza símbolos o dígitos reconocidos universalmente para contar o medir cualquier parámetro, es que su clasificación los va englobando por conjuntos de números que dan respuesta a las distintas situaciones que se presentan a la hora de realizar simples operaciones aritméticas a diferentes representaciones algebraicas.

En las operaciones aritméticas básicas se deben considerar los operadores + (suma), − (resta), × (multiplicación) y / (división), pero es que en la actualidad se consideran expresiones aritméticas la potencia (^) y la división modular o porcentual (%). Aunque ya estamos acostumbrados a trabajar con estos operadores matemáticos, lo más crítico es discriminar y estar atentos con la clasificación principal de los números.

12 + Y = 8

, ¿Qué número debo sumarle a 12 para que el resultado sea 8?

Insisto en la importancia de conocer el conjunto de números que estemos trabajando, por ejemplo en este caso, se reconoce a la clasificación de números enteros, al conjunto ℤ = {. . . ., −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, . . . .}

Los números RACIONALES (m/w)

, NO pertenecen ni a los números NATURALES ni a los números ENTEROS, se expresan como el cociente de 2 números ℤ, por lo que son una fracción del conjunto.

De esta manera se va extendiendo la amplia gama de los números hasta la clasificación general de los números COMPLEJOS, para dar solución al problema de la ecuación cuadrática cuya igualdad es −1.

Los números COMPLEJOS

En publicaciones anteriores y en alto porcentaje trabajé con números REALES, sobretodo cuando usaba expresiones con potencias de grado 2 para resolver el Teorema de Pitágoras, donde existe la restricción que la raíz cuadrada de un número positivo existe en los ℝ, así la raíz principal será un número > 0.

---

Entonces como la restricción en los números REALES para una expresión cuadrática, por ejemplo, debe ser positivo el radicando, en caso contrario no existe solución en los ℝ.

---

Se introdujo el número IMAGINARIO

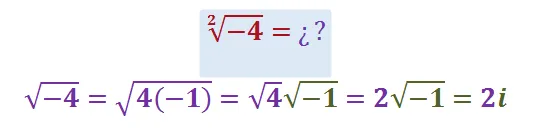
Aunque puede llevar asociada una inconsistencia al aplicar las propiedades de la potenciación que funciona muy bien con los números ℝ⁺, la introducción del número i = √ −1 concluye la interrogante de que si existe un número que elevado al cuadrado de como resultado −1, pues se "construyen" nuevos números que contienen una parte ℝ y una parte imaginaria con la unidad compleja C i. ​

Apoyo bibliográfico y fuente de imágenes

Nuestras ideas y conocimientos que podamos tener sobre el tema tratado en este artículo pueden ampliarse de manera voluntaria al consultar el siguiente catálogo de referencias:

• Imagen de Fir0002: Portada con lo realmente complejo
• Guía de aprendizaje: ¿Qué son los números naturales?
• Imagen de fondo joiom: Fondo de números
• Imagen de HB: Subconjuntos de números complejos
• Wikipedia: Number

Las funciones matemáticas son expresiones que relacionan
las variables de una igualdad,
así que invariablemente encontraremos alguna solución