Hello it's a me again Drifter Programming! Today we will continue on with Java Graphs talking about Traversal Algorithms and more particularly the BFS and DFS Algorithms! You can find the last post here and today would be also a great Idea to check the Datastructures here also out! I will start out talking about some Theory about those 2 and then get into the Implementation part! So, without further do let's get started!
Traversal Algorithms:
Before starting out with the implementation we should first start out talking about why we need those 2 algorithms. Well, the answer is simple. Last time we already did some kind of Printing of the Graph and there we only showed where we can go directly from one Vertex to another (adjacent Vertex). But, we also need a way of knowing if we can reach a specific Vertex starting from another Vertex and "taking Edges" continuously. So, this algorithms will give us a way of searching the Graph for a specific Vertex, but starting from another one!
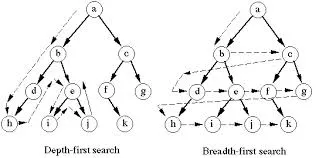
Well, now you might be thinking: "Yeah we want this functionality, but why 2 algorithms? What makes them differentiate?". We can do this searching using 2 concepts. Breadth First Search (BFS) aims to traverse the Graph as close as possible to the starting Vertex. Depth First Search (DFS) on the other hand tries to reach far Vertexes. That's why BFS uses a Queue to implement so that we can take the Vertex that was inserted first. DFS uses a Stack so that it takes the last inserted Vertex. BFS uses a Boolean Array for each Vertex to store if we have visited (seen) the specific Vertex. DFS uses a Byte Array to store a Color that can be white (0), grey (1) or black (2). White means ths Vertex is unvisited, grey means we are currently visiting it and black means we are finished with it.
The Steps for BFS are:
- Insert the starting Vertex to the Queue and mark it as seen
- Loop until the queue is empty
- Take/Remove Vertex from the Queue and Insert its adjacent Vertices that were not seen to the Queue and mark them as seen
The Steps for DFS are:
- Insert the starting Vertex to the Stack
- Loop until stack is empty
- Take/Remove Vertex from the Stack and if it is white, paint it grey, add it's adjacent Vertices to the Stack and then paint it black
Off course you can implement the algorithms in other ways also, but I found it easier in Code to do things this way! Using this Steps you can also do the steps by hand!
After all that we can actually already start implementing those Algorithms!
Graph Implementation:
We will use the Adjacency List Graph Implemenation of last time, but change it a little bit. We actually will now make our Graph Directed inserting/removing only one of the two Edges that 2 Vertices can be connected with. It will actually don't change a lot on the Testing part, but we will understand the Traversal better, cause if for example 0 is never the second Vertex of an Directed Edge and we start from another Vertex we will never be able to get to 0! I also forgot to include a way of getting the verticecount and so we will add also a Getter for the vCount Variable!
So, our Graph now looks like this:
import java.util.ArrayList;import java.util.Iterator;import java.util.List;public class Graph { private int vCount; private List<Integer>[] adj; public int getvCount() { return vCount; }
public Graph(int vCount) { this.vCount = vCount; adj = (List<Integer>[]) new List[vCount]; for (int i = 0; i < vCount; i++) adj[i] = new ArrayList<Integer>(); }
public void addEdge(int i, int j) { adj[i].add(j); }
public void removeEdge(int i, int j) { Iterator<Integer> it = adj[i].iterator(); while (it.hasNext()) { if (it.next() == j) { it.remove(); return; } } }
public boolean hasEdge(int i, int j) { return adj[i].contains(j); }
public List<Integer> neighbours(int vertex) { return adj[vertex]; }
public void printGraph() { for (int i = 0; i < vCount; i++) { List<Integer> edges = neighbours(i); System.out.print(i + ": "); for (int j = 0; j < edges.size(); j++) { System.out.print(edges.get(j) + " "); } System.out.println(); } }}BFS Implementation:
I already talked a lot about the implementation of this algorithm previously. We will use a LinkedList as a Queue and a Boolean "seen" Array with each index representing if a Vertex was visited. Then we actually just follow the algorithmic steps and also print out the vertices to which we can go starting off from another Vertex!
So, our Code looks like this:
public static void bfs(Graph g, int v) { boolean[] seen = new boolean[g.getvCount()]; LinkedList<Integer> q = new LinkedList<Integer>(); // queue-like q.add(v); seen[v] = true; while (!q.isEmpty()) { int i = q.remove(); for (Integer j : g.neighbours(i)) { if (!seen[j]) { q.add(j); seen[j] = true; } } } System.out.print(v + " -> "); for (int i = 0; i < seen.length; i++) { if (seen[i]) System.out.print(i + ", "); } System.out.println();}DFS Implementation:
We also talked about this implementation already. We will use a byte array that will contain 3 different color byte values that represent if we have visited (black), are currently visiting (grey) or don't visited (white) a specific Vertex. We will use a Stack that will store the Vertices to be visited and follow the algorithmic steps I already told you. Lastly we will again print to which Vertices we can go starting from a specific Vertex checking if the byte value is Black or not!
So, our Code looks like this:
public static void dfs(Graph g, int v) { byte white = 0, grey = 1, black = 2; byte[] c = new byte[g.getvCount()]; Stack<Integer> s = new Stack<Integer>(); s.push(v); while (!s.isEmpty()) { int i = s.pop(); if (c[i] == white) { c[i] = grey; for (int j : g.neighbours(i)) s.push(j); c[i] = black; } } System.out.print(v + " -> "); for (int i = 0; i < c.length; i++) { if (c[i] == black) System.out.print(i + ", "); } System.out.println();}Testing on same Graph and Starting Vertex:
Let's finally now use those Algorithms on the same Directed Graph and calling both for the same starting Vertex!
import java.util.LinkedList;import java.util.Stack;public class TestGraphs { public static void main(String[] args) { Graph g = new Graph(5);
System.out.println("Graph:"); // add Edges g.addEdge(0, 1); g.addEdge(0, 3); g.addEdge(1, 3); g.addEdge(1, 4); g.addEdge(2, 1); g.addEdge(2, 3); g.addEdge(3, 4); g.addEdge(4, 2);
// print Graph g.printGraph();
// Traversal Algorithms System.out.println("BFS:"); bfs(g, 0); bfs(g, 1);
System.out.println("DFS:"); dfs(g, 0); dfs(g, 1); } // BFS and DFS Functions need to be put here :)}Running this we will get the following in our Console:
Graph:
0: 1 3
1: 3 4
2: 1 3
3: 4
4: 2
BFS:
0 -> 0, 1, 2, 3, 4,
1 -> 1, 2, 3, 4,
DFS:
0 -> 0, 1, 2, 3, 4,
1 -> 1, 2, 3, 4,
You can see that we can go everywhere from 0, but 1 (2, 3 and 4 too if you test it out) cannot go to 0, cause there is no Edge that goes back to 0.
This is actually it for today! Hope you enjoyed it!
Until next time...Bye!
