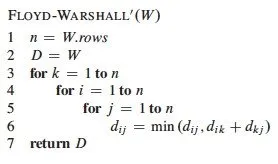
Hello its me again drifter1! Today we get into Java again talking about the 2 main All Pair Shortest Path Algorithms that are used in Graphs. I will mainly talk about the Floyd Warshall algorithm that we will also implement and I will also explain how the Johnson algorithm works. You can check out the previous post with the single-source Bellman-Ford algorithm here! So, without further do let's get started!
All pair shortest path problem:
Let's first get into what this problem is all about. We already know that with a single-source algorithm we can find the shortest path from one (source) vertex to any other vertex in the graph. But, in many circumstances we may need to find the shortest path from any vertex to any other vertex. This is when a APSP algorithm is needed and becomes useful.
Think about a network where the computers are connected together randomly like a graph. Suppose one of the computers wants to send a message to another, but this message needs to get to it's destination in the quickest time possible. Here we can use a single-source algorithm to find the shortest path to the destination. But, what if another computer wants to send a message to the same computer? Well, then we will have to run a single-source algorithm again. To eliminate this cost we can have one of the computers (that will be elected during a voting-like process) calculate the shortest paths from all to all vertices using an all pair shortest path algorithm and send this information to all the other computers. This way all the computers know which is the fastest path to any other computer. Using this concept we need to make sure that the path is existent and that no computer in between has been shut down and/or is not available. This topic has to do with Distributed and Parallel Systems that I will cover some time in the near future in our Networking category! :)
Floyd Warshall Algorithm:
The Floyd-Warshall algorithm is the simplest All Pair Shortest Path Algorithm that you can implement. The algorithm works with positive and negative Edge weights, but can't detect negative weight circles and so doesn't work with them at all. This algorithm compares all possible paths through the graph between each pair of vertices and so has a O(V^3) complexity that makes it slow with a large number of vertices.
Pseudocode from wikipedia:

You can see that we have to use a matrix to store the distances calculated and first initialize the matrix to the adjacency matrix of the graph and then check all the possible paths with 3 "stacked" for loops! We will use the same pseudocode, but tweak it a little bit to suit our needs.
Floyd Warshall Java Implementation:
To implement this Algorithm we will use the adjacency matrix implementation of our basic graph. We will change the boolean adjacency matrix to an float matrix to store the weights and initialize these weights to infinity (or the maximum float number). We then first initialize the distance matrix of the algorithm to equal the adjacency matrix. We then loop through all vertices one by one in a triple for loop and check the condition dist(i, k) + dist(k, j) < dist(i, j) and set the dist(i, j) equal to the left part if it's true. Printing is pretty simple, and to get rid of the giant floating number I will print INF if the distance is equal to this giant floating number that we called infinity.
So, our Graph class looks like this:
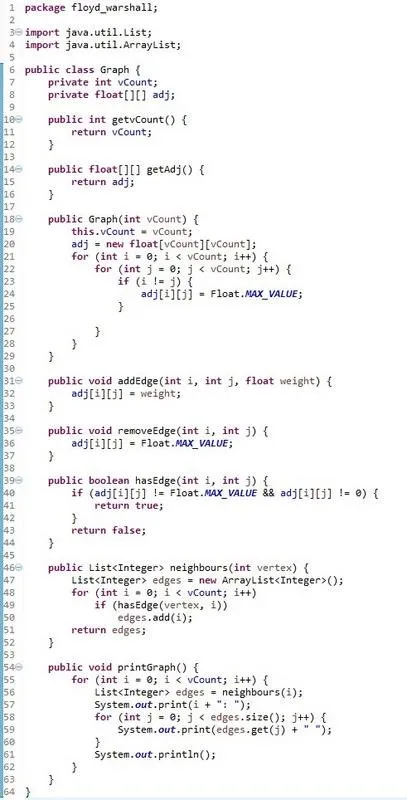
The TestGraphs class that also contains the Algorithm looks like this:
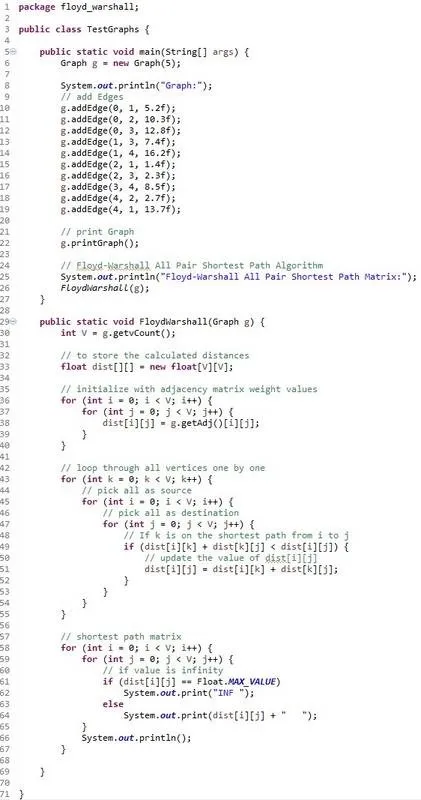
Running the last class we will see the Console print out the results as following:

You can get the codes in the following pastebin links:
Don't forget to remove the package declaration or put the classes inside of a package with that name.
Johnson Algorithm:
So, what is Johnson's Algorithm? Well Johnson's Algorithm combines the Dijkstra and Bellman-Ford Algorithms for Single-Source Shortest Paths to solve the All-Pair Shortest Path Problem. The algorithm first adds a new Node/Vertex to the Graph that is connected to all the others with zero-weight. It then uses the Bellman-Ford Algorithm on that newly added node to find the shortest paths from this node (actually from all the other nodes, because of the zero-weight) to all the other nodes, by also detecting negative-weight circles that will make the algorithm terminate. The algorithm then re-weights the original Graph by using the calculated distances (it removes the negative weights to prepare the graph for Dijkstra) and finally, after removing the added vertex, uses Dijkstra's algorithm to find the shortest paths from each node to every other node in the re-weighted graph.
This algorithm is slightly faster then the Floyd-Warshall algorithm and also detects negative circles, something that the first couldn't do. The problem is that this algorithm depends on the other two algorithms and so the implementation becomes much more complex. We already talked about Dijkstra and Bellman-Ford, but the implementation I made was simple so that everybody can understand it. This means that if we put this algorithms in use (after tweaking them a little bit) with Johnson's algorithm we will not get the best possible performance!
I will not implement the algorithm and leave it to you. You already know what the algorithm does and I also implemented the two algorithm that this algorithm needs in previous posts. So, if you find a pseudocode online you can actually make it happen pretty fast. Have fun! :P
And this is actually it for today!
Next time in Java Graphs we will talk about the Maximum Flow problem and the Ford-Fulkerson algorithm that is mainly used to solve it!
Bye!
