Until I upload the Java Exercise Solution we will be taking a look into C again. Today's post will be about Recursive Algorithms in C Language, but it will also work in mostly every language, cause the most use C-like syntax. So, let's start out.
Recursion:
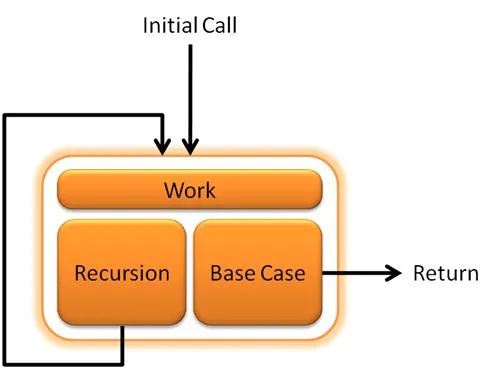
We use a recursion when we want to solve a problem by using smaller instances of the same problem. So a recursive function will call itself to solve a part of the problem. We could split the problem in half everytime (divide-and-conquer) or simply decrease it by a factor (decrease-and-conquer). There are many recursive algorithms out there that are faster than non-recursive algorithms, but sometimes a recursion could bring a dramatic drop in the performance and increase the complexity of the Algorithm.
A simple layout of an recursion is this:
return_type function_name(//parameters){
if (//stop condition)
return value;
else
return function_name(//other parameters); //it could also be opposite way
} Beware that not all recursive algorithms need to return a value, but parameters are needed to specify the "size" of the new subproblem.
Example 1:
The best example for recursion I think is the calculation of a Factorial or natural number. A Factorial is the number n! that represents the multiplication of all natural numbers from 1 until n (1*2*...*n). From the Math behind the Factorial we know that n! = n * (n - 1)! and so we will create a recursion problem that uses exactly this. If you don't know yet the Factorial of 0 is 1.
The Code is the following:
long int factorial (int n){ // it will first start out going downwards up to 0 if(n >= 1){ //we return the value of n * (n - 1)!, // where the second one gets the value when we reach 0 return n * factorial(n - 1); //recursion } else{ // when it reaches 0 it stop the recursion and starts going back // by multiplying 1*2*...*n and at the end return our value return 1; }}This algorithm uses the Decrease-and-Conquer method of Recursion. Let's take a look into a Divide-and-Conquer one.
Example 2:
An easy algorithm that uses it is the binary search algorithm that find a number inside of an sorted array in the most efficient way possible. It splits the problem in half by going only to left or right side checking if the number in the middle of this problems array is smaller or greater than the number we are searching for.
So, if the Array is A (3, 5, 8, 9, 11, 15) and we want to find 11 we will do the following:
middle = 6/2 = 3 and A[3] = 9 < 11 so we look in the right side. A(11, 15)
middle = 2/2 = 1 and A[1] = 15 > 11 so we look in the left side. A(11)
11 = 11 found
But we don't create new Arrays but use left and right indicators for the region in the Array we are in.
The Code looks like this:
int binary_search(int A[], int left, int right, int value){ if(left == right){ // check if 1 value in Array // if it is the value if(A[left] == value){ return left; // return index } else{ return -1; // return not found index } } else if(left > right){ // end condition return -1; // return not found index } int middle = (left + right)/2; // find middle // if middle is the value if(A[middle] == value){ return middle; // return index of middle } else if(A[middle] > value){ // smaller return binarysearch(A, left, middle, value); } else{ // greater return binarysearch(A, middle + 1, right, value); }}We return the index cause this is the correct way of doing it and then after calling the function we check if it is -1 to say it was not found and else print or save the index it was found.
I only did this post to make sure that everyone has an idea of what an recursive algorithm is and does, because the next posts will be about Lists and Trees that need recursive algorithms (we can do it also without, but it is better to do it with to make things "easier").
