In this Post we will take a look at more Advanced Tree Structures. We already talked about an basic Binary Tree using C Language here. Today, we will expand that Code to create an AVL Tree and we will also take a look at how an Red-Black and 2-3 Tree works. We use all of them to prevent having an unbalanced tree that has a bad average access time. So, without further do, let's get started!
Quick Recap:
In our Binary Tree Post we defined our Tree as a struct that contains Data and two pointers to the left and right Item, like this:
typedef struct TNode{ //DATA struct TNode *left; struct TNode *right;}TNode;
The AVL Trees will use the exact same schema, cause they are Binary Trees that have some kind of sorting that self-balances the Tree, so that the average access time is minimum.
Our new TreeNode used in AVL Trees we will use the same basic Code:
TNode *nn;nn = (TNode*)malloc(sizeof(TNode));// for every Data Variable we donn->val = val;// we set the pointers to NULLnn->left = NULL;nn->right = NULL;And we will search, print and find the successor in the same exact way we did in an Basic Binary Tree like this:
TNode* search(TNode *root, int val){ // if empty or found at root if(root == NULL || root->val == val){ // return root return root; } // if smaller else if(val < root->val){ // call function again for left side return search(root->left, val); } // if greater else if(val > root->val){ // call function again for right side return search(root->right, val); }}void preorder(TNode *root){ if(root == NULL) return; printf("%d ", root->val); if(root->left != NULL)inorder(root->left); if(root->right != NULL)inorder(root->right);}void inorder(TNode *root){ if(root == NULL) return; if(root->left != NULL)inorder(root->left); printf("%d ", root->val); if(root->right != NULL)inorder(root->right);}void postorder(TNode *root){ if(root == NULL) return; if(root->left != NULL)inorder(root->left); if(root->right != NULL)inorder(root->right); printf("%d ", root->val);}TNode* successor(TNode *node){ TNode *cur; // set cur to point to our node cur = node; // find the most left child while(cur->left != NULL){ // set cur to left pointer cur = cur->left; } // it returns the most left child return cur;}
Things will change in the process of Insertion and Deletion, cause we will have to make sure that some Conditions are met and if they don't we will have to "fix" our Tree using some Rotation functions!
AVL Trees:
An AVL Tree is an self-balancing binary search Tree, where the heights of the 2 sub Trees of any Node differ by at most one. This way our Tree will never become an Left or Right-Only Child Tree, but the Tree will use Rotation functions that will bring the Tree back in balance if it is not. So, our Tree Node struct will now contain also a height variable to make things easier.
The Code looks like this:
typedef struct TNode{ int val; int height; struct TNode *left; struct TNode *right;}TNode;We will use an function that returns the height of an TNode or 0 if it doesn't exist so that we can find the maximum height (using an max function) of the 2 childs of a specific Node. Afterwards, using an balance function that calculates the difference we can check if our Tree is out of balance.
The Code looks like this:
int max(int a, int b){ return (a > b)? a : b;}int height(TNode *N){ if (N == NULL) return 0; return N->height;}int getBalance(TNode *N){ if (N == NULL) return 0; return height(N->left) - height(N->right);}To insert a new Node or delete an existing on in the Tree we do it the same way we did in normal Binary Trees and afterwards we check if our Tree lost it's balance. Then we would have to re-balance it using Rotations.
There are 4 Rotation Cases that can happen. Those are (and can be solved using):
- Left-Left Case (right rotation)
- Left-Right Case (left and then right rotation)
- Right-Right Case (left rotation)
- Right-Left Case (right and then left rotation)
So, we have to write a Code that rotates a Node right and one that rotates a Node left.
TNode *rightRotate(TNode *y){ TNode *x = y->left; TNode *z = x->right; // Perform rotation x->right = y; y->left = z; // Update heights y->height = max(height(y->left), height(y->right))+1; x->height = max(height(x->left), height(x->right))+1; // Return new root return x;}TNode *leftRotate(TNode *x){ TNode *y = x->right; TNode *z = y->left; // Perform rotation y->left = x; x->right = z; // Update heights x->height = max(height(x->left), height(x->right))+1; y->height = max(height(y->left), height(y->right))+1; // Return new root return y;}So, our Insertion and Deletion Functions now look like this:
TNode* insert(TNode *node, int val){ // normal BST insertion TNode *nn; nn = (TNode*)malloc(sizeof(TNode)); // for every Data Variable we do nn->val = val; // height of nn is initialized as 1 nn->height = 1; // we set the pointers to NULL nn->left = NULL; nn->right = NULL; // check if tree is empty if(node == NULL){ // return nn as our new node or // because of recursion it will set // the nn were it belongs in the tree return nn; } if(val < node->val){ // call function again for left side node->left = insert(node->left, val); } else if(val > node->val){ // call function again for right side node->right = insert(node->right, val); } else{ // equal (don't insert) return node; } // update height node->height = 1 + max(height(node->left), height(node->right)); // get the balance factor int balance = getBalance(node); // Left Left Case if (balance > 1 && val < node->left->val) return rightRotate(node); // Right Right Case if (balance < -1 && val > node->right->val) return leftRotate(node); // Left Right Case if (balance > 1 && val > node->left->val){ node->left = leftRotate(node->left); return rightRotate(node); } // Right Left Case if (balance < -1 && val < node->right->val){ node->right = rightRotate(node->right); return leftRotate(node); } // return unchanged return node; }TNode* delete(TNode *node, int val){ // standard BST deletion // check if tree is empty if(node == NULL){ printf("Not found!\n"); return node; } if(val < node->val){ // call function again for left side node->left = delete(node->left, val); } else if(val > node->val){ // call function again for right side node->right = delete(node->right, val); } else{ // when val was found (cases) // has left and right child if(node->left != NULL && node->right != NULL){ // find successor TNode *s = successor(node->right); // set value of Node to be deleted to successor's value node->val = s->val; // delete successor node->right = delete(node->right, s->val); } // has only left child else if(node->left != NULL){ // set node to it's child node = node->left; } // has only right child else if(node->right != NULL){ // set node to it's child node = node->right; } // has no child else{ // simply set node to be deleted to NULL node = NULL; } } // if empty simply return if (node == NULL) return node; // update height node->height = 1 + max(height(node->left), height(node->right)); // get the balance factor int balance = getBalance(node); // Left Left Case if (balance > 1 && val < node->left->val) return rightRotate(node); // Right Right Case if (balance < -1 && val > node->right->val) return leftRotate(node); // Left Right Case if (balance > 1 && val > node->left->val){ node->left = leftRotate(node->left); return rightRotate(node); } // Right Left Case if (balance < -1 && val < node->right->val){ node->right = rightRotate(node->right); return leftRotate(node); } // return unchanged return node; }Red-Black Trees:
Red-Black Trees use a similar concept. When inserting and deleting frequently the rotations in AVL Trees cost time and that is when Red-Black Trees become useful. Some Basic Conditions are that:
- Every Node is Red or Black colored (variable color)
- The Root is Black always
- There can't be to Adjacent Red Nodes (Red Node can't have Red Parent or Child)
- Every path from the root to a NULL node must have the same number of black nodes.
Using this concept the Tree remains balanced, because of the recoloring and the rotation of the Nodes.
Now, let's take a look at the recoloring and rotation process. When inserting or deleting we do it the exact same way we did in normal binary Trees and afterwards we will first try to recolor our Nodes and if it doesn't solve the problem we afterwards rotate (that's why we save rotations). The new Node inserted is always Red and the algorithms depend upon the color of the uncle of this newly inserted Node. If the uncle is red we do recoloring and if the uncle is black we do rotations and/or recoloring.
So, we have this Cases:
- If the newly inserted Node is the root (first Node inserted) we change it's color to black
- If parent and uncle are Red we change the color of parent and uncle to black, color of grandparent to red and continue on by setting the grandparent's grandparent to red and his grandparent to red and so on..
- If parent is red and uncle black we we do the same 4 Cases of AVL Trees (RR, RL, LR, LL)
The first 2 do recoloring and the last one is for rotations. So, the rotations are the exact same we had in AVL Trees, but we also have colors and have to check the Colors, cause they could prevent rotations and we would only need recoloring.
Writing this Code in C is pretty difficult, cause it will contain parent Nodes and stuff, so it is preferable to write it in an Object-Oriented Language like C++, C# or even Java. We also only talked about inserting, removing, rotating, recoloring and all that stuff directly with pseudocode on a Tree graphically in my University. We don't did any specific language implementation. I searched a little bit and I found this website that explains red-black trees pretty well in C++. If you are interested take a look.
2-3 Trees:
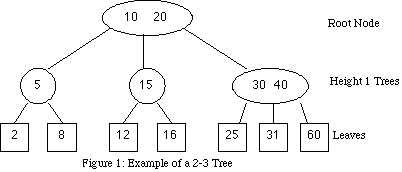
A 2-3 Tree is a Tree where each Node has 2 children and one data element (2-Node) or 3 children and two data elements (3-Node). So, we now don't have left and right only, but also a center child sometimes. This Trees are also balanced cause the left, center and right subtree contain close to the same amount of data.
A 2-3 Tree has this Properties:
- Every Node is a 2-Node or 3-Node
- All leaves are at the same level
- All data is kept in sorted order
We don't did any Language Implementation in our University. But, we learned how to do function like insert, delete, search on an 2-3 Tree using pseudocode and doing those functions by hand on a Tree graphically (the same way we did it in Red-Black Trees). It again is much easier to create such Code in an language that is Object-Oriented like C++. I Found a pdf Online that explains it using pseudocode. You can use this pseudocode to implement it in any language you like. Here the link.
This was the end of today's Post. I only wanted to explain the AVL Trees using C Code, cause they are also much easier then the other 2. We only had to expand our Code a little to set it up for AVL Trees and I think it's preferable to use an AVL Tree instead of an normal BST, to keep the Tree balanced and the access time fast. I wanted to explain the concept of the other 2, cause it is interesting to know that there are such things and if someone wants to implement something difficult in a specific language for practice an Red-Black or 2-3 Tree is something worth looking for.
Hope you enjoyed it!
Thanks :)
