
Image source: https://circuitglobe.com/what-is-self-inductance.html
Introduction
Hello it's a me again Drifter Programming! Today we continue with Electromagnetism to get into Self Induction, that we already mentioned last time! So, without further do, let's get straight into it!
Self Induction
Last time we saw how the magnetic field of a coil affects another adjacent coil causing the effect of Mutual Induction that induces a current on the second coil that tries to oppose the magnetic flux change caused by the first coil. Another very important form/type of Inductance is the so called Self Induction. Self Inductance is exactly what you think it is! It's the effect that a single coil experiences by the magnetic flux change caused by itself. Under the effects of self inductance an EMF or electro-motive force in that same wire or coil, producing what is often termed a back-EMF, is being produced. The effect is noticed in the same wire or coil that generated the magnetic field that caused the induction and so that's why this effect is known as self inductance. It's the phenomenon in which a change in electric current in a circuit produces an induced electro-motive-force in the same circuit.
Self Inductance's SI unit, the same way as Mutual Inductance, is the so called Henry (H) which is equal to 1Vs/A and geometrical unit (has no vector variables in it).
Let's explain this phenomenon a little better...by also getting into actual useful equations!
We know that when a current is passing through a conductor, and especially through a coil or inductor a magnetic field is being induced. The generated magnetic field extends outwards from the wire or inductor and couples with other circuits, but also with the circuit from which it is set up. The magnetic field can be expressed as concentric loops of magnetic flux that surround the wire. This loops join up with others from other loops of the same coil and enable a self-coupling within the coil. Therefore, when the current in a coil change, this causes a voltage to be induced in the different loops of the coil (Self-inductance).
That way from Mutual Induction we know that the induced voltage is:

Where:
- VL is the induced voltage (emf)
- N is the number of turns in the coil
- dφ/dt is the rate of change of magnetic flux
Using the inductance and rate of change of current, the induced voltage can also be expressed as:
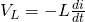
Lenz's law and Self Inductance
Lenz's law states that the current induced in a circuit due to a change or a motion in a magnetic field is so directed as to oppose the change in flux and to exert a mechanical force opposing the motion.
The phenomenon of self inductance can be defined as a property that a coil has due to which it opposes the change of the current flowing through it. If the current in the coil is increasing, the self-induced emf produced in the coil will oppose the rise of current, that means the direction of the induced emf is opposite to the applied voltage (Lenz's law again). If the current in the coil is decreasing, the emf induced in the coil is in such a direction as to oppose the fall of current, which means that the direction of the self-induced emf is same as that of the applied voltage. Self-inductance does not prevent the change of current, but it delays the change of current flowing through it.
It's worth noting that this property only opposes changing current and doesn't affect steady current (direct current) that is flowing through it.
Inductance of a Coil
We covered a lot till now, but not how to calculate the Inductance L!
By increasing the number of loops or turns within a coil, increasing the magnetic flux or decreasing the current, we increase the Self-inductance (L) of a coil. As an equation this looks like this:

Where:
- L is the Self Inductance
- N is the number of turns
- Φ the magnetic flux
- I the current
The product NΦ is also called magnetic flux linkage and so this expression can also be defined as the magnetic flux linkage divided by the current. Effictively the same magntitude if current flows through each turn of the coil. But, note that this equation can only be applied on linear magnetic materials!
Let's now consider a long solenoid coil with N number of turns per meter length.
The magnetic field around such a solenoid is:

Therefore, the magnetic flux is:

From all this the Inductance of a air cored solenoid is:

If the inner core is made of some ferromagnetic material such as soft iron, cobalt or nickel, the inductance of the coil would greatly increase because for the same amount of current flow the magnetic flux generated would be much stronger. By including the relative permeability of such a material we get:

which is the final equation for the inductance of a coil!
REFERENCES:
- https://www.electronics-notes.com/articles/basic_concepts/inductance/self-inductance-lenzs-law.php
- https://circuitglobe.com/what-is-self-inductance.html
- https://www.radio-electronics.com/info/formulae/inductance/self-inductance.php
- https://www.electronics-tutorials.ws/inductor/inductance.html
Mathematical equations that I had in this post where drawn using quicklatex!
Previous posts about Electromagnetism
Electric fields:
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
Electric flux:
Electric flux and Gauss's law -> Electric flux, Gauss's law
Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications
Applications of Gauss's law (part 2) -> more Gauss applications
Electric flux exercises -> examples in electric flux and Gauss's law
Electric potential:
Electric potential energy -> explanation of work-energy, electric potential energy
Calculating electric potentials -> more stuff about potential energy, potential, calculating potentials
Equipotential surfaces and potential gradient -> Equipotential surface, potential gradient
Millikan's Oil Drop Experiment -> Millikan's experiment, electronvolt
Cathode ray tubes explained using electric potential -> cathode ray tube explanation
Electric potential exercises (part 1) -> applications of potential
Electric potential exercises (part 2) -> applications of potential gradient, advanced examples
Capacitance:
Capacitors (Condensers) and Capacitance -> Capacitors, capacitance, calculating capacitance
How to solve problems around Capacitors -> combination, solving problems, simple example
Electric field energy and density -> Electric field energy, energy density
Dielectric materials -> Dielectrics, dielectric constant, permittivity and strength, how to solve problems
Electric capacitance exercises -> examples in capacitance, energy density and dielectrics
Current, resistance and EMF:
Electric current -> Electric current, current density
Electrical resistivity and conductivity -> Electrical resistivity, conductivity, thermal coefficient of resistivity, hyperconductivity
Electric resistance -> Resistance, temperature, resistors
Electromotive Force (EMF) and Internal resistance -> Electromotive force, internal resistance
Power and Wattage of Electronic Circuits -> Power in general, power/wattage of electronic circuits
Electric current, resistance and emf exercises -> exampes in all those topics
Direct current (DC) circuits:
Resistor Combinations -> Resistor combinations, how to solve problems
Kirchhoff's laws with applications -> Kirchhoff's laws, how to solve problems, applications
Electrical measuring instruments -> what are they?, types list, getting into some of them, an application
Electronic circuits with resistors and capacitors (R-C) -> R-C Circuit, charging, time constant, discharging, how to apply
RC circuit exercises -> examples in Kirchhoff, charging, discharging capacitor with/without internal resistance
Magnetic field and forces:
Magnetic fields -> Magnetism, Magnetic field
Magnetic field lines and Gauss's law of Magnetism -> magnetic field lines, mono- and dipoles, Flux, Gauss's law of magnetism
The motion of charged particles inside of a magnetic field -> straight-line, spiral and helical particle motion
Applications of charged particle motion -> CERN, Cyclotrons, Synchrotrons, Cavity Magetron, Mass Spectrometry and Magnetic lens
Magnetic force applied on Current-Carrying Conductors -> magnetic force on current-carrying conductors/wires, proofs
Magnetic force and torque applied on current loops (circuits) -> magnetic force on current loops, magnetic moment and torque
Explaining the Physics behind Electromotors -> tesla, history and explaining the physics behind them
Magnetic field exercises -> examples in magnetic force, magnetic flux, particle motion and forces/torque on current-carrying conductors
Magnetic field sources:
Magnetic field of a moving charged particle -> moving charge, magnetic field, force between parallel charged particles
Magnetic field of current-carrying conductors -> magnetic field of current, Biot-Savart law
Force between parallel conductors and the magnetic field of a current loop-> force between parallel conductors, magnetic field of current loop
Ampere's law and Applications -> Ampere's law, applications
Magnetic materials -> Magnetic materials, classification and types, material examples
Displacement current -> Displacement current, Extension of Ampere's law
Exercises in Magnetic field sources -> examples all around magnetic field sources
Electromagnetic Induction:
Electromagnetic Induction and Faraday's law -> Electromagnetic Induction, Experiments, Faraday's law
Motional Electromotive Force (Emf) -> Motional Emf, Faraday's law and motional emf, generalization
Lenz's law and Induced Electric fields -> Lenz's law, Induced Electric Fields
Eddy Currents and Applications -> Εddy currents, applications (brakes, testing, others)
Maxwell's equations -> What they are, each equation analyzed separately
Electromagnetic Induction exercises -> examples all around Electromagnetic Induction
Mutual and Self Induction:
Mutual Inductance -> Mutual Inductance, applications
And this is actually it for today's post! Next time in Physics we will get into Magnetic Energy...
C ya!
