Physics - Electromagnetism

Image source:

Introduction

Hello it's a me again Drifter Programming! Today we continue with Electromagnetism to get into Resistor-Inductor (R-L) circuits. I highly suggest you to go read my articles about Resistors and Inductors, cause else this article will be a whole lot of non-sense :P So, without further do, let's get started!

Energizing of a R-L circuit

Until now in this series we only covered circuits containing Resistors, Capacitors and both together (the so called RC circuits). By including the concept of inductance caused by an Electromagnetic Induction in inductors, which are mostly Coils that are being affected by Self-Induction, we can start combining those Inductors with Resistors, Capacitors and both to see how such circuits behave. Having an Inductor alone doesn't make sense anyway, cause in the "real world" all the coils (solenoids, relays etc.) will have some form of resistance. All components have a certain amount of resistance. That's why we will start talking about R-L or L-R Circuits which are circuits that contain Inductors and Resistors and so some Indutance L and a resistance R. Of cousre all this will be discussed for DC current, cause AC current is not yet been discussed...

Let's consider a series RL circuit, where a coil and a constant voltage source V are connected in serial. The coil of course has some resistance R and a inductance L. Those two components are separated by a switch which at first is open ("no voltage"). Let's say that we close the switch at time t = 0. Of course a current I now starts to flow through the circuit. But, the current doesn't rise to it's maximum value of V/R (Ohm's law) directly! The self induced emf caused by the Self Induction in the Coil is limiting the increase of current and therefore magnetic flux in the Coil (Lenz's law). After some amount of time passes the self induced emf and current are being reduced to zero and the current I in the circuit becomes constant (when it reaches the maximum value), where we can say that the circuit has been energized.

Applying Kirchhoff's Voltage Law (KVL) we can define the individual voltage drops in the circuit and find an expression for the current that flows through the circuit! KVL gives us:

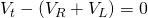
where:

Vt is the voltage in a specific time
VR the voltage drop caused by the resistor
VL the voltage drop caused by the inductor's emf

From Ohm's law we know that VR is:

The emf in the inductor is given by:

Therefore:

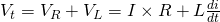
The voltage drop across the resistor depends upon the current I that flows through the current, while the voltage drop across the inductor depends upon the rate of change of the current (di/dt). For t = 0 the circuit has no current flow and so the total voltage is zero. As a first-order differential equation this can be proven to give the following current as a function of time:

Where:

V/R is sometimes noted as I0 or Imax, being the maximum current
e is the natural logarithm = 2.71828...
R is the resistance
L the inductance

The opposition of the inductor L is greater at the beginning, because the amount of change in the current/flux is greater. The opposition in form of induced emf decreases to zero as the current approaches its final value.

The power in the circuit is given by P = VxI, which for R-L series circuits get's the final form:

The first term (I^2R) is representing the power dissipated by the resistor in heat. The second term represents the power "absorbed" by the the inductor in form of magnetic energy.

The voltage with time in the inductor is defined as:

where ε is the maximum voltage that can be "provided" by the voltage source.

De-energizing of a R-L circuit

After fully energizing/charging the circuits, let's now open the switch or "remove" the constant voltage source V in some way. This is mostly done through another switch which creates another "smaller" circuit that doesn't contain the voltage source, but still connects the other components (the coil with resistance and inductance) in serial. By applying KVL again we now get:

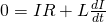
Where:

IR is the voltage drop in the resistor
L di/dt the voltage drop caused by the induced emf in the inductor

Solving this differential equation using calculus we end up with the following expression that gives us the current as a function of time:

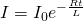
Of course when "disconnecting" the battery / voltage source from the circuit the current start dropping because energy is dissipated by the resistor. But, as we can see this is again not instantaneous, cause the inductor opposes the decrease by inducing an emf that tries to increase the current again. As we saw last time the amount of energy stored in a inductor is:

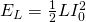
where I0 is now the maximum value of current that we reach.

The power dissipation rate is again I^2R and now the inductor is "acting" like a voltage source. When de-energizing the voltage provided by the inductor is given as:

(positive sign instead)

Characteristic time constant

The Time Constant (τ) in a series LR circuit is given as:

Using this value we can approximately calculate the time needed to reach the maximum or steady state current value. After 5τ seconds the inductance of the coil is considered to be zero and so effectively removed by the circuit, giving the maximum current I = V/R. The current at this point is only limited by the resistance of the resistor R.

A very interesting diagram is the following:

Image source: https://www.electronics-tutorials.ws/inductor/lr-circuits.html

Using this diagram of so called transient curves we can calculate the current at specific times as percentages of the maximum value.

When energizing:

at t = 0 -> no current
at t = τ -> ~63% of max
...
at t = 5τ -> theoretically 100% of max

When de-energizing:

at t = 0 -> maximum current I0 = V/R
at t = τ -> ~37% of max
...
at t = 5τ -> theoretically no current

An interesting table with more accurate values can be found:

http://electricalacademia.com/basic-electrical/rl-circuit-time-constant-time-constant-of-rl-circuit/

which has the table and also examples that we will get into some articles later on...

REFERENCES:

Mathematical equations that I had in this post where drawn using quicklatex!

Previous posts about Electromagnetism

Electric fields:

Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization

Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples

Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines

Electric dipoles -> Electric dipole, torque, potential and field

Electric charge and field Exercises -> examples in electric charges and fields

Electric flux:

Electric flux and Gauss's law -> Electric flux, Gauss's law

Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications

Applications of Gauss's law (part 2) -> more Gauss applications

Electric flux exercises -> examples in electric flux and Gauss's law

Electric potential:

Electric potential energy -> explanation of work-energy, electric potential energy

Calculating electric potentials -> more stuff about potential energy, potential, calculating potentials

Equipotential surfaces and potential gradient -> Equipotential surface, potential gradient

Millikan's Oil Drop Experiment -> Millikan's experiment, electronvolt

Cathode ray tubes explained using electric potential -> cathode ray tube explanation

Electric potential exercises (part 1) -> applications of potential

Electric potential exercises (part 2) -> applications of potential gradient, advanced examples

Capacitance:

Capacitors (Condensers) and Capacitance -> Capacitors, capacitance, calculating capacitance

How to solve problems around Capacitors -> combination, solving problems, simple example

Electric field energy and density -> Electric field energy, energy density

Dielectric materials -> Dielectrics, dielectric constant, permittivity and strength, how to solve problems

Electric capacitance exercises -> examples in capacitance, energy density and dielectrics

Current, resistance and EMF:

Electric current -> Electric current, current density

Electrical resistivity and conductivity -> Electrical resistivity, conductivity, thermal coefficient of resistivity, hyperconductivity

Electric resistance -> Resistance, temperature, resistors

Electromotive Force (EMF) and Internal resistance -> Electromotive force, internal resistance

Power and Wattage of Electronic Circuits -> Power in general, power/wattage of electronic circuits

Electric current, resistance and emf exercises -> exampes in all those topics

Direct current (DC) circuits:

Resistor Combinations -> Resistor combinations, how to solve problems

Kirchhoff's laws with applications -> Kirchhoff's laws, how to solve problems, applications

Electrical measuring instruments -> what are they?, types list, getting into some of them, an application

Electronic circuits with resistors and capacitors (R-C) -> R-C Circuit, charging, time constant, discharging, how to apply

RC circuit exercises -> examples in Kirchhoff, charging, discharging capacitor with/without internal resistance

Magnetic field and forces:

Magnetic fields -> Magnetism, Magnetic field

Magnetic field lines and Gauss's law of Magnetism -> magnetic field lines, mono- and dipoles, Flux, Gauss's law of magnetism

The motion of charged particles inside of a magnetic field -> straight-line, spiral and helical particle motion

Applications of charged particle motion -> CERN, Cyclotrons, Synchrotrons, Cavity Magetron, Mass Spectrometry and Magnetic lens

Magnetic force applied on Current-Carrying Conductors -> magnetic force on current-carrying conductors/wires, proofs

Magnetic force and torque applied on current loops (circuits) -> magnetic force on current loops, magnetic moment and torque

Explaining the Physics behind Electromotors -> tesla, history and explaining the physics behind them

Magnetic field exercises -> examples in magnetic force, magnetic flux, particle motion and forces/torque on current-carrying conductors

Magnetic field sources:

Magnetic field of a moving charged particle -> moving charge, magnetic field, force between parallel charged particles

Magnetic field of current-carrying conductors -> magnetic field of current, Biot-Savart law

Force between parallel conductors and the magnetic field of a current loop-> force between parallel conductors, magnetic field of current loop

Ampere's law and Applications -> Ampere's law, applications

Magnetic materials -> Magnetic materials, classification and types, material examples

Displacement current -> Displacement current, Extension of Ampere's law

Exercises in Magnetic field sources -> examples all around magnetic field sources

Electromagnetic Induction:

Electromagnetic Induction and Faraday's law -> Electromagnetic Induction, Experiments, Faraday's law

Motional Electromotive Force (Emf) -> Motional Emf, Faraday's law and motional emf, generalization

Lenz's law and Induced Electric fields -> Lenz's law, Induced Electric Fields

Eddy Currents and Applications -> Εddy currents, applications (brakes, testing, others)

Maxwell's equations -> What they are, each equation analyzed separately

Electromagnetic Induction exercises -> examples all around Electromagnetic Induction

Mutual and Self Induction:

Mutual Inductance -> Mutual Inductance, applications

Self Induction -> Self Induction, Lenz's law, Inductance of a Coil

Magnetic Energy Density -> Energy stored in a magnetic field (or inductor), Magnetic energy density, Coaxial Cable Inductance Example

And this is actually it for today's post and I hope that you learned from it! Next time in Physics we will get into L-C (Inductor-Capacitor) circuits...

C ya!

Physics - Electromagnetism - R-L circuits