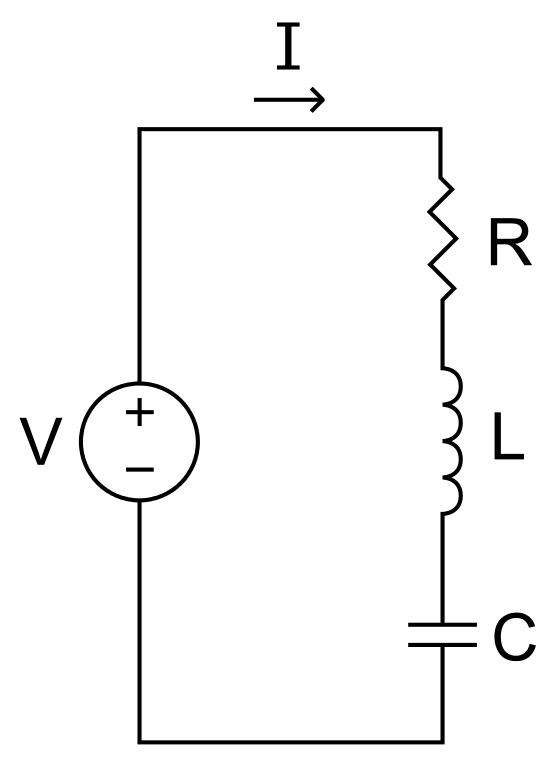
Image source: https://commons.wikimedia.org/wiki/File:RLC_series_circuit_v1.svg
Introduction
Hello it's a me again Drifter Programming! Today we continue with Electromagnetism to get into Resistor-Inductor-Capacitor (R-L-C) circuits! I highly suggest you to go and read stuff about the components which are the Resistors, Capacitors, Inductors, and also about the previous circuits that we covered: R-C circuits, L-C Circuits and R-L circuits...The most important has to be the previous article about L-C circuits. So, without further do, let's get started!
R-L-C circuit
Last time we talked about circuits that contain an inductor with inductance L and a capacitor with capacitance C. But, such a circuit is not feasible in real life, cause these components and even the wires that connect them together have some electrical resistivity. Considering that the total resistance R of a circuit is stored in one resistor we then define the so called Resistor-Inductor-Capacitor (R-L-C) circuits, which are closer to "real life". As with the previous circuits, we will again only get into the series connection of those three components. Connecting them in serial means that the current flowing through each element is equal to the total current I that is flowing through the circuit (serial -> same current, parallel -> same voltage).
Parallel circuits will be covered when we get into AC current.
In L-C circuits we saw that the energy from the capacitor was "moved" to the inductor and vise versa in an continuous oscillation of frequency ω. At each period of this oscillation the capacitor started out fully charged, was discharged, charged again in inverse polarity and discharged again by getting back to the initial position. During that time the inductor started out fully de-energized, was energized, de-energized again and then energized in inverse polarity, de-energizing one final time to get back to the initial non-energized position. No energy is lost or created in such a circuit and so the total energy remained the same. The energy just changed from electric to magnetic, and vise versa. By including a resistor component, energy in form of heat will start to "leave" the circuit. This means that the total energy of the circuit will decrease at each oscillation, until it reaches zero. The capacitor will have a smaller charge Q at each oscillation giving the capacitor less electric energy, whilst the current in the circuit will be smaller and smaller, decreasing the magnetic energy stored in the inductor. I'm of course talking about the max-points, where each of those components has the total energy of the circuit, but the total sum of energy at each given point of the oscillation of course decreases as well! From all this we can understand that we now have a damping oscillation.
Oscillation
Let's analyze this oscillation a little bit better...
Consider a series RLC circuit that contains a voltage source V. Applying KVL for this circuit we find that:

A very similar equation to the one of last time, where we now also consider the voltage drop across a resistor of resistance R that can be found using Ohm's law (V = IR).
By doing the Calculus needed (solving the differential equation etc.) we can find the final equation of the charge in the capacitor is:
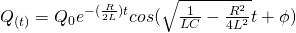
The coefficient of t is the so called oscillation frequency of a damping oscillation noted as ω':
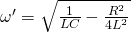
When R = 0 we of course get the oscillation frequency ω that we covered last time! As R is increasing the frequency becomes smaller and smaller. At the point where R^2 = 4L/C the subroot now gives zero and so the circuit isn't oscilatting at all (critical damping). If we increase the resistance R even more, the circuit will be over-damped and Q will now be calculated as the sum of two decreasing exponential functions!
A cool simulation can be found in the following link:
You can see how the individual voltages start dropping, until finally reaching zero.
Applications
RLC circuits are being used in many many applications. More specifically the Series RLC circuits that we covered today are used in:
- Variable tuner circuits
- Low pass, high pass, band pass and band stop filters
- Oscillators
- Voltage multipliers
- Pulse discharge circuits
We will get back to these circuits when we get into AC current, which is actually the next topic of Electromagnetism!
REFERENCES:
- https://www.electronics-tutorials.ws/accircuits/series-circuit.html
- https://circuitglobe.com/what-is-rlc-series-circuit.html
- http://people.seas.harvard.edu/~jones/es154/pages/nicetut/book4/RLC.html
Mathematical equations that I had in this post where drawn using quicklatex!
Previous posts about Electromagnetism
Electric fields:
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
Electric flux:
Electric flux and Gauss's law -> Electric flux, Gauss's law
Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications
Applications of Gauss's law (part 2) -> more Gauss applications
Electric flux exercises -> examples in electric flux and Gauss's law
Electric potential:
Electric potential energy -> explanation of work-energy, electric potential energy
Calculating electric potentials -> more stuff about potential energy, potential, calculating potentials
Equipotential surfaces and potential gradient -> Equipotential surface, potential gradient
Millikan's Oil Drop Experiment -> Millikan's experiment, electronvolt
Cathode ray tubes explained using electric potential -> cathode ray tube explanation
Electric potential exercises (part 1) -> applications of potential
Electric potential exercises (part 2) -> applications of potential gradient, advanced examples
Capacitance:
Capacitors (Condensers) and Capacitance -> Capacitors, capacitance, calculating capacitance
How to solve problems around Capacitors -> combination, solving problems, simple example
Electric field energy and density -> Electric field energy, energy density
Dielectric materials -> Dielectrics, dielectric constant, permittivity and strength, how to solve problems
Electric capacitance exercises -> examples in capacitance, energy density and dielectrics
Current, resistance and EMF:
Electric current -> Electric current, current density
Electrical resistivity and conductivity -> Electrical resistivity, conductivity, thermal coefficient of resistivity, hyperconductivity
Electric resistance -> Resistance, temperature, resistors
Electromotive Force (EMF) and Internal resistance -> Electromotive force, internal resistance
Power and Wattage of Electronic Circuits -> Power in general, power/wattage of electronic circuits
Electric current, resistance and emf exercises -> exampes in all those topics
Direct current (DC) circuits:
Resistor Combinations -> Resistor combinations, how to solve problems
Kirchhoff's laws with applications -> Kirchhoff's laws, how to solve problems, applications
Electrical measuring instruments -> what are they?, types list, getting into some of them, an application
Electronic circuits with resistors and capacitors (R-C) -> R-C Circuit, charging, time constant, discharging, how to apply
RC circuit exercises -> examples in Kirchhoff, charging, discharging capacitor with/without internal resistance
Magnetic field and forces:
Magnetic fields -> Magnetism, Magnetic field
Magnetic field lines and Gauss's law of Magnetism -> magnetic field lines, mono- and dipoles, Flux, Gauss's law of magnetism
The motion of charged particles inside of a magnetic field -> straight-line, spiral and helical particle motion
Applications of charged particle motion -> CERN, Cyclotrons, Synchrotrons, Cavity Magetron, Mass Spectrometry and Magnetic lens
Magnetic force applied on Current-Carrying Conductors -> magnetic force on current-carrying conductors/wires, proofs
Magnetic force and torque applied on current loops (circuits) -> magnetic force on current loops, magnetic moment and torque
Explaining the Physics behind Electromotors -> tesla, history and explaining the physics behind them
Magnetic field exercises -> examples in magnetic force, magnetic flux, particle motion and forces/torque on current-carrying conductors
Magnetic field sources:
Magnetic field of a moving charged particle -> moving charge, magnetic field, force between parallel charged particles
Magnetic field of current-carrying conductors -> magnetic field of current, Biot-Savart law
Force between parallel conductors and the magnetic field of a current loop-> force between parallel conductors, magnetic field of current loop
Ampere's law and Applications -> Ampere's law, applications
Magnetic materials -> Magnetic materials, classification and types, material examples
Displacement current -> Displacement current, Extension of Ampere's law
Exercises in Magnetic field sources -> examples all around magnetic field sources
Electromagnetic Induction:
Electromagnetic Induction and Faraday's law -> Electromagnetic Induction, Experiments, Faraday's law
Motional Electromotive Force (Emf) -> Motional Emf, Faraday's law and motional emf, generalization
Lenz's law and Induced Electric fields -> Lenz's law, Induced Electric Fields
Eddy Currents and Applications -> Εddy currents, applications (brakes, testing, others)
Maxwell's equations -> What they are, each equation analyzed separately
Electromagnetic Induction exercises -> examples all around Electromagnetic Induction
Mutual and Self Induction:
Mutual Inductance -> Mutual Inductance, applications
Self Induction -> Self Induction, Lenz's law, Inductance of a Coil
Magnetic Energy Density -> Energy stored in a magnetic field (or inductor), Magnetic energy density, Coaxial Cable Inductance Example
R-L circuits -> R-L circuit energizing, de-energizing, Characteristic time constant
L-C circuits -> L-C circuit, oscillations, energy cases, applications
And this is actually it for today's post and I hope that you learned from it! Without covering AC current, such circuits cannot be analyzed as in depth as the previous ones, but I still think that you got an overall idea. Next up in Physics are exercises/examples all around Mutual and Self Induction...including the 3 types of circuits that we talked about during the previous articles!
C ya!
