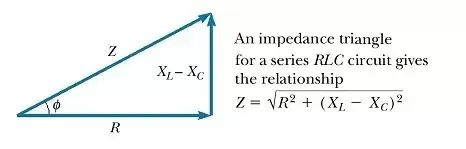
Image source: https://www.quora.com/What-is-the-Impedance-Triangle
Introduction
Hello it'a me again @drifter1! Today we continue with the Electromagnetism series to talk about the Power in AC circuits. To understand this article you should know things about power that you can find in my article: "Power and Wattage of Electronic Circuits". The previous article about Impedance might also be useful. I will of course make a small refreshment of all that knowledge, but still an article is an article. So without further do, let's get straight into it!
DC Resistive circuit
Let's start out with the "easy" DC power. The power consumed in DC circuits is simply the product of DC voltage times DC current. The metric of power in SI is the watt (W). The reactive components of capacitance and inductance don't affect the circuits consumption with DC current/voltage. As you might remember Electrical power is the "rate" at which electrical energy is being converted into heat. Of course Electrical power in general can be time-varying. The power at any instant of time is called instantaneous power and calculated by (with the help of Ohm's law):
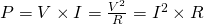
where:
- V is of course the DC voltage
- I the DC current
- R the total resistance of the circuit
From all these we can see that power only "exists" when both voltage and current are present, which is true for open-circuits, but also closed-circuit conditions as we will see in AC circuits!
Power in AC circuits
For AC circuits Electrical Power is still is a product of current and voltage. But, now the current and voltage are time-varying, following a sinusoidal waveform. This means that the instantaneous current and voltage are not constant, but constantly changing influenced by the oscillation of the supply signal. Therefore, the instantaneous power is also time-varying. Power in such circuits has not the same notion as before, but still P = VxI.
AC circuits have a change in current/voltage and therefore are being affected by the reactance of their capacitive and inductive components. Having such components electric fields and/or magnetic fields are being created/produced by these components, storing and returning back power to the circuit. So, what makes sense in such circuits is the average power absorbed, stored and returned over one complete cycle or period. The phase differences of current and voltage along the components/elements of AC circuts will make the equations of instantaneous power and average power much more complex..
Resistive:
Let's start of with plain resistive AC circuits that don't have any reactance...
Having no capacitive or inductive reactance, only the resistance of the resistor affects the circuit. This means that the resistor is the only component consuming energy. As we already know, the energy consumed in a resistor is equal to the voltage V across the component (equal to the power supplies voltage) times the current flowing through it. The current and voltage in resistors are in-phase and therefore:
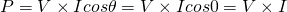
which is the exact same equation as before, but note that the current and voltage still change over time, meaning that the power is within a range of a maximum negative value and maximum positive value. Including the RMS values of Voltage and Current we then get the Average or Effective Power as:

Reactive:
Let's now get into purely reactive circuits, starting of with inductive circuits...
Purely inductive circuits have a voltage and current which are out-of-phase by a phase difference of 90 degrees. While the voltage applied to the inductor is changing, a self induced emf is being produced by the coil to oppose and limit the change in current flowing in the coil (Self Induction). Of course the "back" emf current cannot increase immediatly in-phase, but causes a small "lagging" behind of current behind voltage. The current stays behind by 90 degrees.
The real power in a pure inductor (with no resistance) is:
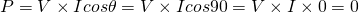
No actual power! This makes sense, cause inductors do not consume or dissipate any real or true power! This "imaginary" defined power is sometimes being called Reactive power.
In the same way purely capacitive circuits have no resistance. The current in such circuits leads over the voltage by 90 degrees, cause capacitors store electrical energy inside of their electric field directly. Again no heat is being dissipated, but only being stored "temporarily" inside of the capacitor.
Doing a similar calculation as before we now get:
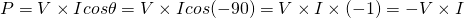
Seeing the negative sign you first might say that the capacitor produces energy. But, what it actually does is that it returns the energy back to the supply. During a full-cycle of voltage oscillation a "negative" current is being produced by the capacitor, which explains the negative sign. The capacitor simply returns the energy given to it in form of electrical energy and therefore the reactive power doesn't perform any real work.
Power Factor
To get into "mixed" circuits that are both resistive and reactive we shoulf first talk about the Power Factor and Power Triangle. Last time we already talked about impedance, which is a quantity that describes the combined effect of resistance and reactance in AC circuits. Getting into the Complex number space we can create the so called Impedance Triangle that I had in the beginning of this article.
The Real power of AC circuits is simply P = I^2R and all the other forms that we get from Ohm's law. The other forms of power, thinking about reactance as a "form" of resistance are:
- Reactive power -> Q = I^2X
- Apparent Power -> S = I^2Z
Reactive power is the power being stored and returned back to the circuit by the reactive components of capacitance and inductance. Apparent power includes the total effect of all the components (resistive and reactive). You can clearly see that Apparent power is the product of current squared times Impedance Z.
Real power can also be defined using the effective RMS voltage and current, which gives us the average power through-out a full cycle/period. Reactive power depends on the frequency/period of the voltage's oscillation, but can also be denoted as:
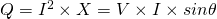
again including the RMS voltage, but having a phase difference in the range of 0 to 90 depending on the reactive effect of inductance and capacitance.
The total power in AC circuits that we call Apparent power is equal to:
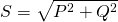
that we get by the Power triangle using Pythagora's theorem.
By power factor we mean the term cosθ that can be expressed in terms of circuit impedance or circuit power. The power factor is therefore equal to the quotient of real power (P) with apparent power (S):
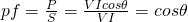
This factor therefore defines the phase angle/difference between the current and voltage waveforms. V and I are the magnitudes of the rms values of voltage and current.
Thinking in terms of power factor we can now saw that:
- The power factor in a purely resistive circuit is cos0 = 1.0 and so real power is equal to apparent power.
- The power factor in purely reactive circuits is cos90 = 0.0 and so the total power is zero, but there still is a voltage and current
- The power factor in mixed circuits is in the range: [0.0, 1.1]
So, to sum up:
- In a purely resistive circuit, all circuit power is dissipated by the resistor(s). Voltage and current are in phase with each other
- In a purely reactive circuit, no circuit power is dissipated by the load(s). Power is alternately absorbed from and returned to the AC source. Voltage and current are 90 degrees out of phase with each other.
- In a circuit consisting of resistance and reactance mixed, there will be more power dissipated by the load(s) than returned, but some power will definitely be dissipated and some will merely be absorbed and returned. Voltage and current in such a circuit will be out of phase by a value somewhere between 0 and 90 degrees.
REFERENCES:
- https://www.electronics-tutorials.ws/accircuits/power-in-ac-circuits.html
- https://www.electronics-tutorials.ws/accircuits/power-triangle.html
- https://www.allaboutcircuits.com/textbook/alternating-current/chpt-11/power-resistive-reactive-ac-circuits/
- https://electronicsarea.com/power-in-ac-circuits/
- http://hyperphysics.phy-astr.gsu.edu/hbase/electric/powerac.html
Mathematical equations that I had in this post where drawn using quicklatex!
Previous articles of the Electromagnetism series
Here we only have the previous two "chapters" and the current one....
Electromagnetic Induction:
Electromagnetic Induction and Faraday's law -> Electromagnetic Induction, Experiments, Faraday's law
Motional Electromotive Force (Emf) -> Motional Emf, Faraday's law and motional emf, generalization
Lenz's law and Induced Electric fields -> Lenz's law, Induced Electric Fields
Eddy Currents and Applications -> Εddy currents, applications (brakes, testing, others)
Maxwell's equations -> What they are, each equation analyzed separately
Electromagnetic Induction exercises -> examples all around Electromagnetic Induction
Mutual and Self Induction:
Mutual Inductance -> Mutual Inductance, applications
Self Induction -> Self Induction, Lenz's law, Inductance of a Coil
Magnetic Energy Density -> Energy stored in a magnetic field (or inductor), Magnetic energy density, Coaxial Cable Inductance Example
R-L circuits -> R-L circuit energizing, de-energizing, Characteristic time constant
L-C circuits -> L-C circuit, oscillations, energy cases, applications
R-L-C circuits -> R-L-C circuit, oscillation, applications
Mutual and Self Induction exercises -> examples all around Mutual and Self Induction
Alternating current:
Getting into Alternating current -> Phasor diagrams, Alternating current, Average (RMS) current and voltage, Differences, Advantages/Disadvantages
Electric Reactance in AC circuits -> Resistors, Inductor and Capacitor Reactance in AC circuits
Series R-L-C circuits Impedance -> Series R-L-C circuits, Phasor Diagrams, Impedance
Final words | Next time
And this is actually it for today's post! Next time we will get into the Resonance of Series R-L-C circuits and next up Parallel R-L-C circuits!


Keep on drifting!
