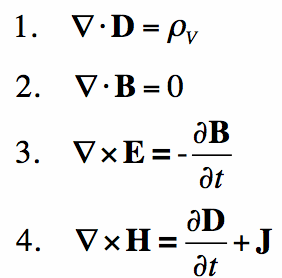
Image source: http://www.maxwells-equations.com/
Introduction
Hello it's a me again Drifter Programming! Today we continue with Electromagnetism to get into Maxwell's Equations. We already talked about them in other articles, but I think that making a whole article around them is not a bad idea! Of course a lot of "new" things will come into the game... So, without further do, let's get straight into it!
Maxwell's Equations - What they are
Maxwell's Equations are four equations that form a complete description of the production and interrelation of electric and magnetic fields. The previously established experimental laws and facts regarding electric and magnetic fields could be summed up in just these four equations, which we nowadays call Maxwell Equations. It was James Clerk Maxwell who unified them into a symmetric coherent set of Equations and that's why these four equations got his name. Maxwell's equations describe how electric charges and electric currents create electric and magnetic fields, and also how electric fields can generate magnetic fields and vise versa. Knowing and understanding Maxwell's equations you can understand anything in Electromagnetism!
The four equations are:
- Gauss' law
- Gauss's Magnetism law
- Faraday's law
- Ampere's law
These basic equations of electricity and magnetism can be used as a starting point for advanced courses, but are usually first encountered as unifying equations after the study of electrical and magnetic phenomena. Being laws/rules that the universe "obeys", we can use these equations to analyze the behavior of electric and magnetic fields. As we already know a flow of electric current produces a magnetic field. When this current flow also varies with time then the magnetic field will also give rise to an electric field (electromagnetic induction - a current/electric field is being induced).
Maxwell's equations require complicated math, but understanding them in a more intuitive level is not that difficult and so this is the approach that I will try to follow today.
Before getting into them I would like to give you a small list of the symbols that we will use in the equations and what these symbols are representing. The symbols and their units are:
- E -> electric field in N/C or V/m
- B -> magnetic field or magnetic flux density in Tesla οr Wb/m^2
- H -> magnetic field strength in A/m
- D -> electric displacement field in C/m^2
- Q or q -> electric charge in C
- ρ -> electric charge density in C/m^3
- I or i -> electric current in A
- J -> current density in A/m^2
- A -> area in m^2 (sometimes referred as surface S)
- V -> volume in m^3
- l or r -> path length in m
- v -> velocity in m/s
- ε -> permittivity in F/m (mostly the ε0 constant)
- μ -> permeability in N/A^2 (mostly the μ0 constant)
- σ -> conductivity in S/m
- ρ -> resistivity in Ωm (yes it's the same symbol...)
- c -> speed of light constant (3x10^8 m/s)
- k -> Coulomb's constant
A lot of "new" symbols are in this list!
After talking about all of them as a whole let's now get into each one separately to understand in which specific electromagnetic applications each equation is useful!
Equation 1: Gauss's Law
The first equation is simply Gauss's law (for electricity) and states that:
The electric flux through any closed surface is equal to the total charge enclosed by the surface, divided by εo.
Mathematically this looks like this:
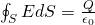
where S is a closed surface enclosing the charge Q.
Using charge density per unit of volume we can rewrite this equations as:

where V is the volume bounded by the surface S.
The differential form is:
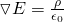
Using the "new" symbols this becomes:
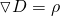
where:
- D = ε0E+P (general case)
- D = ε0E (free space)
- D= εE (isotropic linear dielectric)
This equation shows us that an electric field diverges from electric charges. This field is the result of Coulomb force (the force applied on charges from charges). As we know there are two types of charges, positive and negative. The force between like charges is repulsive, whilst the force between unlike charges is attractive. The electric field lines diverge from positive charges and converge on negative charges.
The equation is true in general and so in dynamic and static fields. Gauss' law (of Electricity) is always valid. This means that the electric flux of E through any closed surface is always proportional to the total enclosed charge within that surface. Applying Gauss' law to the electric field of a point charge (something that we did in this series) we get Coulomb's law. This shows us that Gauss's law is consistent with Coulomb's law.
The integral form finds application in calculating electric fields around charged objects, which is something that we covered in depth! The area integral of the electric field gives a measure of the net charge enclosed. The divergence of the electric field (differential form) gives us a measure of source density and has implications for the conservation of charge.
Sometimes εo is being replaced with 4πk and so the law is at last stated as:

or
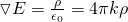
which are two equivalent equations...
Note that I use E instead of D, cause ε0 doesn't occur for the "D-equation".
Equation 2: Gauss' Magnetism Law
The second equation is the magnetic equivalent of Gauss's law of Electricity, which was the first equation. This equation describes that magnetic field-lines form closed loops that neither converge nor diverge and shows us that magnetic monopoles do not exist. Coulomb force acts between the poles of a magnet. Gauss's Magnetism Law states that:
The magnetic flux through any closed surface is equal to zero.
Mathematically this can be written as:
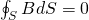
or in the differential form:
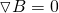
So, for magnetic dipoles (which naturally occur in nature in the form of magnets / magnetic materials or can be "created" by current - electromagnets) the total magnetic flux in any closed surface is zero. The magnetic flux directed inward toward the south pole is therefore equal to the flux outward from the north pole. A theoretical magnetic monopole would give a non-zero area integral. From all this we can again see that Gauss's law works on the principle that no magnetic monopoles exist (something that might change...we will see in the future!).
Equation 3: Faraday's Law
The third equation is Faraday's law and describes how changing magnetic field generate/induce electric fields. Faraday's law states that:
The line integral of the electric field around any closed loop is equal to minus the time rate of change of the magnetic flux through the loop.
Mathematically this can be written as:

where S' is a surface attached to a loop C.
The differential form of Faraday's law of induction is:
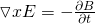
The minus that occurs in these equations can be explained using Lenz's law. The induced current and electric field always tries to oppose the effect caused by electromagnetic induction. That's why the direction of the produced magnetic flux is in the opposite direction of the magnetic flux change. When the magnetic field changes then the electric field lines curl (in other cases they don't). Such electric fields are being produced by the so called Eddy currents.
The line integral is equal to the generated voltage or induced emf in the loop and so Faraday's law is the basis of electric generators, inductors and transformers.
Equation 4: Ampere's Law
The fourth and final equation is Ampere's circuital law, which is a law that describes how electric currents generate magnetic fields. The non-extended law states that:
The line integral of the magnetic field around any closed loop is equal to times the algebraic sum of the currents which pass through the loop.
This can be mathematically as:
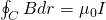
where I is the net current flowing through a loop C.
Using the electrical current density per unit of area j the equation can be written as:
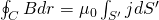
where S' is again a surface attached to a loop C.
As we saw throughout this series, electric current is not the only source of magnetic fields. Magnetic fields can also be produced by the so called displacement current caused by the magnetic flux change and so in absence of conductive current. Maxwell extended Ampere's law including the magnetic field produced by such currents. Magnetic field lines curl around electric current, but also when electric fields change. The extended law is written as:
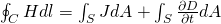
where B is being replaced by H, making the component μ0 "disappear".
In differential form the same law is being written as:
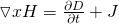
with J being the displacement current density.
To summarize we see that magnetic fields can be generated by electric fields and currents, but also changing fields that cause displacement current.
Using constants Ampere's law can also be written as:
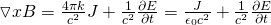
Ampere's law is generally useful when calculating magnetic fields. To apply this law we have to choose a closed Amperian loop, which is free for us to choose and the only dependency is a closed loop.
I tried to put together as much "simple" and useful information as possible to make you understand the equations in principle. Reading this article you of course don't know how to apply them for any electromagnetic case and application, but you should have a great general knowledge. For more information, which includes complex math, you can head to my reference sources that follow now!
REFERENCES:
- https://www.britannica.com/science/Maxwells-equations
- http://www.maxwells-equations.com/
- http://farside.ph.utexas.edu/teaching/302l/lectures/node116.html
- https://simple.wikipedia.org/wiki/Maxwell%27s_equations
- https://physics.info/maxwell/
- http://www.feynmanlectures.caltech.edu/II_18.html
- http://hyperphysics.phy-astr.gsu.edu/hbase/electric/maxeq.html
- http://hyperphysics.phy-astr.gsu.edu/hbase/electric/maxeq2.html#c1
Mathematical equations that I had in this post where drawn using quicklatex!
Previous posts about Electromagnetism
Electric fields:
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
Electric flux:
Electric flux and Gauss's law -> Electric flux, Gauss's law
Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications
Applications of Gauss's law (part 2) -> more Gauss applications
Electric flux exercises -> examples in electric flux and Gauss's law
Electric potential:
Electric potential energy -> explanation of work-energy, electric potential energy
Calculating electric potentials -> more stuff about potential energy, potential, calculating potentials
Equipotential surfaces and potential gradient -> Equipotential surface, potential gradient
Millikan's Oil Drop Experiment -> Millikan's experiment, electronvolt
Cathode ray tubes explained using electric potential -> cathode ray tube explanation
Electric potential exercises (part 1) -> applications of potential
Electric potential exercises (part 2) -> applications of potential gradient, advanced examples
Capacitance:
Capacitors (Condensers) and Capacitance -> Capacitors, capacitance, calculating capacitance
How to solve problems around Capacitors -> combination, solving problems, simple example
Electric field energy and density -> Electric field energy, energy density
Dielectric materials -> Dielectrics, dielectric constant, permittivity and strength, how to solve problems
Electric capacitance exercises -> examples in capacitance, energy density and dielectrics
Current, resistance and EMF:
Electric current -> Electric current, current density
Electrical resistivity and conductivity -> Electrical resistivity, conductivity, thermal coefficient of resistivity, hyperconductivity
Electric resistance -> Resistance, temperature, resistors
Electromotive Force (EMF) and Internal resistance -> Electromotive force, internal resistance
Power and Wattage of Electronic Circuits -> Power in general, power/wattage of electronic circuits
Electric current, resistance and emf exercises -> exampes in all those topics
Direct current (DC) circuits:
Resistor Combinations -> Resistor combinations, how to solve problems
Kirchhoff's laws with applications -> Kirchhoff's laws, how to solve problems, applications
Electrical measuring instruments -> what are they?, types list, getting into some of them, an application
Electronic circuits with resistors and capacitors (R-C) -> R-C Circuit, charging, time constant, discharging, how to apply
RC circuit exercises -> examples in Kirchhoff, charging, discharging capacitor with/without internal resistance
Magnetic field and forces:
Magnetic fields -> Magnetism, Magnetic field
Magnetic field lines and Gauss's law of Magnetism -> magnetic field lines, mono- and dipoles, Flux, Gauss's law of magnetism
The motion of charged particles inside of a magnetic field -> straight-line, spiral and helical particle motion
Applications of charged particle motion -> CERN, Cyclotrons, Synchrotrons, Cavity Magetron, Mass Spectrometry and Magnetic lens
Magnetic force applied on Current-Carrying Conductors -> magnetic force on current-carrying conductors/wires, proofs
Magnetic force and torque applied on current loops (circuits) -> magnetic force on current loops, magnetic moment and torque
Explaining the Physics behind Electromotors -> tesla, history and explaining the physics behind them
Magnetic field exercises -> examples in magnetic force, magnetic flux, particle motion and forces/torque on current-carrying conductors
Magnetic field sources:
Magnetic field of a moving charged particle -> moving charge, magnetic field, force between parallel charged particles
Magnetic field of current-carrying conductors -> magnetic field of current, Biot-Savart law
Force between parallel conductors and the magnetic field of a current loop-> force between parallel conductors, magnetic field of current loop
Ampere's law and Applications -> Ampere's law, applications
Magnetic materials -> Magnetic materials, classification and types, material examples
Displacement current -> Displacement current, Extension of Ampere's law
Exercises in Magnetic field sources -> examples all around magnetic field sources
Electromagnetic Induction:
Electromagnetic Induction and Faraday's law -> Electromagnetic Induction, Experiments, Faraday's law
Motional Electromotive Force (Emf) -> Motional Emf, Faraday's law and motional emf, generalization
Lenz's law and Induced Electric fields -> Lenz's law, Induced Electric Fields
Eddy Currents and Applications -> Εddy currents, applications (brakes, testing, others)
And this is actually it for today's post! I think that this whole article was a great reminder of a lot of what we talked about in Electromagnetism in total until now! Next time in Physics we will get into exercises/examples all around Electromagnetic Induction!
Bye bye!
