
Image source: 
Introduction
Hello it's a me again Drifter Programming! Today we continue with Electromagnetism to get into Magnetic field exercises/examples. We will finally get into actual mathematical applications around magnetic fields, magnetic flux and Gauss's law of Magnetism, the motion of particles inside of a magnetic field and the magnetic force on straight-line conductors and force/torque on current-carrying conductor loops. I will of course split the examples around these exact topic that we talked about! So, without further do, let's get started!
Magnetic fields
In magnetic field on their own we don't have so much to talk about. So, this section will be a small recap in what magnetic fields are and what rules they follow.
Magnetic fields are mainly produced by magnets that come "in pairs of two poles" and act similar to an electric dipole. A magnet is build up of two poles which are called North and South pole. The magnetic field lines emerge from North poles and enter South poles by forming closed loops. The density of those lines indicates the field strength and the direction of the magnetic field is always tangent to the field line. The magnetic field lines (like electric field lines) cannot intersect/cross each other. When more then one magnetic fields are inside of a region then the total magnetic field that affects say a particle inside of the region is equal to the vector sum of all magnetic field strengths at the point where the particle is (superposition principle). We can theoretically artificially construct monopoles that will act like single magnetic "charges", which is not yet done. Breaking a bar magnet in half for example, doesn't split the poles and just construct two new magnets where each one has a North and South pole.
After all this you can quite imagine that a magnetic field looks like this:

Image source: 
(Simple) Magnetic force
The magnetic force is given by:

where:
- F is the magnetic force (in Newton's)
- q the magnitude of charge (in Coulomb)
- v the drifting velocity of the charge (in m/s)
- B the strength of the magnetic field (measured in Tesla)
- φ the angle of the velocity and magnetic field
The direction of the magnetic force is perpendicular to the motion of the particle and goes to a "third" dimension (cross product between vectors). To find the direction we use the so called right hand rule.
Let's get into an actual mathematical application for that!
Example:
Consider a proton that moves into a magnetic field with an angle of φ = 30°. The magnetic field has a strengh of 2T and the velocity of the proton is v = 3x10^5 m/s. Remember that the magnitude of charge of a proton is: |e| = 1.6x10^-19C. Calculate the force applied on the proton (magnitude and direction).
Let's suppose that the magtnetic field is parallel to the z-axis and that the proton moves with an angle to the positive x-axis. From the right hand rule we have that the force is applied in the y-axis and more specifically on the negative y-axis.
The magnitude of the magnetic force is:

The direction of that force is in the negative y-axis.
Note that we could do the calculations using the "vector-language" and so the unit vectors i, j and k. But, I think it's easier to calculate the magnitude and to find the direction some other way (like the right-hand rule here). Vectors seem difficult for a lot of people :)
Magnetic flux and Gauss's law of Magnetism
1.
Suppose a rectangle surface with an area of A = 3cm^2. We put this surface inside of a uniform magnetic field with a magnetic flux of Φ = 0.9mWb and having an angle of 60° to the field lines. Calculate the magnetic field strength (or magnetic flux density).
We will of course use the magnetic flux equation:

The magnetic field strength and angle are of course the same at all the points of the surface which gives us:

2.
Consider the following "object" with 5 surfaces:

A uniform magnetic field goes in the direction +x (positive x-axis) and has a strength B = 0.6T.
Calculate the magnetic flux in the following surfaces:
- abcd
- befc
- aefd
- total surface
(Exercise in the Physics Book of Hugh D. Young)
1.
The total surface of abcd is easy to find cause it's an rectangle and so is:

(note that I convert cm's into meters)
The surface "points" in the +x-direction and so the total flux is:

2.
The surface befc is again easy to find and is:

But this time this surface is perpendicular to the magnetic field, which means that the total flux is zero.

3.
The surface aefd has an area:
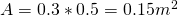
This time the surface vector needs to be splitted into components: one parallel and one perpendicular to the magnetic field. The perpendicular one of course is not affected by the magnetic field and so the only the parallel one "gives" magnetic flux.
In our equation we need the sinus of the angle φ which is:

and so the magnetic flux is:
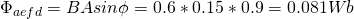
4.
From Gauss's law we know that the total magnetic flux through a closed surface is always zero and so the total magnetic flux through this entire surface is:

I think this example helps you understand how the angle of a surface affects the actual flux that passes through. We had all 4 cases that can occur :)
Motion of particles inside of an magnetic field
1.
Suppose we emit particles with a frequency f = 2450Mhz. Consider those particles being electrons and that we want to make them follow circular paths. Calculate tha magnetic field strengh needed.
Because we are in a circular motion the radial velocity is therefore:
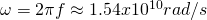
As we know from Mechanics radial velocity and "drifting" velocity are binded by the equation:

and so the magnetic field's strength is:

Note that the mass m and charge q are known constants for the electron!
2.
Consider the following:

An electron has an initial velocity of v =4x10^6m/s and is inside of an uniform magnetic field. The radius of it's circular motion is R = 10cm. It moves from A to B as shown in the diagram.
Calculate:
- The magnitude and direction of the magnetic field
- The time that's needed to move from A to B
(Exercise in the Physics Book of Hugh D. Young)
1.
To make the electron move in a circular path that "goes right" a force in that direction needs to be applied. From the right-hand rule we know that the magnetic field needs to point inwards and so the new and updated diagram is:

The magnetic force is given by:
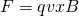
This force also plays the role of the centripedal force, because it causes a circular motion and so:

and of course points inwards...
2.
The trajectrory is of course a semicircle and so the time taken is half the period (T/2) and given by the equation:

Magnetic force and torque on current-carrying conductors
1.
Consider a straight-line conductor with a current I = 50A and a magnetic field of strength B = 1.2T. The conductor is parallel to the x-axis whilst the magnetic field has an angle of 45°. Calculate the magnetic force (magnitude and direction) applied to a section of l = 1m.
Very simple. We just have to use the equation for the magnetic force which gives us:

The direction of that force is of course perpendicular to the planes of the conductor and magnetic field. Considering that the current moves to the right, from the right-hand rule the force points upwards/outwards.
2.
Suppose a circular coil of radius R = 0.05m that is build up of 30 spiral wires. The coil has a current of I = 5A that goes anti-clockwise and is on top of a horizontal plane. The coil is inside of a magnetic field with strength B = 1.2 T that goes from left-to-right. Calculate the magnetic torque applied to the coil by the magnetic field.
The area of the coil is:
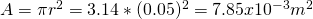
For each spiral the magnetic moment is:

The total magnetic moment is that way:

The magnetic moment and magnetic flux are perpendicular (φ = 90°) cause the magnetic moment is normal to the coil.
The total torque applied to the whole coil is:

REFERENCES:
- The previous articles of the series :D
- The rest is referenced inside of the article
Mathematical equations that I had in this post where drawn using quicklatex!
Previous posts about Electromagnetism
Electric fields:
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
Electric flux:
Electric flux and Gauss's law -> Electric flux, Gauss's law
Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications
Applications of Gauss's law (part 2) -> more Gauss applications
Electric flux exercises -> examples in electric flux and Gauss's law
Electric potential:
Electric potential energy -> explanation of work-energy, electric potential energy
Calculating electric potentials -> more stuff about potential energy, potential, calculating potentials
Equipotential surfaces and potential gradient -> Equipotential surface, potential gradient
Millikan's Oil Drop Experiment -> Millikan's experiment, electronvolt
Cathode ray tubes explained using electric potential -> cathode ray tube explanation
Electric potential exercises (part 1) -> applications of potential
Electric potential exercises (part 2) -> applications of potential gradient, advanced examples
Capacitance:
Capacitors (Condensers) and Capacitance -> Capacitors, capacitance, calculating capacitance
How to solve problems around Capacitors -> combination, solving problems, simple example
Electric field energy and density -> Electric field energy, energy density
Dielectric materials -> Dielectrics, dielectric constant, permittivity and strength, how to solve problems
Electric capacitance exercises -> examples in capacitance, energy density and dielectrics
Current, resistance and EMF:
Electric current -> Electric current, current density
Electrical resistivity and conductivity -> Electrical resistivity, conductivity, thermal coefficient of resistivity, hyperconductivity
Electric resistance -> Resistance, temperature, resistors
Electromotive Force (EMF) and Internal resistance -> Electromotive force, internal resistance
Power and Wattage of Electronic Circuits -> Power in general, power/wattage of electronic circuits
Electric current, resistance and emf exercises -> exampes in all those topics
Direct current (DC) circuits:
Resistor Combinations -> Resistor combinations, how to solve problems
Kirchhoff's laws with applications -> Kirchhoff's laws, how to solve problems, applications
Electrical measuring instruments -> what are they?, types list, getting into some of them, an application
Electronic circuits with resistors and capacitors (R-C) -> R-C Circuit, charging, time constant, discharging, how to apply
RC circuit exercises -> examples in Kirchhoff, charging, discharging capacitor with/without internal resistance
Magnetic field and forces:
Magnetic fields -> Magnetism, Magnetic field
Magnetic field lines and Gauss's law of Magnetism -> magnetic field lines, mono- and dipoles, Flux, Gauss's law of magnetism
The motion of charged particles inside of a magnetic field -> straight-line, spiral and helical particle motion
Applications of charged particle motion -> CERN, Cyclotrons, Synchrotrons, Cavity Magetron, Mass Spectrometry and Magnetic lens
Magnetic force applied on Current-Carrying Conductors -> magnetic force on current-carrying conductors/wires, proofs
Magnetic force and torque applied on current loops (circuits) -> magnetic force on current loops, magnetic moment and torque
Explaining the Physics behind Electromotors -> tesla, history and explaining the physics behind them
And this is actually it for today's post and I hope that you learned something!
Next time we will start getting into Magnetic field sources!
Bye bye!
