Physics - Electromagnetism

Image source: https://commons.wikimedia.org/wiki/File:Lc_circuit.svg

Introduction

Hello it's a me again Drifter Programming! Today we continue with Electromagnetism to get into Inductor-Capacitor (L-C) Circuits. To understand this article better I highly suggest you to go read my articles about Inductors (Inductance, Induction etc.) and Capacitors (Capacitance) first. The previous post about R-L circuits might also become handy...So, without further do, let's get started!

L-C circuit

Electrical circuits that consist of an inductor with inductance L, connected in series with a capacitor of capacitance C are known as LC circuits. In this series and mainly last time we say that inductors are being affected by the so called Self-Induction. This Self-Induction produces an induced emf and current that opposes the change in current that caused it (Lenz's law). That's why a R-L circuit needed some time (5τ) to reach the maximum current/voltage value. The same also applied for the de-energizing (discharging) process, where the inductor worked as a voltage source and opposed the decrease in current caused by the voltage drop in the resistor.

In R-C (resistor-capacitor) circuits we saw that something similar happens with capacitors. Capacitors need some time to get fully charged (5τ with a different τ constant!). When a capacitor is being charged the current that charges it is decreasing, until it reaches a value of zero where the capacitor is fully charged. The same thing also happens when we discharge a capacitor, having the current be at max value and reach a value of zero when completely discharged.

When combining these two components, strange things start happening...

L-C circuit oscillations

Let's consider a L-C circuit that at first is uncharged (no current and no voltage). The inductor and capacitor are connected in serial to a voltage source V at time t = 0. The voltage drop in the capacitor is Q/C, whilst the voltage drop in the inductor is L dI/dt. Applying Kirchhoff's Voltage Law (KVL) we get:

The rate at which charge Q is stored in the capacitor's positive plate is equal to the rate at which current is flowing in the circuit (convervation of energy). After some calculus we end up with:

which is the oscillation frequency of the circuit.

The L-C circuit therefore executes an simple harmonic oscillation of the form:

Where:

I(t) is the current with time
I0 is the maximum current value
ω the oscillation frequency
φ the phase shift

I0 and φ are constants, ω can be calculated easily using L and C, and therefore this equation is an easy way of finding the current at a specific time.

The voltage as a function of time is:

We can clearly see that the voltage oscillates at the same frequency as the current but with a phase shift of π/2 radians. This means that the voltage is max when the current is zero, and vise versa.

The power absorption by the capacitor is P = IxV, which is "simple" to calculate at a specific time using the two previous equations. The total pwoer absorption during a oscillation cycle can be found via integration as:

where T is the oscillation period that ca be found as:

Energy Cases

There are some main energy cases at which an L-C circuit can be found at:

capacitor fully charged - inductor fully de-energized
capacitor completely discharged - inductor fully energized
something in between

Capacitor fully charged

When the capacitor is fully charged all the energy of the circuit is at first stored in the electric field of the capacitor. This energy can be calculated as:

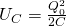
Considering that the capacitor has an initial charge Q0.

After closing the switch / combining it with a inductor at t = 0, the capacitor starts discharging and produces a current in the circuit. That way energy is being transfered from the capacitor to the inductor, causing the electric field to decrease and the magnetic field to increase.

Inductor fully energized

After t = T/4 seconds (and again at 3T/4, but with opposite direction) the inductor now stores all the energy of the field and the current also reaches it's maximum value I0. The energy stored in the inductor, at that exact moment, is:

Having no resistance in the circuit, no circuit is being lost as heat. Therefore these two maximum energy values are equal and so:

In-between cases

At any other time between the capacitor has a charge q(t) and a current i(t) is flowing through the circuit. The total energy in the circuit is therefore a sum of the individual energy "storage" in the inductor and capacitor, giving:

which of course is equal to the maximum value of before, cause no energy is being lost...

Recharge of capacitor

After reaching the maximum current I0 and having all the energy stored in the inductor the capacitor starts recharging. The inductor resists the change in current and so current continues to flow, but now in opposite direction. At this point the electric field is now increasing, while the magnetic field is decreasing, until all the energy is again turned back to the capacitor, making it re-acquire it's maximum charge Q0 (at t = T/2). Of course the capacitor plates now will have an opposite polarity, being charged in the opposite direction.

Re-discharge of capacitor

After the capacitor gets it's maximum charge back, it again starts discharging, re-energizing the inductor until the current becomes max (-I0) where the inductor has been fully energized (t = 3T/4). At this point the inductor then again starts de-energizing in the opposite direction (the initial direction that we had at t = 0) until the capacitor gets charged fully again after a complete oscillation cycle T.

This whole oscillation can be summarized with the following figure:

Image source: https://phys.libretexts.org/.../

At t = 0, T the capacitor has the maximum "positive" charge
At t = T/2 the capacitor has the maximum "negative" charge (inverse polarity)
At t = T/4, 3T/4 the capacitor is fully discharged and inductor fully energized.

Applications

Such circuits (mostly R-L-C, cause there can't be anything without resistance) are mostly used as filters. Other applications include:

Communication systems
Signal processing
Tuning radio TX's and RX's
Voltage magnification
Amplifier circuits
Induction heating
Electronic resonators

Note that this whole articles covered series LC circuits, cause parallel ones have a more complicated behaviour, that we will get back to in alternating current!

REFERENCES:

Mathematical equations that I had in this post where drawn using quicklatex!

Previous posts about Electromagnetism

Electric fields:

Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization

Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples

Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines

Electric dipoles -> Electric dipole, torque, potential and field

Electric charge and field Exercises -> examples in electric charges and fields

Electric flux:

Electric flux and Gauss's law -> Electric flux, Gauss's law

Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications

Applications of Gauss's law (part 2) -> more Gauss applications

Electric flux exercises -> examples in electric flux and Gauss's law

Electric potential:

Electric potential energy -> explanation of work-energy, electric potential energy

Calculating electric potentials -> more stuff about potential energy, potential, calculating potentials

Equipotential surfaces and potential gradient -> Equipotential surface, potential gradient

Millikan's Oil Drop Experiment -> Millikan's experiment, electronvolt

Cathode ray tubes explained using electric potential -> cathode ray tube explanation

Electric potential exercises (part 1) -> applications of potential

Electric potential exercises (part 2) -> applications of potential gradient, advanced examples

Capacitance:

Capacitors (Condensers) and Capacitance -> Capacitors, capacitance, calculating capacitance

How to solve problems around Capacitors -> combination, solving problems, simple example

Electric field energy and density -> Electric field energy, energy density

Dielectric materials -> Dielectrics, dielectric constant, permittivity and strength, how to solve problems

Electric capacitance exercises -> examples in capacitance, energy density and dielectrics

Current, resistance and EMF:

Electric current -> Electric current, current density

Electrical resistivity and conductivity -> Electrical resistivity, conductivity, thermal coefficient of resistivity, hyperconductivity

Electric resistance -> Resistance, temperature, resistors

Electromotive Force (EMF) and Internal resistance -> Electromotive force, internal resistance

Power and Wattage of Electronic Circuits -> Power in general, power/wattage of electronic circuits

Electric current, resistance and emf exercises -> exampes in all those topics

Direct current (DC) circuits:

Resistor Combinations -> Resistor combinations, how to solve problems

Kirchhoff's laws with applications -> Kirchhoff's laws, how to solve problems, applications

Electrical measuring instruments -> what are they?, types list, getting into some of them, an application

Electronic circuits with resistors and capacitors (R-C) -> R-C Circuit, charging, time constant, discharging, how to apply

RC circuit exercises -> examples in Kirchhoff, charging, discharging capacitor with/without internal resistance

Magnetic field and forces:

Magnetic fields -> Magnetism, Magnetic field

Magnetic field lines and Gauss's law of Magnetism -> magnetic field lines, mono- and dipoles, Flux, Gauss's law of magnetism

The motion of charged particles inside of a magnetic field -> straight-line, spiral and helical particle motion

Applications of charged particle motion -> CERN, Cyclotrons, Synchrotrons, Cavity Magetron, Mass Spectrometry and Magnetic lens

Magnetic force applied on Current-Carrying Conductors -> magnetic force on current-carrying conductors/wires, proofs

Magnetic force and torque applied on current loops (circuits) -> magnetic force on current loops, magnetic moment and torque

Explaining the Physics behind Electromotors -> tesla, history and explaining the physics behind them

Magnetic field exercises -> examples in magnetic force, magnetic flux, particle motion and forces/torque on current-carrying conductors

Magnetic field sources:

Magnetic field of a moving charged particle -> moving charge, magnetic field, force between parallel charged particles

Magnetic field of current-carrying conductors -> magnetic field of current, Biot-Savart law

Force between parallel conductors and the magnetic field of a current loop-> force between parallel conductors, magnetic field of current loop

Ampere's law and Applications -> Ampere's law, applications

Magnetic materials -> Magnetic materials, classification and types, material examples

Displacement current -> Displacement current, Extension of Ampere's law

Exercises in Magnetic field sources -> examples all around magnetic field sources

Electromagnetic Induction:

Electromagnetic Induction and Faraday's law -> Electromagnetic Induction, Experiments, Faraday's law

Motional Electromotive Force (Emf) -> Motional Emf, Faraday's law and motional emf, generalization

Lenz's law and Induced Electric fields -> Lenz's law, Induced Electric Fields

Eddy Currents and Applications -> Εddy currents, applications (brakes, testing, others)

Maxwell's equations -> What they are, each equation analyzed separately

Electromagnetic Induction exercises -> examples all around Electromagnetic Induction

Mutual and Self Induction:

Mutual Inductance -> Mutual Inductance, applications

Self Induction -> Self Induction, Lenz's law, Inductance of a Coil

Magnetic Energy Density -> Energy stored in a magnetic field (or inductor), Magnetic energy density, Coaxial Cable Inductance Example

R-L circuits -> R-L circuit energizing, de-energizing, Characteristic time constant

And this is actually it for today's post and I hope that you enjoyed it! Next time in Physics we will get into R-L-C (Resistor-Inductor-Capacitor) Circuits...

Bye bye!

Physics - Electromagnetism - L-C circuits