
Custom Thumbnail that contains:
Introduction
Hello it's a me again Drifter Programming! Today we continue with Electromagnetism to get into Electromagnetic wave exercises. Some of the articles/topics don't need specific applications, which is why I will leave them out from this article, instead of making a complete theoretical rewind like in Alternating current. So, let's get into it!
Sine Waves and Phasors
Let's start out with an example around Sine Waves and Phasors!
Example (Exercise 1.3 of Reference_1):
Consider the following equation for the electric field of an electromagnetic wave:

Determine:
- The direction of wave propagation
- The wave frequency f
- The wavelength λ
- The wave velocity
Solution:
1.
Containing z in the expression the wave of course propagates along the z-axis. For the actual direction that this wave follows on that axis we can check the signs of the coeffiecients of t and z. Both of them are positive and so the wave goes in the -z direction. You could also see that by solving the equation for z and giving incrementing values to t.
2.
The more general expression for waves is:
This shows us that the coefficient of t is equal to ω. By also knowing the relationship of the angular frequency ω to the wave frequency we get:
3.
In the same notion, we can also find the wavelength by looking at the general expression:
We can clearly see that λ is connected with the coefficient of x, which in our case is z. Setting these two equal to each other we get:
4.
The velocity of a wave or phasor is equal to the product of the wavelength and frequency, that we just calculated, and so:

Knowing that EM waves travel in a vacuum (and also approximately in air) at the speed of light which is c = 3 x 10^8 m/s, we can clearly see that the wave propagates through a specific medium that slows it down.
Energy in EM waves
Let's continue with two examples around power/energy density...
Example 1 (Practice Problem 1 From Reference_2)
Consider a 100W light bulb.
Determine the following quantities:
- the peak electric field
- the peak magnetic field
- the radiation pressure
For your calculations suppose that we solve for an imaginary sphere of r = 1m radius that spreads over the surface.
Solution:
1.
We start out with the definition of power density, which is equal to the Poynting vector and given by the mathematical expression:

Knowing that the ratio of Electric to Magnetic field magnitude is equal to the speed of light (c = E/B) we can substitute this into the previus equation to elimiate the electric field, which gives us:

The surface A of the imaginary sphere is:
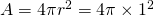
and so solving the equation for E we get:

2.
To calculate the magnetic field we could follow the same procedure by replacing E with Bc or we can simply use the ratio of the two magnitudes which directly gives us:

3.
The radiation pressure is given by the equation:
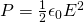
We know all the needed quantities already and so get:

Example 2 (Example 24.4 From Reference_4)
Let's now consider a microwave oven that projects 1kW of microwaves power onto a 30 by 40cm area.
Calculate:
- The intensity I of the radiation (in W/m^2)
- The peak electric field strength E0 in these waves
- The peak magnetic field strength B0
Solution:
1.
The definition for intensity is the power density per unit of area, which is:

The area A can be calculated easily as:
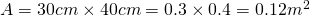
And therefore the (average) intensity is:
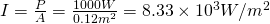
The peak intensity is twice the average and so:
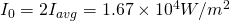
2.
As in the previous example we know that the intensity is equal to the poynting vector, substituting the magnetic field with the elecric field using the ratio, which gives us the following expression for the peak electric field strength:

Entering all the known values we get:
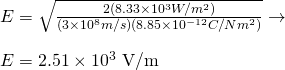
3.
In the same way as in the previous example, the magnetic field strength can be calculated using the relationship of electric and magnetic magnitude, which gives us:
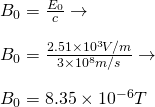
EM Wave Propagation
Let's get into some applications around the propagation of EM waves through matter!
Example 1 (Exercise 7.1 From Reference_1)
Consider a electromagnetic wave of frequency f = 10Mhz, that travels through a non-magnetic medium with μ = μ0 and εr = 9.
Calculate:
- The wave velocity
- the wavenumber
- the wavelength in the medium
- the intrinsic impedance of the medium
Solution:
1.
The velocity of a wave through a medium can we expressed using the electric permittivity ε and magnetic permeability μ of the material as:

where we also had to substitute the speed of light equation that consists of these two constants for vacuum!
Note that the total permittivity is equal to the product of the free space and "material" permittivity.
By entering the known values we get the final velocity of the wave:
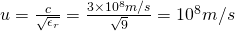
2.
The wavenumber is equal to the ratio of angular to "actual" wave velocity and so:
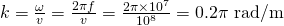
3.
The wavelength can be calculated using the wavenumber as:
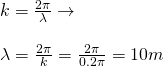
4.
The impedance in the medium is given by the equation:
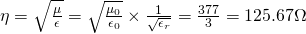
Example 2 (Exercise 7.7 From Reference_1)
Knowing that copper is following the constitutive parameters:
- μ = μ0 = 4π x 10^-7 H/m
- ε = ε0 ~= (1/36π) x 10^-9 F/m
- σ = 5.8 x 10^7 S/m
Assuming that these are frequency independent, in which range of frequencies is copper a good conductor?
Solution:
A good conductor implies that:

Substituting ω we get:
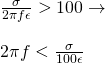
Solving for f we get:

Standing EM waves
I couldn't find any good examples around Standing EM waves and so here comes one by myself.
Example
Consider two reflectors with distance L = 10m.
Calculate:
- the wavelengths and frequencies for which a standing wave can exist
- the nodal and anti-nodal planes of E (or B) for the λ giving with n = 2
Solution:
1.
A standing wave can only be formed when:

From that we have that:

and

2.
The wavelength for n = 2 is:
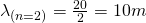
The nodal and anti-nodal planes of E and B are conversly related and so calculating for one gives us the equations for the other one.
The equations for the electric field planes are:

The nodal plane of E is equal to the anti-nodal plane of B, and the anti-nodal plane of E is equal to the nodal plane of B.
Electromagnetic Spectrum
This might be the topic for which I found the most exercises, which sadly are actually similar applications of the equation: "c = λ f". More complicated things get out of the topics that we covered in this series and get into atoms...
Example (Numerical 2 From Reference_3)
Find the range of wavelengths that corresponds to the following frequency ranges:
- AM radio which allocates 530 to 1710Khz
- FM radio which allocates 88 to 108 Mhz
Solution:
1.
Knowing the frequencies we can easily find the wavelengths using the speed of light equation c = λf. Doing so we get:
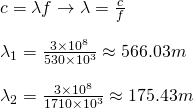
And so the corresponding range of wavelengths is:

2.
In the same notion the wavelengths for FM radio are:
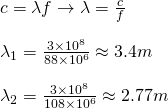
Corresponding to the range:
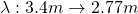
Radiation and Antennas
Lastly let's also get into Antenna exercises, even though we don't got into the most mathematical expressions in the mostly theoretical post about them! But, it's interesting to see all the concepts of Electromagnetic waves to have appliance in antennas.
Example 1 (Exercise 9.1 From Reference_1)
Consider a 1 meter long dipole antenna that is excited by a 5-Mhz current of amplitude I = 5A. What is the power density of the antenna at a distance of 2 km in the broadside direction?
Solution:
First of all we should calculate the wavelength:
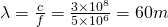
where the frequency of the generated wave is of course equal to the frequency of the actual current/voltage supply.
The power density is given by:

Entering all the known values we get:
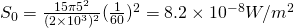
The equation that we used is of course based on the Poynting vector equation, where quantities were substituted, so that we end up only with known quantities.
Example 2 (Exercise 9.6 From Reference_1)
The effective area of an antenna is 9 m^2. Calculate the directivity in dB at 3Ghz.
Solution:
Again, we first have to calculate the wavelength:

The directivity is given by the equation:
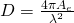
As you can see we already know all the needed quantities. Therefore we get:

Afterwards the exercises start covering things that we don't covered in my theory article!
RESOURCES:
Reference articles:
- http://em.eecs.umich.edu/emag7e/pdf/ulaby_exercise_solutions.pdf
- https://physics.info/em-waves/practice.shtml
- https://physics.info/em-spectrum/problems.shtml
- http://www.wright.edu/~guy.vandegrift/openstaxphysics/chaps/24%20Electromagnetic%20waves.pdf
Mathematical equations that I had in this post where drawn using quicklatex!
Previous articles about Electromagnetic waves
Electromagnetic Wave Introduction -> Electromagnetic waves, velocity, wave equation
Sine waves and EM wave energy -> Sine waves, energy density, EM wave power, Poynting vector, Radiation pressure / Energy momentum
Electromagnetic waves in matter -> Propagation, Angular distribution, polarization and scattering, Interaction with Conductors, Plasma and Dielectrics
Standing Electromagnetic waves -> Standing waves in general, Standing EM waves
Electromagnetic Spectrum -> Electromagnetic Spectrum, Kinds of Radiation/Light, Applications in Astronomy
Antenna Radiation Patterns -> Antennas (theory), Antenna Properties, Radiation Patterns
Final words | Next time
And this is actually it for today's post and I hope that you learned EM waves even better, now that we also got into actual mathematical applications of all that we covered! This is actually the final Electromagnetism stand-alone article that I had in plan. After finishing this series, I'm now thinking of getting into an "All about"-Article that will contain everything that we talked about in the Electromagnetism series (like a recap) and we will of course get back to revive some "older" series and also start new ones :)


Keep on drifting!

