This picture shows exactly what we will get into today :P
Introduction
Hello it's a me again Drifter Programming!
Today we continue with Electromagnetism to get into exercises of potential! More specifically, most exercises will actually be applications of potential on different distributions of charge and because there are a lot of them we will continue on next time!
All the mathematical equation will be drawn using quicklatex!
So, without further do, let's get straight into it!
I will first get into a simple example of electric potential and then get into the applications...
Electric Potential
Suppose we have a proton (charge e =1.6 x 10^-19) that moves in a linear line from point a to b using a linear accelerator, travelling a total distance of d = 0.5m.
The uniform electric field goes in the direction a->b and has a magnitue of E = 1.5 x 10^7 N/C.
Calculate:
a) The force F applied to the proton
b) The work W produced by the electric field
c) The potential difference Va - Vb
Solution:
a)
Because the proton is positively charged the force and electric field are going in the same direction. This means that the Force is:
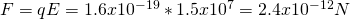
b)
The work is simply the force times the distance and so:

c)
The potential difference can be calculated using the work per charge and so:

Electric Potential Applications
For this "second" part I highly suggest you to read my post about Calculating potential first and mainly the tips!
Charged conducting sphere
Suppose a solid, conductive, charged sphere of radius R with total charge q.
Find the potential at every point inside and outside of the sphere.
Solution:
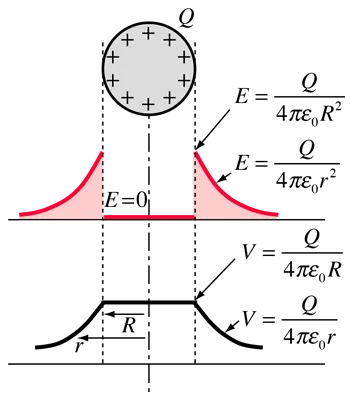
Using Gauss's law in an application of a previous post we ended up with the following:
- For r<R the electric field E is proportional to r
- For r>R we have E being proportional to 1/r^2
With the equations being:

So, when outside of the sphere the field behaves like a point charge q at the center of the sphere.
Which means that if we take V = 0 at infinite distance away we get an equation that gives us the potential at points outside of the sphere with distance r:

The potential exactly at the surface is:

Inside of the sphere the electric field is of course zero (electrostatics). This means that no work is produced whenever we move a test charge between two points inside of the sphere. And so, the potential at every point inside of the sphere is the same that we have at the surface of the sphere.
Here a diagram that shows this:
Arithmetic application?...
Let's say that the potential at a distance r = 0.6m outside of a sphere is 48V.
What is the charge of the sphere if the sphere is supposed very small?
By using the equation outside of the sphere (or the one for point charges) we have:
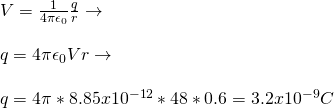
Parallel plates and "another" equation for E
Calculate the potential at any height y between two parallel charged plates (top one positive).
Solution:
The potential energy U from a test charge q' that is a distance y away from the bottom plate is of course:
U = q'Ey
The potential at this point is the potential energy U per charge and so:

The potential is supposed V = 0 exactly on top of the bottom plate where y = 0.
Considering this point being b and the point exactly below the top plate being a we have:

You can see that nothing really changes if there is a potential at the point b.
The potential is of course decreasing linearly to y while going downwards.
At point a, y = d and Vy = Va and so:

This means that the electric field is equal to the quotient of the potential difference by the distance between those plates.
This is of course only true for this kind of "geometry".
Either way, we can now see that the electric field now can also be calculated in V/m where:
1 V/m = 1 N/C
Generally, the volt per meter is more commonly used!
Line of charge (or charged conducting cylinder)
Calculate the potential at a distance r away of a linear distribution of charge with density λ.
Solution:
In a previous post we calculated the electric field of such an surface which is:

which of course is true for linear distributions and cylinders (cause they act like linear distributions and so like if they had the charge concentraded in the center and so in a line).
The potential of any point a to any point b (potential difference) in radial distances ra and rb from the linear distribution is:
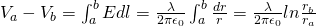
If b is supposed a point with an infinite distance away then Vb = 0 and so:
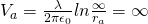
So, by setting V zero at infinity the potential is infinite at any definite distance away of the charge.
To avoid this problem and get a result let's set V = 0 at a point b in a radius r0.
Let's also suppose the radius of a being r.
That way:

For linear distributions any value of r works, but when having a cylinder then this works only for r's that are greater or equal to the radius R of the cylinder.
By selecting r0 = R we get:

which gives us the potential at any point outside of the cylinder (r>R)
Disk of charge
Electric charge is distributed uniformly along a thin disk of radius a and total charge Q.
Calculate the potential at a "axial" distance x away of the center.
(at points that are vertically across to the center and so follow the axis of the center)
Solution:
I already mentioned this in an earlier post:
Electric Field on the Axis of a Uniformly Charged Disk
So, this means that we already know the electric field, let's find out the potential now...
Because the distance r away of the "actual" charge can also be calculated using Pethagora and is:

we can also use this distance that gives us the potential as a function of x and so:

This is the conclusion that we get by using any of the two "methods"
Potential is clearly a scalar unit and so doesn't need components and such things that make our calculations more difficult and so the electric field calculation is not needed, cause we just need the distance.
More specifically when x is much larger then a we can also approximate to:

This of course describes the potential of a point charge Q in a distance x.
So, when being far away from a charged disk the disk acts like a point charge!
Previous posts about Physics
Intro
Physics Introduction -> what is physics?, Models, Measuring
Vector Math and Operations -> Vector mathematics and operations (actually mathematical analysis, but I don't got into that before-hand :P)
Classical Mechanics
Velocity and acceleration in a rectlinear motion -> velocity, accelaration and averages of those
Rectlinear motion with constant accelaration and free falling -> const accelaration motion and free fall
Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
Rectlinear motion exercises -> examples and tasks in rectlinear motion
Position, velocity and acceleration vectors in a plane motion -> position, velocity and accelaration in plane motion
Projectile motion as a plane motion -> missile/bullet motion as a plane motion
Smooth Circular motion -> smooth circular motion theory
Plane motion exercises -> examples and tasks in plane motions
Force and Newton's first law -> force, 1st law
Mass and Newton's second law -> mass, 2nd law
Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
Contact forces and friction -> contact force, friction
Dynamics of Circular motion -> circular motion dynamics, applications
Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
Contact force and friction examples -> exercises in force and friction
Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
Advanced Newton law examples -> advanced (more difficult) exercises
Electromagnetism
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
Electric flux and Gauss's law -> Electric flux, Gauss's law
Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications
Applications of Gauss's law (part 2) -> more Gauss applications
Electric flux exercises -> examples in electric flux and Gauss's law
Electric potential energy -> explanation of work-energy, electric potential energy
Calculating electric potentials -> more stuff about potential energy, potential, calculating potentials
Equipotential surfaces and potential gradient -> Equipotential surface, potential gradient
Millikan's Oil Drop Experiment -> Millikan's experiment, electronvolt
Cathode ray tubes explained using electric potential -> cathode ray tube explanation
And this is actually it for today!
Next time we will get into more examples/exercises of Electric potential!
Bye!
