
Image source: 
Introduction
Hello it's a me again Drifter Programming! Today we continue with Electromagnetism to get into Displacement current. I highly suggest you to go and read my post about Ampere's law first! So, without further do, let's get straight into it!
Ampere's law Refreshment
Ampere's is defined as the following equation:
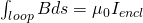
Which means that "the line integral of the magnetic field around an arbitrarily chosen path (the so called Amperian Loop) is proportional to the net electric current enclosed by the path". We calculate a line, closed loop integral of the magnetic field B inside of which a total current Iencl is enclosed. To use this equation you can use any closed path that you want but it's very important that this path is closed! Amperian loops need to be orientated and for that we use the so called right hand "curl" rule. In my previous post we also got into Applications of this law for specific cases, which I would suggest you to check out :)
The first equation is the "simple" form of the equation that applies to magnetic fields of enclosed currents. The extended version contains the concept of displacement current and can be applied for fields where there is no current. To do all this you have to get into the Displacement current...so let's get into it!
Displacement current
So, what is displacement current? In Electromagnetism this phenomenon is analogous to ordinary electric current and is produced by changing electric fields. The current that we covered till now was conduction current and was steady (and will later on also be varying), which means that it was binded to conductors of electricity. This current produced an accompanying magnetic field. Maxwell predicted that a magnetic field must also be associated to changing electric fields even in an absence of conduction current, which was later on verified experimentally. Magnetic fields are associated with currents and so this "new form" of producing magnetic fields was called displacement current. Displacement current is proportional to the rate of change of the electric field. So, as we can see magnetic fields can be produced by moving charges (conventional conduction current) or varying/changing electric fields (displacement current). To distinguish them we write the first current as ic (conduction) and the "new" form as id (displacement).
As you might remember from electric currents those currents had a current density J. Displacement current also has a density which is defined as:

where:
- J is the current density
- ε0 the permittivity of free space
- E the electric field (the change by time)
The density is calculted in A/m^2 (amps per square meter)
A way of defining displacement current is using electric flux as following:

where:
- I is the displacement current
- ε the permittivity (ε = ε0*εr | electric constant * relative permittivity of dielectric)
- Φ the electric flux (the change of it by time)
Capacitor
A great example with which you can understand the concept better are the capacitors. There is no (ordinary) conduction current as electric charges flow through the insulation from one plate to the other. But magnetic effects are still present, which means that displacement current "flows" through this area. The magnitude of the displacement current calculated is equal to the conduction current when charging or discharging the capacitor.
Displacement current generally plays a central role in the propagation of electromagnetic radiation (like light and radio waves) and also gave Maxwell insight of understanding the propagation of electromagnetic waves (that we will talk about later on in this series) that are completely detached from electric crurents of conductors!
Extension/Fix of Ampere's law
Let's extend Ampere's law now to also contain magnetic fields that are produced by displacement current! To do this let's first replace the enclosed current in Ampere's law with a current density integral likes that:
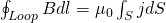
where the right side now contains the integral of j*dS (current density in a infinitesimal surface dS) which is a surface integral along the total surface S where the current is being enclosed. This surface can be any surface bounded by the closed Amperian loop. But, for some surfaces the current is still zero which causes an inconsistency. After a long proof where we are using the flux or electric field change by time, we end up with the final equation:
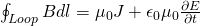
where:
- B is the magnetic field (integral along a Amperian loop)
- ε0 and μ0 the same constants as before
- J the current density
- E the electric field (change by time)
Application for a parallel plate capacitor
The displacement current can be found by solving:

For parallel plate capacitor we know that E = V/d from where:
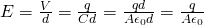
The change of the electric field therefore now is:
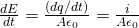
By replacing this component in the first equation we get that id = ic and so the displacement current is equal to the conduction current bringing charge to the plates, exactly as we said previously.
REFERENCES:
- https://www.britannica.com/science/displacement-current
- http://farside.ph.utexas.edu/teaching/em/lectures/node46.html
- http://www.physics.louisville.edu/cldavis/phys299/notes/mag_displacement.html
- http://scienceworld.wolfram.com/physics/DisplacementCurrent.html
- https://www.quora.com/What-is-displacement-current
Mathematical equations that I had in this post where drawn using quicklatex!
Previous posts about Electromagnetism
Electric fields:
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
Electric flux:
Electric flux and Gauss's law -> Electric flux, Gauss's law
Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications
Applications of Gauss's law (part 2) -> more Gauss applications
Electric flux exercises -> examples in electric flux and Gauss's law
Electric potential:
Electric potential energy -> explanation of work-energy, electric potential energy
Calculating electric potentials -> more stuff about potential energy, potential, calculating potentials
Equipotential surfaces and potential gradient -> Equipotential surface, potential gradient
Millikan's Oil Drop Experiment -> Millikan's experiment, electronvolt
Cathode ray tubes explained using electric potential -> cathode ray tube explanation
Electric potential exercises (part 1) -> applications of potential
Electric potential exercises (part 2) -> applications of potential gradient, advanced examples
Capacitance:
Capacitors (Condensers) and Capacitance -> Capacitors, capacitance, calculating capacitance
How to solve problems around Capacitors -> combination, solving problems, simple example
Electric field energy and density -> Electric field energy, energy density
Dielectric materials -> Dielectrics, dielectric constant, permittivity and strength, how to solve problems
Electric capacitance exercises -> examples in capacitance, energy density and dielectrics
Current, resistance and EMF:
Electric current -> Electric current, current density
Electrical resistivity and conductivity -> Electrical resistivity, conductivity, thermal coefficient of resistivity, hyperconductivity
Electric resistance -> Resistance, temperature, resistors
Electromotive Force (EMF) and Internal resistance -> Electromotive force, internal resistance
Power and Wattage of Electronic Circuits -> Power in general, power/wattage of electronic circuits
Electric current, resistance and emf exercises -> exampes in all those topics
Direct current (DC) circuits:
Resistor Combinations -> Resistor combinations, how to solve problems
Kirchhoff's laws with applications -> Kirchhoff's laws, how to solve problems, applications
Electrical measuring instruments -> what are they?, types list, getting into some of them, an application
Electronic circuits with resistors and capacitors (R-C) -> R-C Circuit, charging, time constant, discharging, how to apply
RC circuit exercises -> examples in Kirchhoff, charging, discharging capacitor with/without internal resistance
Magnetic field and forces:
Magnetic fields -> Magnetism, Magnetic field
Magnetic field lines and Gauss's law of Magnetism -> magnetic field lines, mono- and dipoles, Flux, Gauss's law of magnetism
The motion of charged particles inside of a magnetic field -> straight-line, spiral and helical particle motion
Applications of charged particle motion -> CERN, Cyclotrons, Synchrotrons, Cavity Magetron, Mass Spectrometry and Magnetic lens
Magnetic force applied on Current-Carrying Conductors -> magnetic force on current-carrying conductors/wires, proofs
Magnetic force and torque applied on current loops (circuits) -> magnetic force on current loops, magnetic moment and torque
Explaining the Physics behind Electromotors -> tesla, history and explaining the physics behind them
Magnetic field exercises -> examples in magnetic force, magnetic flux, particle motion and forces/torque on current-carrying conductors
Magnetic field sources:
Magnetic field of a moving charged particle -> moving charge, magnetic field, force between parallel charged particles
Magnetic field of current-carrying conductors -> magnetic field of current, Biot-Savart law
Force between parallel conductors and the magnetic field of a current loop -> force between parallel conductors, magnetic field of current loop
Ampere's law and Applications -> Ampere's law, applications
Magnetic materials -> Magnetic materials, classification and types, material examples
And this is actually it for today's post! Next time we will get into the promised exercises/applications all around the topic of Magnetic field sources!
Bye!
