
Hello it's me again! Today we get into the first promised examples for the Newton law applications! I will cover object equilibrium (1st law) and some 2nd law applications! I would suggest you to read some of my previous posts first and then get into these examples, so that you understand them better (if you don't know about the laws already)!
Suggested posts:
So, without further do, let's get into it now!
Object Equilibrium:
Example 1:

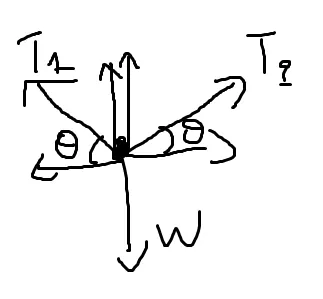
Someone crazy crosses two mountains that are connected with a rope, using that rope, where at the bottom there is a cliff. Supposing that the break tension of the rope is 24,000 N, the person has a mass of 90 kg and that he is at the center of the mountains find the following:
a) if the angle at each side is θ=15 degrees calculate the rope's tension (T)
b) find the least angle θ so that the rope doesn't break
gravity g is 10 m/s^2
a)
Cause the person is at rest we use Newton's first law!
Each half of the rope exerts a force on him with a angle θ to the weight.
The free-body diagram looks like this:
 (digitizer drawing)
(digitizer drawing)
The horizontal component are equal (T2cosθ == Τ1cosθ) and so T1 = T2 = T!
Applying Newton's 1st law vertically we have:
T1sinθ + T2sinθ - mg = 0 =>
2Tsinθ = mg =>
T = mg / 2sinθ =>
T = 90 * 10 / 2 * 0.25 =>
T ~= 1800 N for each side
b)
Using the same relation as before (2Tsinθ = mg) but setting T = 24,000N we now find θ:
sinθ = mg/2T = 90*10 / 2*24,000 =>
sinθ = 0.01 => θ ~= 0.57 degrees
which is the minimum degree.
Example 2:
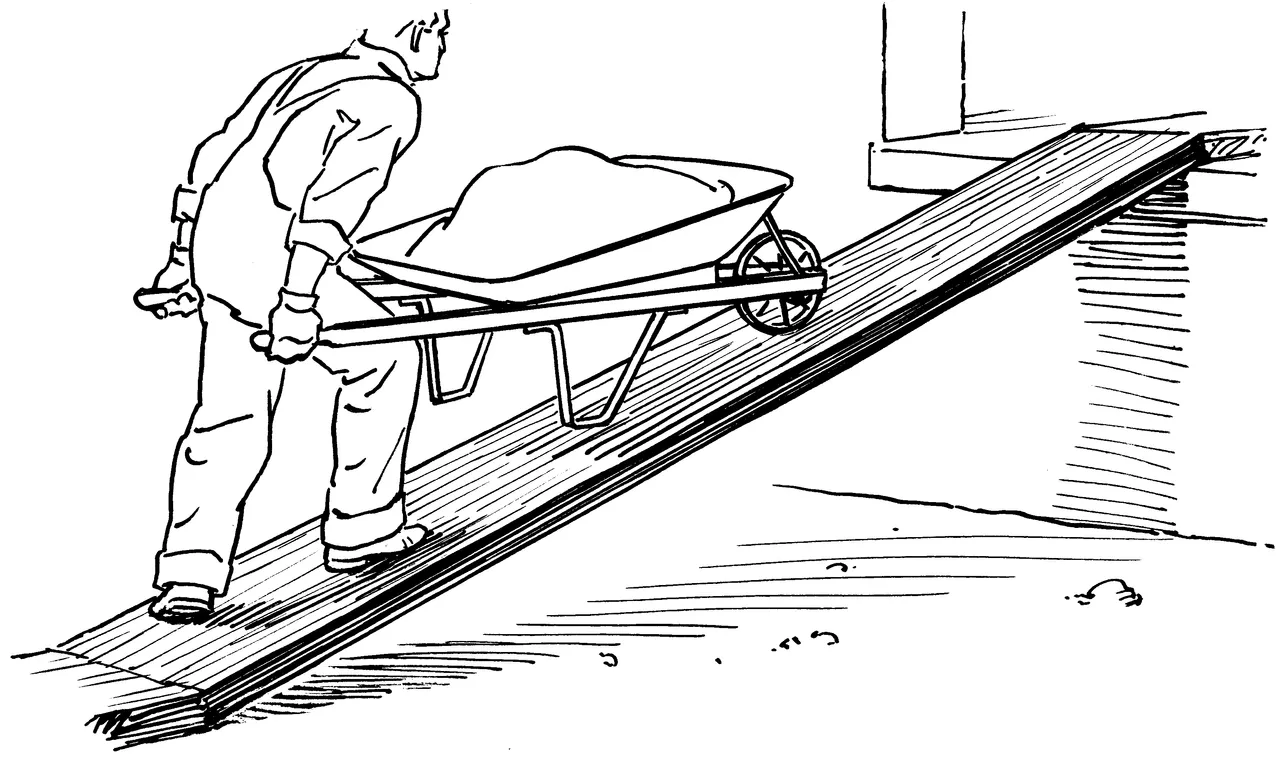
A man pushes an object with 140kg mass with an constant velocity on top of a inclined plane with 37 degrees. If there is no friction and the force applied of the man is parallel to the inclined plane calculate the meter of that force.
We analyze the weight and get:
 (digitizer drawing)
(digitizer drawing)
Because the velocity is constant Newton's 1st law applies and so we have the following for the "horizontal" axis:
F = mgsinθ =>
F = 140*10*sin(37) =>
F = 840N
2nd law applications:
Example 1:
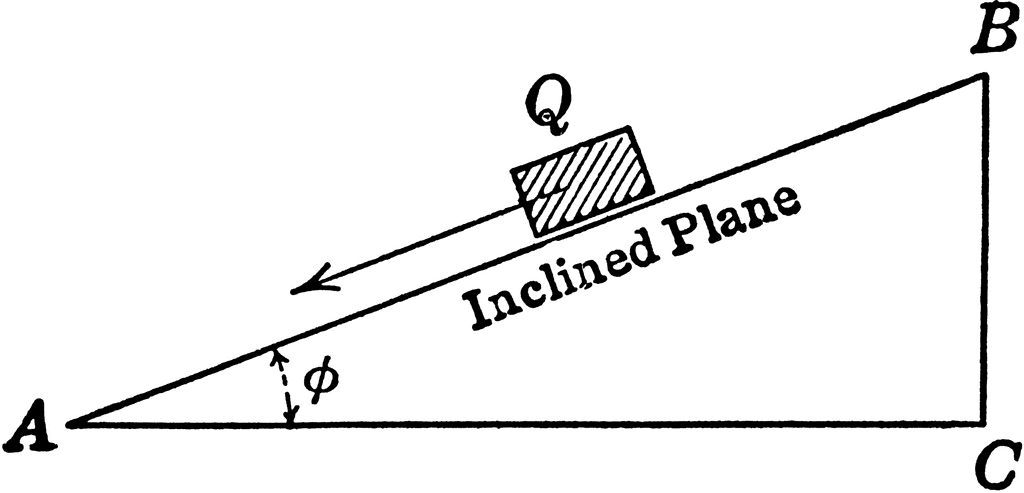
A cube is being pout (first at rest) to the highest point of a inclined plane of 4m distance. It then starts going down and reaches the base in 2 seconds. Let's calculate the inclined plane angle (θ).
The only force applied to the object is the gravity and this force is constant (we suppose that the weight doesn't change).
Analyzing the weight like before we find out that mg*sinθ is the force applied for the object's motion.
Using Newton's 2nd law we have:
F = ma => mg*sinθ = ma => 10*sinθ = a (I)
The force is constant and so the object has a rectlinear motion with constant acceleration and using the distance and time we can calculate the acceleration!
x = x0 + u0t + 1/2 at^2 =>
0 = 4 + 0 + 1/2*a*2^2 =>
a = -4/2 =>
a = -2m/s^2 (II) and we are going downwards
Because of I and II we have:
sinθ = -2/10 = -0.2 =>
θ = arctan(-0.2) => θ ~= 11.3 degrees
Example 2:
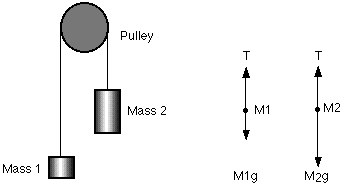
We have a Atwood machine, where in one side we have 15kg(m1) and at the other 30kg(m2) masses. We suppose that the pulley has no friction and so the thread has no resistance. The biggest mass is "higher" and the system is first at rest and then get's set free.
Calculate:
a) the acceleration (upward) of the "smaller" mass
b) the thread's tension (T)
a)
The weight of each object is:
W1 = 15*10 = 150N and W2 = 30*10 = 300N
For the 1st object we have:
T - m1g = m2a (cause the tension is bigger then the weight)
For the 2nd object we have:
m2g - T = m1a (cause the tension is less then the weight)
By adding we get the acceleration:
a = g(m2 - m1)/(m1+m2) =>
a = 10 * (30 - 15)/(30+15) =>
a ~= 3.33 m/s^2
b)
For the thread's tension we use the same equation by substituting with one of the 2nd law equations.
That way using m2g - T = m1a we get:
T = 2g*m1*m2 / m1+m2 =>
T = 200N
Image Sources:





And this is actually it! I hope you learned a lot!
Next time we will get into examples for friction and contact forces!
Bye!
