Hello it's a me again drifter1! Exams are finally over and the last week of them was dramatic and so I didn't find any time to post, but here I am again to post about Physics! Today we will get into how we apply each of the laws and when each of them is useful.
You can find the posts about each law in my blog.
Newton's Laws:
Newton's 3rd law and mass vs weight
Free-body diagram
To start the application we first have to draw a free-body diagram. This diagram contains all the forces that are applied to an object like gravity or friction.
To make it follow these rules/steps:
- Choose and define the right coordination system. You have to show the center of the axes and each axis with it's corresponding direction. For example we tend to set the positive direction as the direction of the acceleration (even if it's "negative" sometimes)
- Be consistent with your signs. Acceleration, velocity and (components of) forces that are pointing towards the positive direction you defined are also positive!
- Draw the forces that are applied TO that object and not FROM that object to others.
- You don't have to be a professional drawer. When dealing with "2d" physics think of the object as an point of mass, that is not wrong because we are applying the laws by supposing exactly that. Also, try using different colors for each force, velocity, acceleration to distinguish them better.
- Determine the known and unknown forces, velocities, accelerations etc. If you don't know the direction then draw it supposing it's positive or negative, knowing that the final algebraic value (meter) might be either positive or negative. When it's positive then you where right, else the actual force is being applied in the opposite direction you drawn.
- Always check the measurement so that you use the same metrics for stuff of the "same" type. We tend to use the S.I. System for the metrics.
An example:
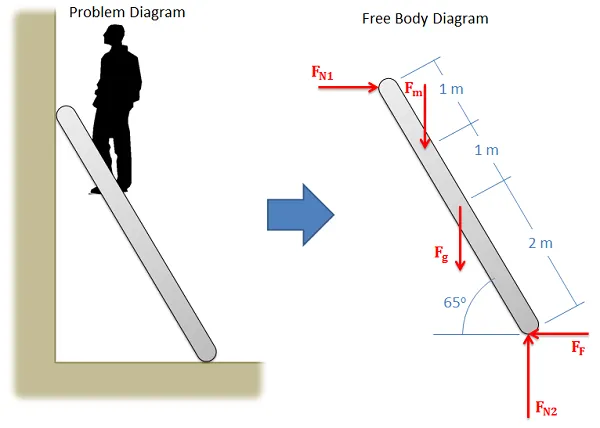
Physics Classroom has some great examples here.
Point equilibrium
When an object is at rest and so in a point equilibrium the total force ΣF applied to it is 0. This means that we use the 1st law.
I an equilibrium we set ΣF = 0 which can also be applied to each axis:
ΣFx = 0
ΣFz = 0
...
This means that we first draw the free-body diagram of that "resting object" and then the total algebraic and vectorial addition of the forces in each axis will be zero.
The 1-dimensional equilibriums are easy to be applied.
The inclined plane (ramp) and 2-dimensional equilibriums in general are more interesting.
To solve them we mostly have to use component vectors so that it's easier to be applied on each axis.
Example
In the following diagram you can see an object on top of an inclined plane where:
- the ramp has a degree θ
- an force f is applied to push the object upwards
- gravity pushed the object down and can be analyzed to 2 components
- the ground/ramp pushed the object up
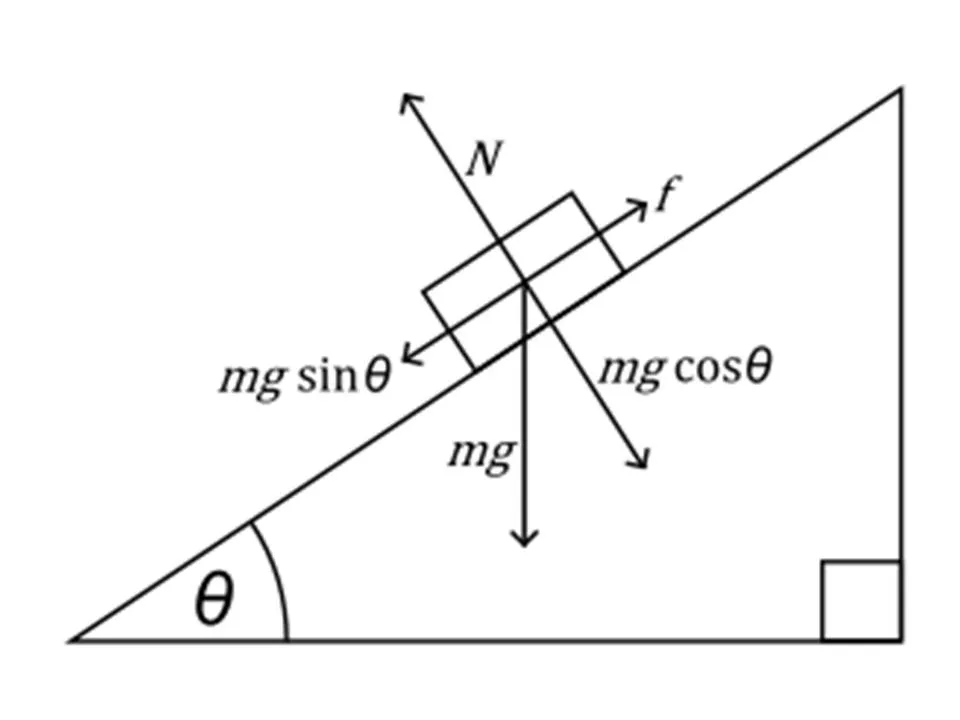
So, to apply the equilibrium we set:
N = mgcosθ and f = mgsinθ
You can see that the coordination system is also in an degree.
That way we apply the law easier.
We can also apply it on threads with friction something that we will discuss next time.
2nd law applications
When the total force ΣF is not 0 then ΣF = ma and we use the 2nd law.
We again mostly use it on each axis independently:
ΣFx = m*ax and ΣFy = m*ay
We again draw the free-body diagram and determine the moving objects.
After that you can apply the law for the motion axis and mostly in one of the axes there will be an equilibrium again that will help you calculating other stuff.
Examples:
- A force F is applied to the object and gravity is vertical to it's motion and so ΣFx = F = ma. On the y or "gravity" axis we will have an equlibrium from where we can calculate the force of the ground that equals gravity.
- The friction T of an Elevator where ΣFy = W - T = mg - T = m*ay.
- Acceleration on top of an inclined plane (ramp) with degree θ, where we have to find the component vectors and then ΣFx = mgsinθ = m*ax. The ground force will be N = mgcosθ.
- An accelerometer that combines both the friction T of an thread and the gravity.
What about the 3rd law?
Well the 3rd law is used everytime, cause it's about action-reaction!
We use it when drawing the free-body diagram for example.
This means that it's more useful and meaningful in stuff that contains friction and contact forces for example. That's exactly the topic of my next post!
Image Sources:


And this is actually it! I hope you enjoyed it!
Next time we will get into Contact forces and friction!
Bye!
