
School has started up again, and just yesterday I had the opportunity to teach one of my favorite topics in Calculus -- L'Hopitals Rule for calculating indeterminate limits.
In 1696 Guillaume de l'Hôpital published Analysis of the Infinitely Small for the Understanding of Curved Lines, or Analyse for short. In this work, L'Hôpital laid out a really ingenious method for calculating limits of indeterminate form, a big pain point when trying to use direct substitution to calculate limits. More on this later.
For now, let's dive into the rule that essentially made l'Hôpital a total rock star.
It goes like this. A limit is a value that a function approaches equally from both sides. Typically to calculate a limit, one might use direct substitution as a fairly quick method. Take, for instance, the following example:

Since the curve f(x) = x^2approaches 4 on both sides of x = 2, we say the limiting value is 4. In order for a limit to work, the approach from both sides must be equal.
To my students, I always say finding a limit is like popping a pimple -- if you don't squeeze it the same way from both sides, it won't pop!

Some functions aren't as simple though
Take the curious example below of calculating the limit of f(x) = sin(x)/x as x approaches 0.
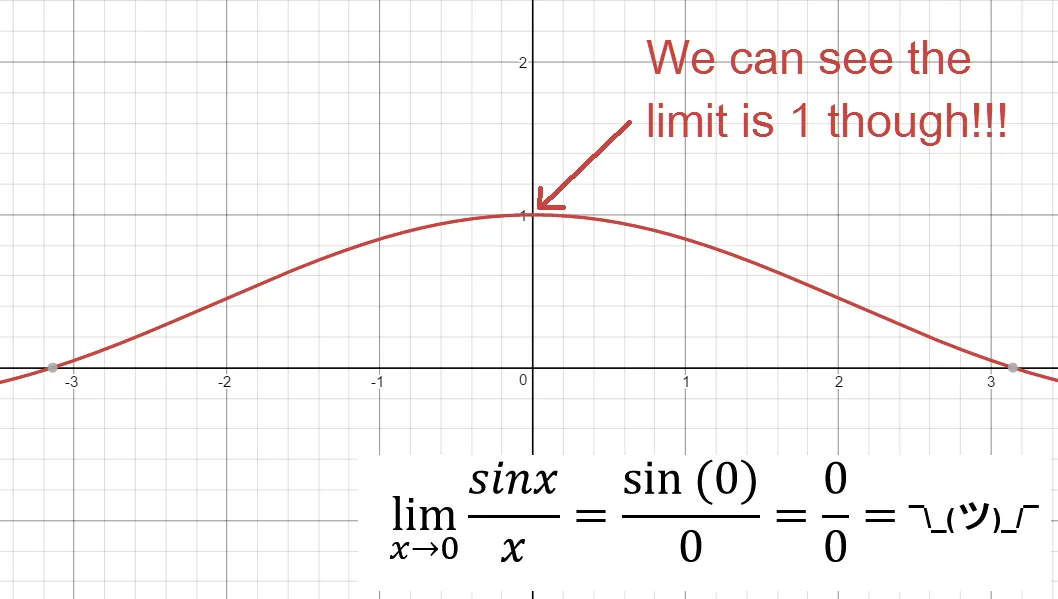
Clearly there is a limit from the graph, but direct substitution yields what is called an indeterminate form. Indeterminate just means exactly that - it is a form of an expression that is not definitively or precisely determined. Usually when 0 is in the numerator of a fraction, we get 0 as a result. But, when 0 is in the denominator, we get undefined as a result.
So what gives when 0 is both on top and bottom? Just rely on the graph? Thinking like a 17th century mathematican, that would be absurd. Graphing calculators didn't exactly exist back in the day.
There is a much better way. And that is how we arrive at L'Hopital's Rule.

TL;DR - When you are evaluating a limit that is indeterminate, you just need to re-express the numerator and denominator functions in terms of their derivative functions. Then, re-evaluate your limit by direct substitution.
This works because of the locally linear relationship a derivative f'(x) has with f(x). A derivative is essentially a tangent line to a curve at a point. If you observe the following, there is literally no difference between finding the limit of a curve f(x) and its derivative function f'(x) at the point of tangency.

Back to our indeterminate example:
Let's now apply L'Hôpital's Rule to our indeterminate f(x) = sin(x)/x:
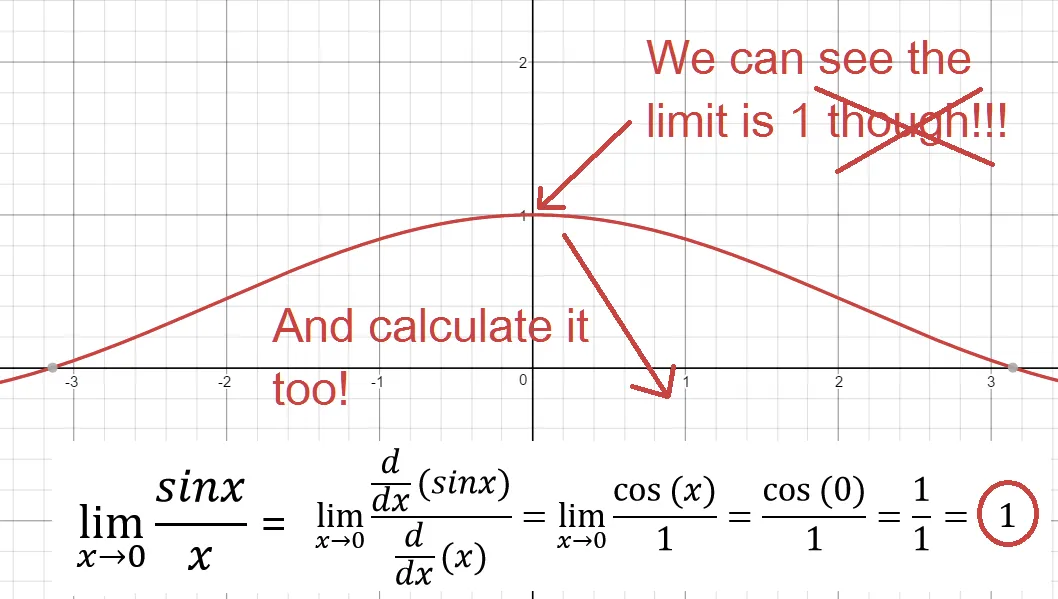
BRILLIANT!
L'Hôpital's Rule is a warm blanket on a cool fall evening. It just works, and when applied properly, make you feel all warm and fuzzy inside. So, you would think for something like this we celebrate l'Hôpital for the absolute genius he was. One problem though:
He probably paid someone for this content.

Johann Bernoulli
The work of l'Hôpital was very well received. Well, by every other mathematician in the world besides Johann Bernoulli, that is. Bernoulli, known as the "Archimedes of his age", was not so keen on l'Hôpital's thoughts, and indicated so in many letters to his closest friends and confidants (one of which so happens to be my Steemit name sake, Leibniz).
In these letters, Bernoulli reveals a different story. That as a younger man, he served as l'Hôpital's personal tutor for a six month time period. In these lessons, according to Bernoulli, he shared his thoughts and theorems on the curvature of curves, local linearity and principles that shaped modern calculus as we know it. One of which, was what we now know as L'Hôpital's Rule.
Friends and other mathematicians wrote off Bernoulli as sour. He was said to be a pretty gruff guy, and he wasn't exactly winning many popularity contests in his day. On his own accord, l'Hôpital was a pretty brilliant mathematician, so these accusations were pretty much written off as slanderous.
It wasn't until he published his autobiography though, shortly before his death, that Bernoulli ultimately "dropped the mic" on l'Hôpital.
Check out this letter, written to Bernoulli from l'Hôpital in 1694, just two short years before l'Hôpital publishes Analyse :
"I will be happy to give you a retainer of 300 pounds, beginning with the first of January of this year ... I promise shortly to increase this retainer, which I know is very modest, as soon as my affairs are somewhat straightened out ... I am not so unreasonable as to demand in return all of your time, but I will ask you to give me at intervals some hours of your time to work on what I request and also to communicate to me your discoveries, at the same time asking you not to disclose any of them to others. I ask you even not to send here to Mr. Varignon or to others any copies of the writings you have left with me; if they are published, I will not be at all pleased. Answer me regarding all this ..." (source)

Bernoulii's response is lost to this letter, but his own proof was published. To understand why Bernoulli would even consider giving up his work, you have to understand the dynamics of the time. Take this, according to Harvard:
While nowadays the difference in social positions seems a trifle, in 1691 it was surely enough to impress even the ebullient self-confidence of John Bernoulli when, freed of worldly cares, he was accepted as an equal and intimate friend in the elegant establishment whose presiding deity [l'Hôpital] was a charming and witty Marquise. (source)
Bernoulli was a modern day Fiverr!
If you think about it, this is a pretty true analogy and fairly relevant to Steemit.
Brilliant guy? ✔️
Marketplace and society that values his thoughts? ✔️
Giving them away for way less than market value? ✔️
If you read about some accusations of stealing content online these days, I suppose history does indeed repeat itself.
I absolutely love teaching this story to my students. It shows there is much more to mathematics besides its natural elegance and beauty from afar. If you step close enough, the brush strokes often reveal more than the sum of those parts together.
