Introduction
Hello it's a me again drifter1!
Last time I said that we would get into Double Integrals, but I forgot one more important thing that we will discuss today!
Today's topic of Mathematics are Total Differentials and how to check if an function f with this df exists.
There is not much more to say so let's get started!
Linear approximation of a function
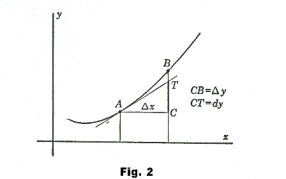
Suppose z = f(x, y) is a plane/surface and P0(x0, y0, z0) the point where the plane z and it's tangent plane cross each other.
We say that:
z = z0 + ∂f/∂x(P0) (x - x0) + ∂f/∂y (P0) (y - y0) = T(x, y)
where z0 = f(x0, y0).
In close points P(x, y) of P0(x0, y0) we have that: f(x, y) ~= T(x, y)
And so:
T(x, y) ~= f(x, y) = f(x0, y0) + fx(P0) (x - x0) + fy(P0) (y - y0)
is called the linear approximation of f(x, y) at P0.
Total differential
This last thing takes us to something else.
Suppose that we now have f(x, y) = 0 as a plane and P0 (x0, y0).
We said that the derivative along a curve is:
df/dt = ∂f/∂x * dx/dt + ∂f/∂y * dy/dt
This can also be re-written like that:
df/dt = fx(P0) * dx/dt + fy(P0) * dy/dt
If we now multiply with dt we get:
df= fx(P0) * dx + fy(P0) * dy
which is called the total differential of f at P0.
So, the derivative of a function f along a curve can then also be represented by a total differential.
But, can we also go in the other way?
For example:
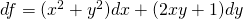
We want to check if an f(x, y) exists so that:
df = fx(P0)dx + fy(P0)dy
This means that:
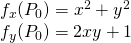
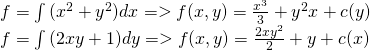
Let's use the 2nd and 3rd equations to find c(y):
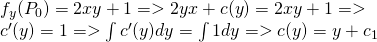
So, then from the 3rd we have:
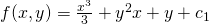
We used this logic in Exact Differential equations, if you remember...
But, yes this worked this time, but will this work everytime?
Checking if f exists with given df
If df = M(x, y)dx + N(x, y)dy = fxdx + fydx then we have:
fx = ∂f/∂x = M
and
fy = ∂f/∂y = N
A rule exists that says that the order of partial differentiation doesn't matter and so:
∂^2f/∂x∂y = ∂^2f/∂y∂x
This means that we can partially differentiate M and N:
∂^2f /∂y∂x = ∂M/∂y = My
∂^2f/∂x∂y = ∂N/∂x = Nx
My = Nx => ∂M/∂y = ∂N/∂x
So, a functions exists, when the condition My = Nx is true!
THIS is true for two variables!!!
By doing the same we can also find the conditions for 3 variables or more.
For 3 variables we have:
df = Mdx + Ndy + Pdz =>
My = Nx, Nz = Py and Mz = Px.
For example:
Let's check this condition for our previous example...

which means that:
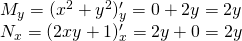
And so:
My = 2y = Nx
which means that a function f exists with this total differential df.
And this is actually it for today and I hope that you enjoyed it!
Next time we will really get into Double integrals :P
Bye!
