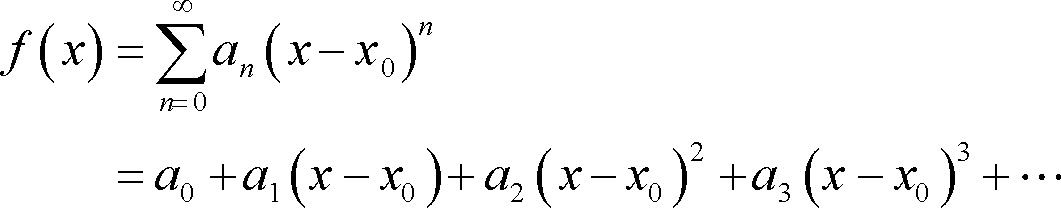
Hello its a me again drifter1! Today we continue with Mathematical Analysis getting into Power Series. I will talk about some of the basics and will leave out the more special ones (Mclaurin and Taylor) for the next post. I suggest you check out my older post about Series Basics first. So, without further do let's get started!
Getting into Function Series:
The Series we covered till now are build up of sequences and represent the limit to infinity of the sum of those sequence-blocks. Using the idea of the power series that we will talk about today, we can then convert any function into a series to get a approximately value for any variable x. This is exactly what we will cover next time and should give you an idea of how useful they are! So, let's get into what Power Series are, how they are build up, convergence etc.
Power Series:
The sequence (Sn(x)) with generic term:
Sn(x) = a0 + a1*(x-x0) + a2*(x-x0)^2 + ... + an*(x-x0)^n for any n in {0, 1, 2, ...},
with ai (i in {0, 1, 2, ..., n}) and x0 being real numbers and x a real variable, is called a powerseries with center x0 and is written like that:
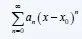
The polynomial Sn(x) for some specific n value is called the partial sum of this series and the functions: a0, a1*(x-x0), a2*(x-x0)^n, ..., an*(x-x0)^n are the terms of the powerseries.
Convergence/Divergence:
Suppose x1 is a real number and the power series x being swapped with x1:
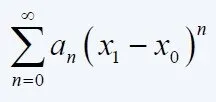
If this series converges (or diverges) then the power series:

also does so, and we say that the powerseries converges (or diverges) at x1.
Example:
Suppose this series:
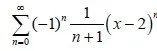
For x = 2 we get a alternating series with (an) = 1/n+1:
- being strictly decreasing and positive for any n
- the limit of (an) giving us 0 when going to infinity and so being a nullsequence
This means that the Leibniz Criterion applies and so the series converges.
Because, this Series converges for x=2 we say that the given powerseries converges at x=2.
Convergence Area:
Convergence/Divergence in Powerseries has to do with the value of x. This means that the Powerseries converges for some specific values of x. So, we specify the Convergence Area of a powerseries as the set of all x in R for which the Series converges.
Suppose the set {r: r = |x - x0|, x in R AND Series converges}.
The number R equals
- 0 when S = {0}
- +∞ when S in not upper bounded
- supS when S!={0} and S is upper bounded
and is called the Convergence Radius of a Power Series.
The range {x0 - R, x0 + R} is called the Convergence Range.
If A is the Convergence Area of a Power series then we can define a function f(x): A -> R, equal to the sum of this powerseries like that:
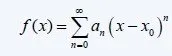
Example:
Suppose the same powerseries as before:

Let's find the Convergence Area, Radius and Range.
In our example previously we already prove that the series converges for x = 2.
Using the Root Test we can prove that the powerseries converges for any x in (1, 3] something that I will leave out, cause it takes some time.
So, |x-2| < 1 and the set:
{r: r = |x - 2|<1, x in R AND Series converges} is upper bounded with supS = 1.
This means that the convergence Radius is R = 1 and we can also specify the Range as:
(2-R, 2+R) = (2 - 1, 2 + 1) = (1, 3).
Because, R is in the range (0, +∞) we also have to check the convergence at the side 1 and 3.
Doing so (something that I will leave out again) you will see that for x = 1 the series diverges and for x = 3 the series converges and so the range is (1, 3].
Convergence Criteria:
To check the convergence we can use 2 similar criteria to the ones we used in "normal" series. The first one being similar to the ratio test and the second one to the root test.
So, with S(an) being a powerseries and R the convergence Radius we have that:
Ratio Test:
R =
- +∞, when lim n->+∞ |an+1/ an| = 0
- 0, when lim n->+∞ |an+1/ an| = +∞
- 1 / lim n->+∞ |an+1/ an|, when lim n->+∞ |an+1/an| = l in R
For R = +∞ the series converges for any real x.
For R = 0 the series diverges for any x in R except x0.
For the last one the Convergence Range is (x0 - R, x0 + R)
Root Test:
R =
- +∞, when lim n->+∞ (n-root|an|) = 0
- 0, when lim n->+∞ (n-root|an|) = +∞
- 1 / lim n->+∞ (n-root|an|), when lim n->+∞ (n-root|an|) = l in R
For R = +∞ the series converges for any real x.
For R = 0 the series diverges for any x in R except x0.
For the last one the Convergence Range is (x0 - R, x0 + R)
So, the convergence depends on the value of R and we have the following cases:
- R > 0 the series absolutely converges
- R = 0 the series converges only at the center x0 and diverges for any other real x
- R = +∞ the series converges absolutely for x in (x0 - R, x0 + R)
Differentiation and Integration of a Function:
Suppose S(an) is a powerseries that converges for any x in (x0 - R, x0 + R).
The function f(x) that is based on that powerseries is differentiable in the same range the series converges.
And so the derivative is:
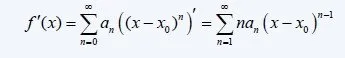
And f'(x) and the new Series we end up with convergence for the same radius R.
In the same we say that the function f(x) that is based on the series is integrable in the range [x0, x] or [x, x0] and so for any x in (x0 - R, x0 +R) we have that:
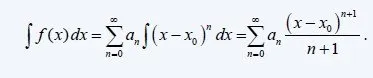
where the new Series and the Integral have the same Radius R as the given Series.
And this is actually it then!
How all this is useful will be discussed next time and I hope that everything till now seems interesting to follow along! So, get ready for the next post that will be even more interesting.
Bye!
