
Introduction
Hello it's a me again drifter1!
Continuing on with our Mathematical Analysis series of Mathematics we today will talk about Partial Derivatives.
Those "new" derivatives are based on the "normal" ones and so I highly suggest you reading my post about that here before getting into this post...if you don't know about them already!
So, without further do, let's get started!
What does a derivative describe?
When having only one variabe, the derivative of course describes the angle/rotation of a function's curve to the x axis.
So, the derivative of a function f(x) with x describes the angle towards the x-axis.
But, what about functions of more then one variables?
Well we saw that limits, continuity and more can also be described for such functions, but we don't talked about differentiation yet...
Depending on the notation the derivative at the position xo is given by:

using quicklatex
So, the derivatives are based on an specific quotient limit...
Partial Derivatives
Because we can clearly see that the "dependence" variable (x) is in the denominator we start thinking about a way of describing derivatives for one of the independent input variables. This exactly is what a partial derivative is.
For two variables we define the partial derivative of z = f(x, y) at the point P(x0, y0) with x as:
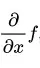 =
= 
Wikipedia and Quicklatex
If this limit exists (is a real number) then the value is called the partial derivative o f(x, y) with x at the point P(x0, y0).
By doing as we did, we actually define a new function f(x, y0) that is dependent only of x.
Using the same principle the derivative of f(x, y) with y is:

For example:

The Partial derivatives are:
f'x = 2x + 3y
f'y = -2y + 3x
We can clearly see that the "other" variable is being treated like a constant.
What does the partial derivative describe?
Well, it again describes the angle of a curve...
This curve will be different depending on which variable we choose to derivative with.
For the function f(x, y) at P(x0, y0) we have:
- f'x or the partial derivative with x at P describes the angle of f(x, y0)
- f'y or the partial derivative with y at P describe the angle of f(x0, y)
You can see that we find the angle of a new function g(x) or g(y) which means that we leave the 3-dimensions that a 2-variable functions describes to go to 2-dimensions (from plane to curve/line)
But, how can this be useful?
Derivative of Vector Functions
The derivative of a vector function is based on partial derivatives.
Suppose z = f(x, y) is a plane and r(t) = x(t)i + y(t)j a curve (or vector function) on top of it.
We define a derivative along the curve as:
f'(t) = df/dt = ∂f/∂x * dx/dt + ∂f/∂y * dy/dt
where these elements are:
- the partial derivative of x(t) with x AND
- the partial derivative of y(t) with y
But, because the functions are "complex" we have to use the rule of composition.
If we had 3-dimensions the derivative would look like this:
f'(t) = df/dt = ∂f/∂x * dx/dt + ∂f/∂y * dy/dt + ∂f/∂z* dz/dt
For example if r(t) = cost + sint and f(x, y) = x*y then:
f'(t) = df/dt = ∂f/∂x * dx/dt + ∂f/∂y * dy/dt = y*(-sint) + x*cost = -sin^2t + cos^2t
Partial Derivatives are also used for things like:
- Finding normal vectors to a plane
- Finding tangent planes
Both use directional derivatives that we will talk about next time...
And this is actually it for today and I hope that you enjoyed it!
Bye!
