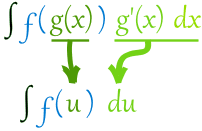
Hello its me again drifter1! Today we continue with Mathematical Analysis getting into our first Integration Technique! Last time in our first Integrals post (that you should check out first) I told you that I will talk about those techniques in parts so that we cover everything and get into good examples. Today's post will only be about the Substitution Technique that is used to solve many types of Integrals! So, without further do let's get started!
Substitution Introduction:
Suppose a function f: I -> R, that is continuous in I and x = g(t), where g is another function that is integratable in I' that is a subset of I.
If F is a antiderivative of f then:
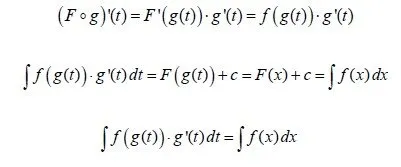
So, we can calculate the integral of function f by finding the integral of f(g(t))*g'(t). This means that we can substitute the independent variable x with g(t) so that we maybe simpify the first integral! We actually try to change an integral into some known form of those that we will cover later on or are basic integral forms that we already talked about last time.
Some important things about the substitute g(t):
- g(t) must be a 1-1 function, cause if G is a antiderivative of g then G(g^-1(t)) = F(x) that is the antiderivative of f.
- g(t) must be invertible and also integratable
- the choice for g(t) is not unique, but some work better then the other on specific cases
- we change the variable x with g(x) and also the new differential dt
- after calculating the integral for t we find the value for x by substituting t with g^1(x)
Example:
Suppose we want to calculate the integral of f(x) = 1 / xlnx .
Let's set t = lnx and so x = e^t = g(t).
We also need the new differential dt that we get by differentiating each side of lnx = t:
t'dt = (lnx)'dx => dt = 1/x dx .
So, our integral now can be solved easily like that:
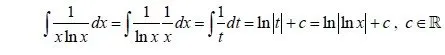
We simply set lnx = t and 1/x dx = dt and so we have a simple integral of 1/t that is ln|t| as a basic integral form. Setting t = lnx again we get our final answer ln|lnx| + c.
This was an pretty simply case that you can easily get by trying out different g(t) function on your own. Let's get into some more difficult cases, where the choice is not so obvious so that you can understand why and how we substitute so that we get a simpler integral that can be solved directly!
Integrals that contain root(a^2 - b^2*x^2) :
Set bx = a*sin(t), where a, b >0 and t in (-pi/2, pi/2).
Example:

We can see that we have root(2^2 - 1^2*x^2) at the denominator.
So, we set: x = 2sin(t) => x /2 = sin(t) => t = arcsin(x/2)
The differential is dx = 2cos(t)dt .
With x = 2sin(t) we have that:
root(4 - x^2) = root(4 - 4*sin^2(t)) = root(4*(1-sin^2(t))
This last bit is a basis trigonometric equation that gives us cos^2(t) and so:
root(4 - x^2) = root(4*cos^2(t)) = 2*cos(t), cause t is in (-pi/2, pi/2) where cos(t) > 0
That way our integral now looks like this:
integral [(4sin^2(t) / 2*cos(t))*2cos(t)dt] => 4*integral[sin^2(t)dt].
This last bit is also an trigonometric function that gives us (1 - cos(2t)) /2 and so:
4*integral[sin^2(t)dt] = 4*integral (1 - cos(2t)) /2)dt = 4*[1/2 integral(1dt) - 1/2 integral(cos(2t)dt)] =
2*(t - sin(2t)) + c = 2t - 2sin(2t) + c.
Let's also set t = arcsin(x/2) and so, our final result is;
2*arcsin(x/2) - 2*sin(2arcsin(x/2)) + c .
Integrals that contain root(b^2*x^2 - a^2) :
Don't confuse this one with the previous one!
Here we have to set bx = a*cosh(t), where a, b > 0 and t >= 0.
Example:
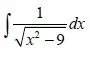
We can see that we have root(1^2*x^2 - 3^2) at the denominator.
So, we set x = 3*cosh(t) => x/3 = cosh(t) => t = arccosh(x/3) .
The differential is dx = 3*sinh(t)dt .
With x = 3cosh(t) we have:
root(x^2 - 9) = root(9*cosh^2(t) - 9) = root[9(cosh^2(t) - 1)].
From hyberbolic trigonometry we know that cosh^2(t) - sinh^2(t) = 1 and so:
root(x^2 - 0) = root(9sinh^2(t) = 3sinh(t).
That way our integral now looks like this:
integral [3sinh(t) dt / 3sinh(t)] = integral 1dt = t + c.
Setting t = arccosh(x/3) we have our final result: arccosh(x/3) + c .
Integrals that contain root(a^2*x^2 + b^2) :
When we have a addition we can directly identify this case.
Here we can set ax = b*sinh(t) or ax = btan(t), where a, b > 0
The second one is also used in cases where a^2*x^2 + b^2 is not in a root!
Example:

Here we can not directly see that this is such a case.
If we take 4x^2 + 4x + 1 we know that this equals (2x + 1)^2 and so:
4x^2 + 4x + 5 = (2x+1)^2 + 4 = (2x+1)^2 + 2^2 that is what we want!
So, we set 2x+1 = 2*sinh(t) => t = arcsinh(2x+1 / 2)
The differential is d(2x+1) = d(2sinh(t)) => dx = cosh(t)dt
Let's set (2x+1)^2 = 4sinh^2(t). We have that:
root((2x+1)^2 + 4) = root(4sinh^2(t) + 4) = root(4(sinh^2(t) +1)).
Which again is the same hyberbolic trigonometric equation and so we get:
root(4cosh^2(t)) = 2cosh(t).
So, our integral now becomes:
integral (2cosh(t) * cosh(t)dt) = 2*integral(cosh^2(t)dt)
This last one can be analyzed as an trigonometric equation that gives us 1+ cosh(2t) / 2 .
So, 2*integral( 1+ cosh(2t) / 2)dt = 2*[1/2 integral(1dt) + 1/2 integral cosh(2t)dt] = t + 1/2 sinh(2t) + c .
If we know set t = arcsinh(2x+1 / 2) we get our final result:
arcsinh(2x+1 / 2)+ 1/2 sinh(2*arcsinh(2x+1 / 2)) + c .
In this case the substituting with the "ax = btan(t)" would actually make it more difficult, but sometimes this one might be easier and of course we use the second one always when there is no root!
These are actually the most common types of substitution. In any other case of roots we simply set the sub-root part or the whole root equal to t and execute the same procedure. So, any time you see a integral that contains something that you can't find directly and easily, you can try setting it equal to some substitute function to see if this part goes away. If you look at all of my examples/cases today, you can see that we try to make basic integrals out of the ones that are more complicated!
And this is actually it for today and I hope that you enjoyed it!
The next technique that I will cover in our series is the so called "Integration by Parts" Technique that is very popular and mostly simple, but can get a little difficult if you have composition functions.
Bye!
