Hello its a me again drifter1. Today we continue with Mathematical Analysis getting into Fourier Series. You should check out my post about Power Series first here. So, without further do, let's get straight into it!
Getting into Fourier Series:
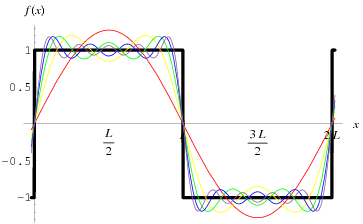
Using the knowledge from Power Series and to solve problems of Mathematics and Physics even faster we created a trigonometric polynomial Series that consists only of sin(nx) and cos(nx) terms called a Fourier Series. Using this series we can calculate an approximate value for an periodic function f, when n goes to infinity.
An trigonometric polynomial of k-degree looks like this:

where an, bn are coefficients and x is a real number.
The minimim value Tn for which:
sin(n(x+Tn)) = sin(nx) AND cos(n(x+Tn)) = cos(nx)
is called the period of the functions sin(nx) and cos(nx) for every natural number n.
This value can be found using the equation:
Tn = 2π / n
The series we get from the upper polynomial when k -> ∞ looks like this:

where a0, an, bn and n are constant natural numbers and x is a real variable.
So, now the questions are:
- how we calculate those coefficients a0, an, bn?
- when does the series converge?
For the second one its been proven that we simply have to check if the series of (|an| + |bn|) terms converges and when it converges. Cause, we can use the absolute convergence criterion.
We can rewrite the function in that way:

If we now integrate this function in the range [0, 2π] we end up with:

This equation lets us calculate the value of a0.
By doing some trigonometric integrations of sin(nx) + cos(mx) etc. we can end up with two equations that will help us calculate the values of an, bn. I will not get into how we find them, but I think it actually is not that important to know how we end up with those. It's more important to know them, because they are useful.
So, those equations are:
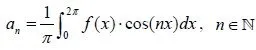

So, if f is an integrable function in the range [0, 2π]. The Fourier Series of f is the trigonometric series we talked about and we calculate the value of the coefficients using the equations above.
Generalization for every function:
If the function is integrable in the range [-a, a] with a>0 then the fourier series looks like that:

and we calculate the values of the coefficients using the following equations:

Here you can see some Examples and read about more things that have to do with Fourier Series.
We will off course get back to them later on when we get into Signals...
And this is actually it! I hope you enjoyed it!
Because of Christmas Eve I may not upload so frequently for some days now, but I plan to upload Graph Algorithms in Java again!
Bye!
