Introduction
Hello it's a me again drifter1!
Today, we will continue with our Mathematical Analysis series of Mathematics by getting into Directional Derivatives that are based on Partial Derivatives that we covered last time.
As I already said last time, Directional Derivatives are used for finding normal vectors to a plane and also for finding tangent planes.
There is not much more to say about, so let's get started!
Small recap
Last time we talked about Derivatives of vector functions (curves) on top of planes.
If z = f(x, y) and r(t) = x(t)i + y(t)j then the derivative along the curve is given by:
f '(t) = df/dt = ∂f/∂x * dx/dt + ∂f/∂y * dy/dt
We can see that we use the rule of composition, because those functions are "complex".
The function f(x, y) is a function of x and y, but x(t) and y(t) are functions of t. This means that we first partially differentiate f(x, y) by x or y and multiply this with the derivative of x(t) or y(t) with t.
Of course the derivative along a curve can also be found for 3 or even more dimensions...
Tangent vectors
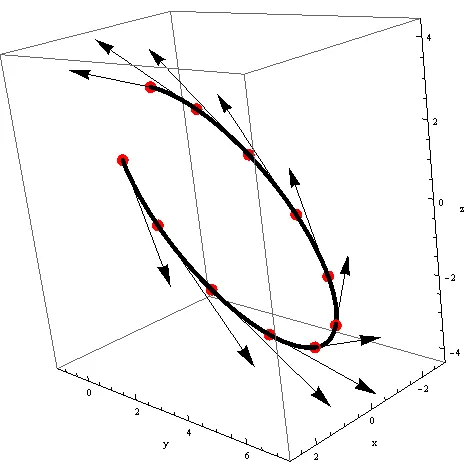
Suppose the plane f(x, y, z) = c and the curve r(t) = x(t)i + y(t)j + z(t)k.
The derivative along the curve is:
u = df/dt = ∂f/∂x * dx/dt + ∂f/∂y * dy/dt + ∂f/∂z* dz/dt
The tangent vector of the curve r is:
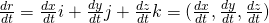
The gradient of f (or Del of f) is the vector:
∇f = gradf = (∂f/∂x, ∂f/∂y, ∂f/∂z)
So, the derivative along the curve is:
df/dt = (∂f/∂x, ∂f/∂y, ∂f/∂z) * (dx/dt, dy/dt, dz/dt) = ∇f * u
where ∇f is the gradient of f and u is a tangent vector of curve r(t) = (x(t), y(t), z(t))
If u =(a, b, c) is a unit vector (|u| = 1) and P0 a Point in space then:
∇f(P0) * u = Duf(P0)
is called the derivative of f along the direction of u = (a, b, c).
For example:
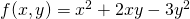

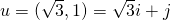
Duf(P) = ?
The given vector u is not an unit vector and so we have to convert it.

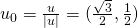
The gradient of f is:
∇f = (∂f/∂x, ∂f/∂y) = (2x + 2y, 2x - 6y)
For the point P we have:
∇f(P) = (1 + 1, 1 - 3) = (2, -2)
That way:
Duf(P0) = ∇f(P) * u0 =>
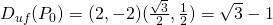
Some equations through quicklatex.
An explanation
Suppose we have the same plane and curve as before, the unit vector u = (u1, u2, u3) and the Point P0(x0, y0, z0).
And ε is a line that passes through P0, is parallel to u and has the parametric equations:
x = x0 + u1t
y = y0 + u2t
z = z0 + u3t
Then dx/dt = u1, dy/dt = u2, dz/dt = u3 and so:
df/dt = ∇f(P0) * (u1, u2, u3) = ∇f(P0) * u = Duf(P0)
Which of course is the derivative of f along the direction of u.
Some interesting cases
We can write the same equation like that:
Duf(P0) = ∇f(P0) * u = |∇f(P0) ||u|*cosφ
where φ is the angle between the vectors ∇f(P0) and u.
This is clearly a "dot" product between vectors...
Depending on the angle we have the following cases:
- φ = 0, ∇f(P0) and u are parallel => Duf(P0) = |∇f(P0)| (highest possible increase of f)
- φ = π, ∇f(P0) = -u => Duf(P0) = -|∇f(P0)| (highest possible decrease of f)
- φ = π/2, ∇f(P0) and u are across and so Duf(P0) = 0
And so:
-|∇f(P0)| <= Duf(P0) <= |∇f(P0)|
Normal vectors to a plane
So, now after all that we can finally get into the actual useful thing of this post...
Suppose S: f(x, y , z) = c being a plane/surface and r(t) = x(t)i + y(t)j +z(t)k a curve on top of it that passes through the point P0(x0, y0, z0).
u = dr/dt = (dx/dt, dy/dt, dz/dt) is a tangent vector of curve r at P0.
Let's also suppose N = (a, b, c) being a normal vector to our plane.
Of course we can find a ∇f(P0) so that:
∇f(P0) * u = 0, which means that they are vertically across..
So, N = ∇f(P0)
Tangent planes
By using this concept, planes/surfaces of the form:
a(x - x0) + b(y- y0) + c(z - z0) = 0
have N = (a, b, c) as a normal vector and also pass through P0.
So, with f(x, y, z) = c being a plane and P0(x0, y0, z0) a point,
the equation of a tangent plane is:
∂f/∂x (x - x0) + ∂f/∂y (y - y0) + ∂f/∂z (z - z0) = 0
For a surface f(x, y) = z we have:
F(x, y, z) = f(x, y) - z = 0
And so;
∂F/∂x = ∂f/∂x
∂F/∂y = ∂f/∂y
∂F/∂z = -1
Which means that:
N = ∇f(P0) = (∂f/∂x, ∂f/∂y, -1)
And finally the equation of such a tangent plane is:
∂f/∂x (x - x0) + ∂f/∂y (y - y0) - (z - z0) = 0
And this is actually it for today and I hope that you enjoyed it!
Next time we will start getting into double/surface integrals!
Bye!
